基础算法-整数二分

基本思想——折半
二分法的基本思想比较简单，是用来在数组当中查找特定元素的算法。
二分可以分为整数二分和浮点二分，本文主要介绍整数二分。

具体步骤

首先，从数组的中间元素开始搜索，如果该元素恰好是目标元素，则搜索过程结束，否则继续执行。
如果目标元素大于/小于中间元素，则在数组大于/小于中间元素的那一半区域查找，然后重复上一步的操作。
如果某一步数组为空，则表示找不到目标元素。
边界更新的两种方式

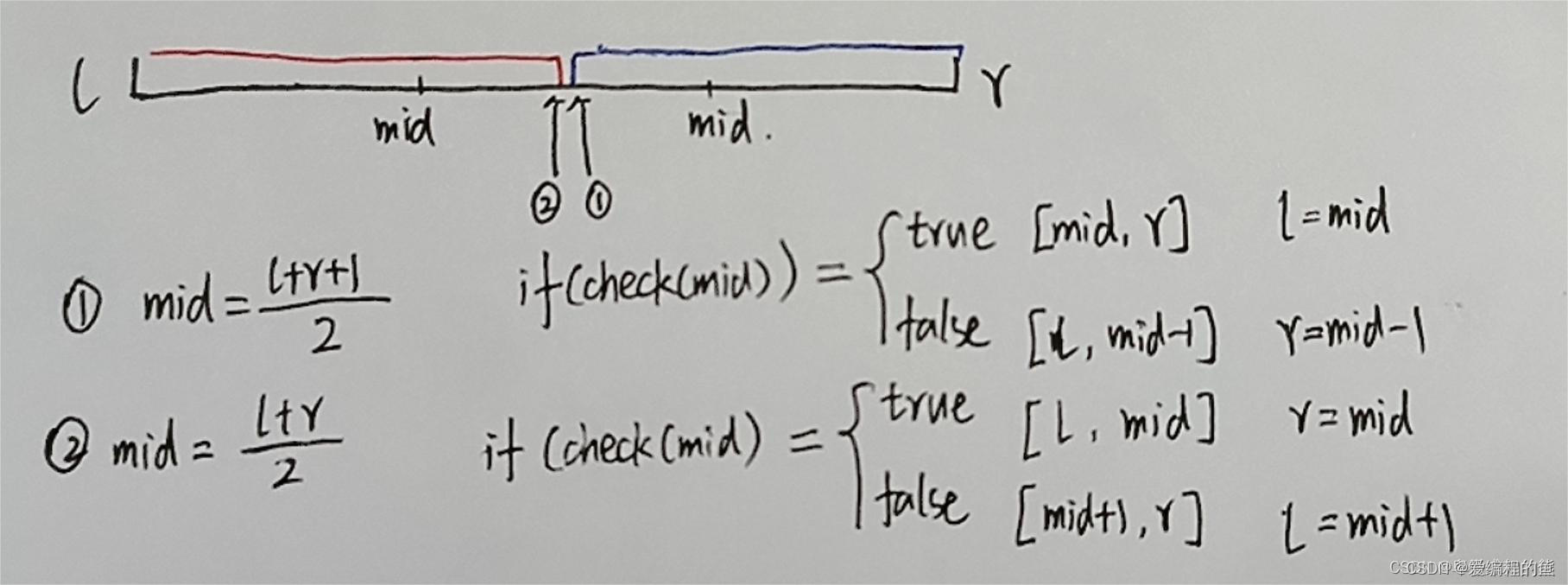
当 mid=l+r+1>>1 时，查找值指向箭头2位置，检查 mid 是否满足红色部分性质，如果成立的话，mid 便在红色区域当中，此时，查找值便在区域 [mid，r] 里面，此时更新边界的方法为 l=mid 。如果不成立的话，mid 便在蓝色区域当中，此时查找值便在区域 [l，mid-1] 里面，此时更新边界的方法为 r=mid-1 。
当 mid=l+r>>1 时，查找值指向箭头1位置，检查 mid 是否满足蓝色部分性质，如果成立的话，mid 便在蓝色区域当中，此时，查找值便在区域 [l，mid] 里面，这里要注意包含边界，因为我们的查找值可能就是边界，此时更新边界的方法为 r=mid 。如果不成立的话，mid 便在红色区域当中，此时查找值便在区域 [mid，r] 里面，此时更新边界的方法为 l=mid+1 。

注意事项

二分法特别需要注意左右两端的边界问题，如果发生问题绝大部分都是由边界产生的，因此本文提供三种模板来应对不同情况下的二分问题。
单调性与二分法并没有直接关系。如果题目具有单调性的话我一定可以使用二分法，但是我可以使用二分法的题目不一定非得由单调性。
C++ 整数除法是 向下取整。

题目描述

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。
对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。
如果数组中不存在该元素，则返回 -1 -1。

输入格式
第一行包含整数 n 和 q，表示数组长度和询问个数。
第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。
接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式
共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回 -1 -1。

数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例
6 3
1 2 2 3 3 4
3
4
5

输出样例
3 4
5 5
-1 -1

实现方法

1. 方法一（模板）

#include <bits/stdc++.h>
using namespace std;

const int N=100000;
int n,m; 
int q[N];
int main()
{
    cin>>n>>m;
    for (int i = 0; i < n; i ++ )
    {
        cin>>q[i];
    }
    while (m -- )
    {
        int x;
        cin>>x;

        int l = 0, r = n - 1;
        while (l < r)
        {
            int mid = l + r >> 1;
            if (q[mid] >= x)
            {
                r = mid;
            }
            else
            {
                l = mid + 1;
            }
        }
        if (q[l] != x)
        {
            cout << "-1 -1" << endl;
        }
        else
        {
            cout << l << ' ';
            int l = 0, r = n - 1;
            while (l < r)
            {
                int mid = l + r + 1 >> 1;
                if (q[mid] <= x)
                {
                    l = mid;
                }
                else
                {
                    r = mid - 1;
                }
            }
            cout << l << endl;
        }
    }
    system("pause");
    return 0;
}

2. 方法二（不需要考虑边界）

详细思路请见 B站up主五点七边视频

#include <bits/stdc++.h>
using namespace std;

const int N=100000;
int n,m; 
int q[N];
int left_border(int x)
{
    int l = -1, r = n;
    while (l + 1 != r)
    {
        int mid = (l + r) >> 1;
        if (x > q[mid]) l = mid;
        else r = mid;
    }

    if (r == n || q[r] != x)
    {
        return -1;
    }
    else
    {
        return  r;
    }
}
int right_border(int x)
{
    int l = -1, r = n;
    while (l + 1 != r)
    {
        int mid = (l + r) >> 1;
        if (x < q[mid])
        {
            r = mid;
        }
        else 
        {
            l = mid;
        }
    }

    if (l == -1 || q[l] != x)
    {
        return -1;
    }
    else
    {
        return l;
    }
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
    {
        cin >> q[i];
    }
    while (m--)
    {
        int x;
        cin>>x;
        cout<<left_border(x)<<" "<<right_border(x)<<endl;
    }
    system("pause");
    return 0;
}

3. 方法三（调用函数）

函数解释

binary_search(arr[], arr[]+size, index) 查找某个元素是否出现
lower_bound(arr[], arr[]+size, index) 查找第一个大于或等于某个元素的位置
upper_bound(arr[] , arr[]+size, index) 查找第一个大于某个元素的位置
注解：arr[]:数组首地址，size:数组元素个数，index：需要查找的值
 

#include <bits/stdc++.h>
using namespace std;

const int N=100000;
int n,m; 
int q[N];
int main()
{
    cin >> n >> m;
    for(int i = 0;i < n;i++)
    {
        cin >> q[i];
    }
    while(m--)
    {
        int x;
        cin >> x;
        if(binary_search(q,q+n,x))
        {
            cout << lower_bound(q,q+n,x) - q << " " 
            << upper_bound(q,q+n,x) - q - 1 << endl;
        }else{
            cout << "-1 -1" << endl;
        }
    }
    return 0;
}