文章目录
- 前言
- T1.36进制加法(模拟)
- 题面
- 思路
- 代码
- T2.电影院选座(DFS)
- 题面
- 思路
- 代码
- T3.IP地址(DFS)
- 题面
- 思路
- 代码
前言
前段时间🐏了,今天简单写了一下,不知道如何提交代码进行评测,题目比较简单,不过我也有可能写错,但是大体思路应该就是这样了,有问题可以在评论区指出,看到后我会积极改正的~
活动地址:https://juejin.cn/post/7171281973527838751
T1.36进制加法(模拟)
题面
题目链接:https://code.juejin.cn/pen/7180199398167543867

思路
思路比较简单,我们先用两个string来存储相加的两个字符串,然后将其转化为十进制数字,倒叙放入vector中(方便后续加法的进位),然后就是简单的进位加法了,注意的是这里进位的时候可能会让整体长度加一,于是我们先给较长的数值加一个前置0,这样就不会发生越界了
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
const ll base = 36;
ll trans_int36(char c) {
if(c >= '0' && c <= '9') return int(c - '0');
else return int(c-'a' + 10);
}
char trans_char36(ll c) {
if(c <= 9) return int('0' + c);
else return char('a' + (c - 10));
}
void add_vector(vector<int> &a, vector<int> &b) {
for(int i = 0,len = b.size();i < len; ++i) {
a[i] += b[i];
a[i + 1] += a[i] / base;
a[i] %= base;
}
for(int i = b.size(),len = a.size();i < len - 1; ++i) {
a[i + 1] += a[i] / base;
a[i] %= base;
}
if(a.size() > 1 && a[a.size() - 1] == 0) a.pop_back();
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
vector<int> a,b;
string sa,sb;
cin>>sa>>sb;
for(int i = sa.size()-1;i >= 0; --i) {
a.push_back(trans_int36(sa[i]));
}
for(int i = sb.size()-1;i >= 0; --i) {
b.push_back(trans_int36(sb[i]));
}
if(a.size() < b.size()) swap(a,b);
a.push_back(0);
add_vector(a,b);
for(int i = a.size() - 1; i >= 0; --i) {
cout<<trans_char36(a[i]);
}
cout<<endl;
return 0;
}
/*
input:
abbbb 1
output:
abbbc
*/
T2.电影院选座(DFS)
题面
题目链接:https://code.juejin.cn/pen/7180200444763832354
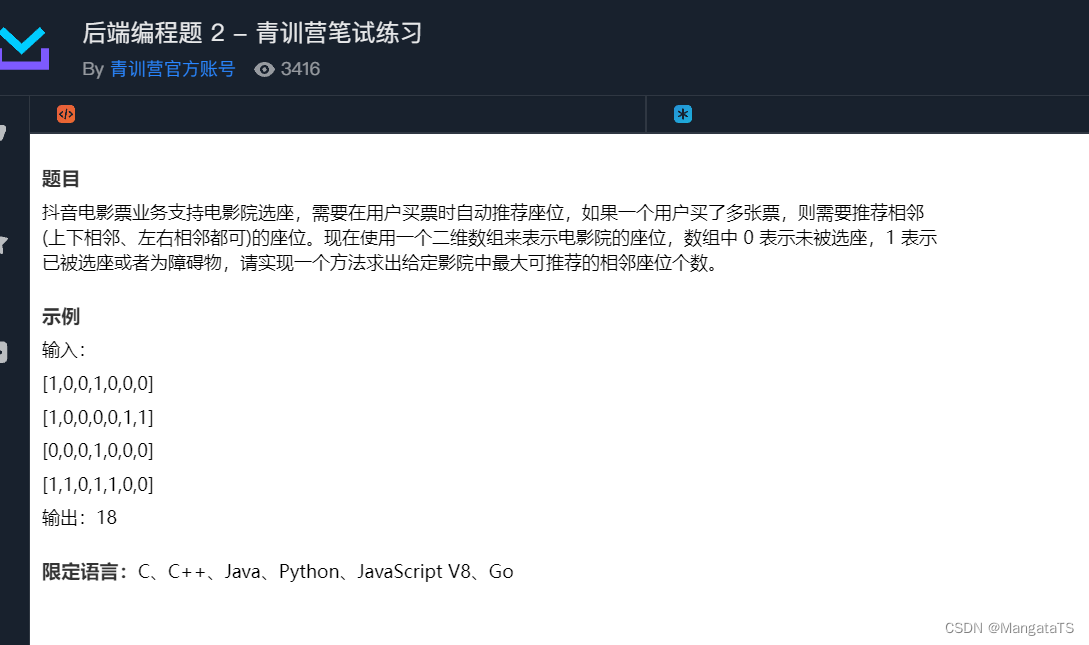
思路
一个很简单的图的连通问题,我们只需要找到最大的连通块就行,思路很多种,最简单的就是写一个DFS,只要找到空闲的位置,我们就从这个点开始搜索,并且在搜索的过程中记录这个连通块的大小,最后更新一下ans值
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
const int N = 1e3+10;
int n,m,cnt;
int dx[4]={1,-1,0,0},dy[4]={0,0,-1,1};
bool mp[N][N];
void dfs(int i,int j) {
if(i < 0 || j < 0 || i >= n || j >= m) return;
if(mp[i][j]) return;
cnt++;
mp[i][j] = true;
for(int k = 0;k < 4; ++k) {
int nx = i + dx[k];
int ny = j + dy[k];
dfs(nx,ny);
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
cin>>n>>m;
for(int i = 0;i < n; ++i)
for(int j = 0;j < m; ++j)
cin>>mp[i][j];
for(int i = 0;i < n; ++i)
for(int j = 0;j < m; ++j)
cout<<mp[i][j]<<" \n"[j == m-1];
int ans = 0;
for(int i = 0;i < n; ++i)
for(int j = 0;j < m; ++j) {
if(!mp[i][j]) {
cnt = 0;
dfs(i,j);
ans = max(ans,cnt);
}
}
cout<<ans<<endl;
return 0;
}
/*
input:
4 7
1 0 0 1 0 0 0
1 0 0 0 0 1 1
0 0 0 1 0 0 0
1 1 0 1 1 0 0
output:
18
input:
4 7
1 0 0 1 0 0 0
1 1 1 1 0 1 1
0 0 0 1 0 0 0
1 1 0 1 1 0 0
output:
9
*/
T3.IP地址(DFS)
题面
题目链接:https://code.juejin.cn/pen/7180201853819781157
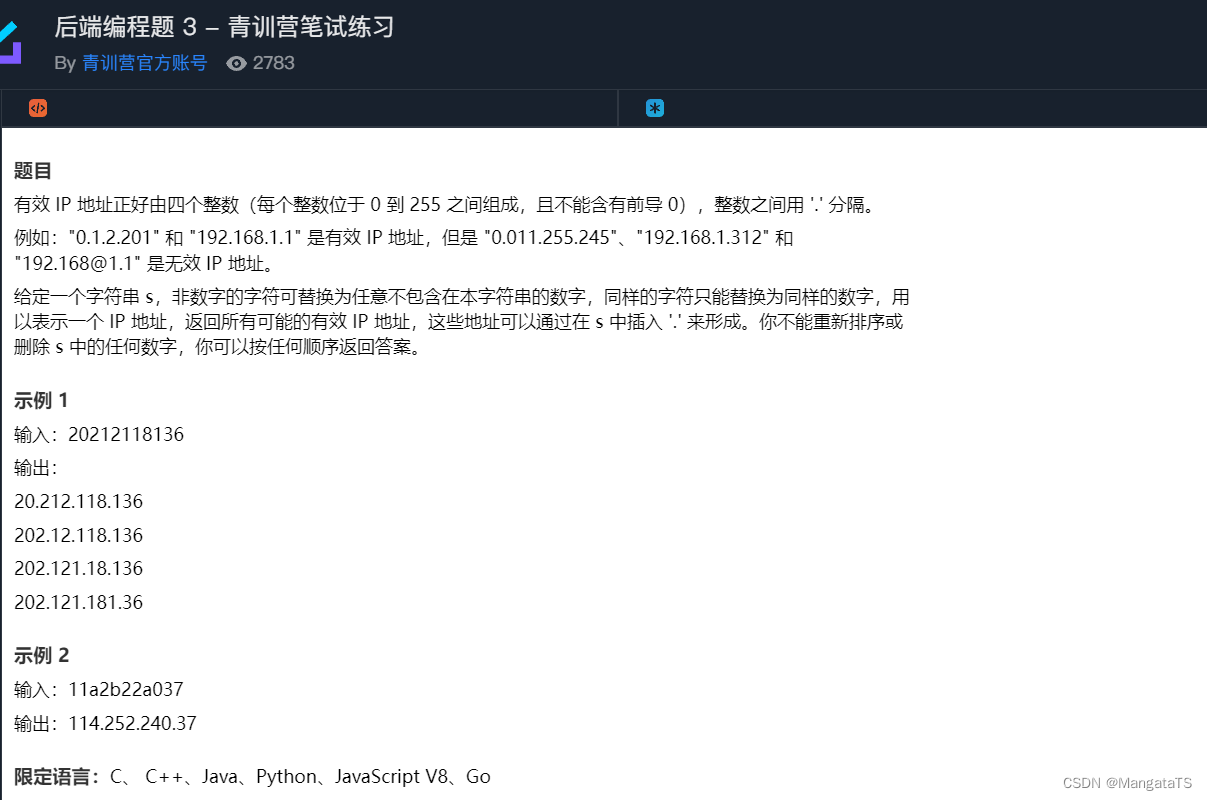
思路
思路比较简单,不过数据处理起来有一点麻烦
-
首先这一串可以看作数字和非数字组成,对于非数字部分,我们需要替换成字符串中未出现的数字,并且重复的字母表示同一个数字,那么我们就处理这个非数字字母和数字的对应关系就好了,那么这个就可以用回溯搜索来匹配这个关系,我们每一层搜索就确定一个字母和一个数字的匹配,然后搜索的出口就是将所有出现的字母与数字匹配完成(当然也有可能不存在字母,那就直接进行检查环节)
-
匹配完成后就是将对应的字母替换成数字,然后取校验这个数字是否合法,比如不能存在前导 0 0 0 ,不能大于 255 255 255 ,因为
ip地址是一个四位的值,那么我们一一校验即可,如果满足条件,那么我们就直接输出这个结果即可 -
然后还有个问题就是断点,其实我们就可以想象成
.在字符串中放置的方法,其实就是一个三重循环即可,.是不能放在最左边和最右边的,那么其位置的范围就是第一个字符的右边到,倒数第二个字符的右边,我这里就是将i表示的含义就是将.放在第i个字符的右边,j、k也是如此,那么这个问题到这里就结束了
代码
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define endl "\n"
bool vis[10];
map<char,int> mp;
set<char> st;
vector<char> vec;
int vec_len;
string sa[4],sb[4];
bool check(string ss) {
if(ss[0] == '0' && ss.size() != 1) return false;
int kk = 0;
for(int i = 0;i < ss.size(); ++i) {
if(ss[i] < '0' || ss[i] > '9') return false;
kk = kk * 10 + (ss[i] - '0');
}
if(kk > 255 || kk < 0) return false;
return true;
}
void dfs(int loci) {
if(loci == vec_len) {
for(int i = 0;i < 4; ++i) {
for(int j = 0,loc_len = sa[i].size();j < loc_len; ++j) {
if(sa[i][j] >= '0' && sa[i][j] <= '9')
sb[i][j] = sa[i][j];
else {
if(mp[sa[i][j]] < 0 || mp[sa[i][j]] > 9)
return;
sb[i][j] = char(mp[sa[i][j]] + '0');
}
}
if(check(sb[i]) == false) return;
}
string loc_ss = sb[0];
for(int i = 1;i < 4; ++i) {
loc_ss.append(".");
loc_ss.append(sb[i]);
}
cout<<loc_ss<<endl;
return;
}
for(int i = 0; i <= 9; ++i) {
if(vis[i]) continue;
mp[vec[loci]] = i;
vis[i] = true;
dfs(loci + 1);
vis[i] = false;
mp[vec[loci]] = -1;
}
}
int main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
string ss;
cin>>ss;
int len = ss.size();
if(len < 4 || len > 12) return 0;//no answer
for(int i = 0;i < len; ++i)
if(ss[i] >= '0' && ss[i]<= '9')
vis[ss[i]-'0'] = true;
else
st.insert(ss[i]);
for(auto it : st)
vec.push_back(it);
vec_len = vec.size();
for(int i = 0; i < len-1; ++i) {
for(int j = i + 1;j < len-1; ++j) {
for(int k = j + 1 ;k < len - 1; ++k) {
sa[0] = ss.substr(0,i + 1);
sa[1] = ss.substr(i + 1,j - i);
sa[2] = ss.substr(j + 1,k - j);
sa[3] = ss.substr(k + 1,len-k-1);
for(int l = 0;l < vec_len; ++l)
mp[vec[l]] = -1;
for(int l = 0;l < 4; ++l) {
sb[l] = sa[l];
}
dfs(0);
}
}
}
return 0;
}
/*
input1:
11a2b22a037
output1:
114.252.240.37
115.242.250.37
input2:
20212118136
output2:
20.212.118.136
202.12.118.136
202.121.18.136
202.121.181.36
*/