数据结构_红黑树(C语言)

news2025/1/11 20:58:45

数据结构总目录

红黑树

介绍：

  • 红黑树是一种特化的AVL树（平衡二叉树），都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。
  • 红黑树是一种平衡二叉查找树的变体，它的左右子树高差有可能大于 1，所以红黑树不是严格意义上的平衡二叉树（AVL），但 对之进行平衡的代价较低， 其平均统计性能要强于 AVL
  • 由于每一棵红黑树都是一颗二叉排序树，因此，在对红黑树进行查找时，可以采用运用于普通二叉排序树上的查找算法，在查找过程中不需要颜色信息

1. 图文解析

红黑树性质

  • 性质一：结点是红色或黑色
  • 性质二：根结点是黑色
  • 性质三：空结点为叶子结点，且所有叶子结点都是黑色
  • 性质四：每个红色结点的两个子结点都是黑色
  • 性质五：从任一结点到其每个叶子的所有路径都包含相同数目的黑色结点

1.1 存储结构

与一般二叉树相比，红黑树的结构存在父结点指针和结点颜色的标识

typedef char DataType;

typedef struct RBNode
{
    int color;                      // 结点颜色（0:黑色  1:红色）
    DataType data;                  // 结点数据
    struct RBNode *parent;          // 父结点指针，用于定位
    struct RBNode *lchild, *rchild; // 左右孩子指针
}RBNode, *RBTree;

1.2 红黑树的插入操作

在红黑树的插入时，第一个问题就是新插入的结点应该为红色还是黑色呢？

  • 根据性质二：如果初始红黑树为空，则插入的一定是根节点且为黑色
  • 根据性质五：如果新插入的结点为黑色，那么势必会导致路径上的黑色结点数量的增加，无疑增加了插入后的调整难度
  • 根据性质三：如果新插入的结点为红色，那么新结点的两个空结点一定为黑色，那么就不会增加路径上的黑色结点数量

总结：若插入的是根结点，则设置为黑色，其他情况则设置为红色

已知新插入的结点为红色，而如果父结点也为红色，就会违反性质四，则说明此时需要调整红黑树
同时在父亲结点为红色的条件下，则根据性质二，父亲结点一定不是根结点，且存在祖父结点

调整情况如下：

若父亲结点为祖父结点的左孩子结点

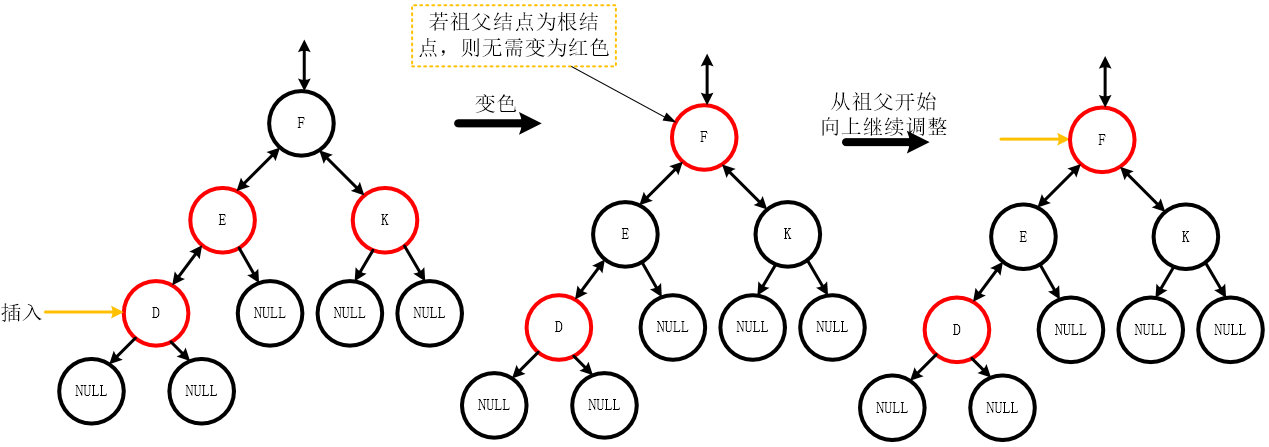
  1. 叔叔结点为红色
    调整过程：父亲结点和叔叔结点均变为红色，祖父结点若不是根结点，则变为红色，并将祖父结点视为新插入的结点，继续向上调整

在这里插入图片描述

  1. 叔叔结点为黑色

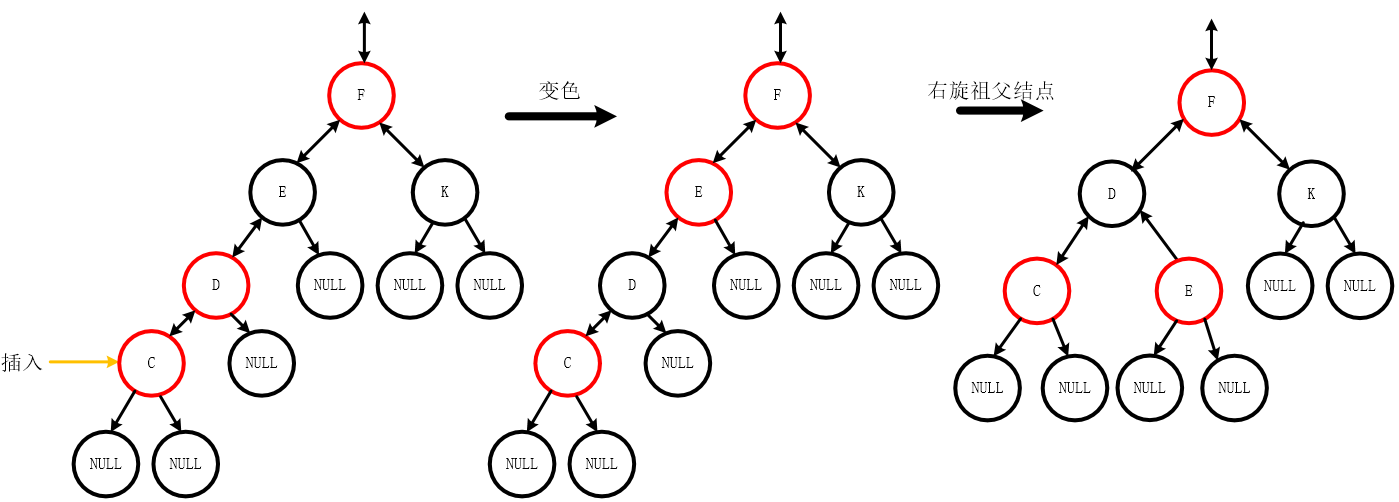
2.1 插入的位置是父亲结点的左孩子

  • 调整过程：父亲结点变为黑色，祖父结点变为红色，最后右旋祖父结点

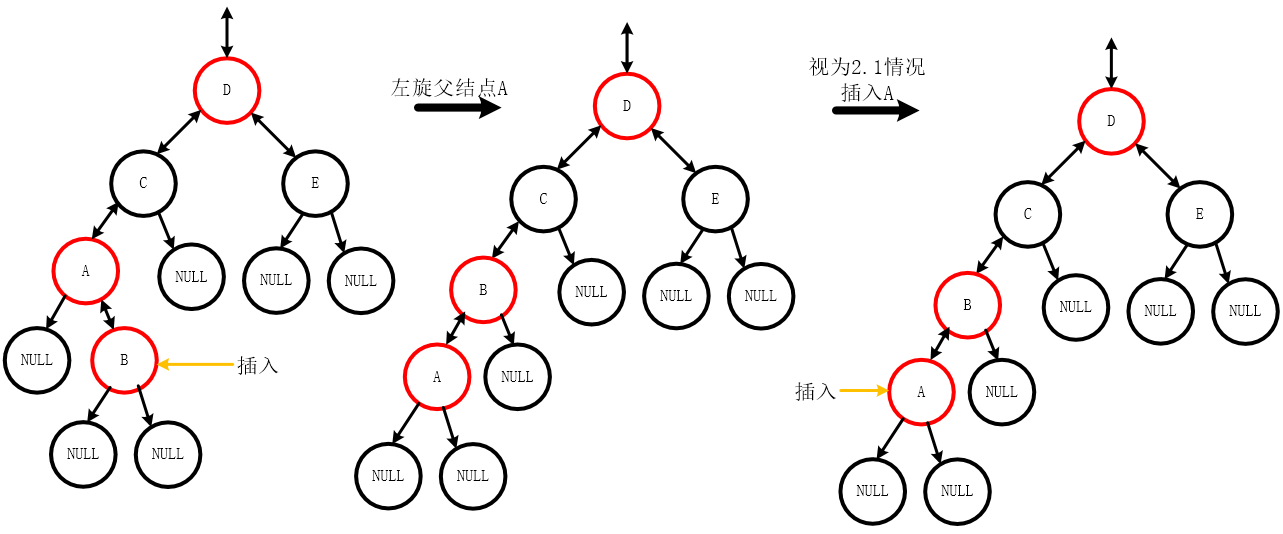
在这里插入图片描述

2.2 插入父亲结点的右孩子

  • 调整过程：左旋父结点，而后可视为2.1的情况进行调整

在这里插入图片描述

若父亲结点为祖父结点的右孩子结点，其操作与以上情况对称，详细见代码

2. 源代码

#include<stdio.h>
#include<stdlib.h>

typedef char DataType;

typedef struct RBNode
{
    int color;                      // 结点颜色（0:黑色  1:红色）
    DataType data;                  // 结点数据
    struct RBNode *parent;          // 父结点指针，用于定位
    struct RBNode *lchild, *rchild; // 左右孩子指针
}RBNode, *RBTree;

void InitRBTree(RBTree *T)
{
    (*T) = NULL;
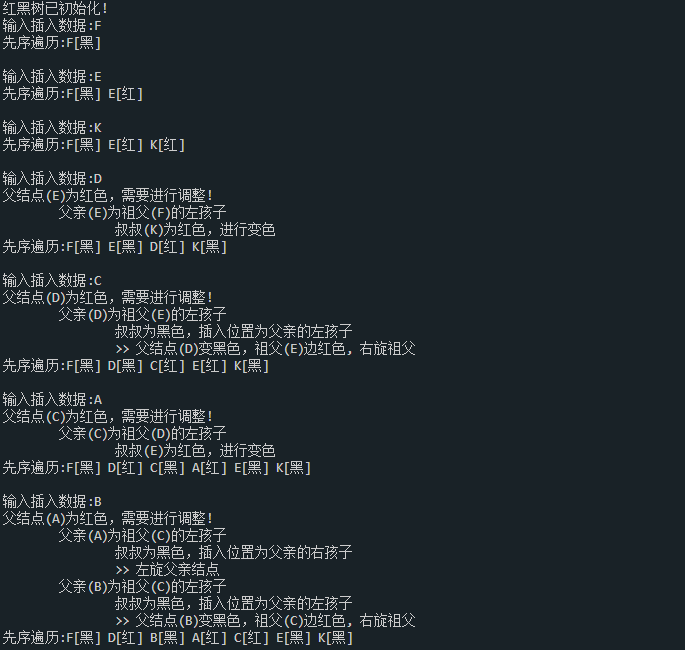
    printf("红黑树已初始化!\n");
}

// 创建新结点
RBNode *NewNode(int color, DataType x)
{
    RBNode *newNode;
    newNode = (RBNode *)malloc(sizeof(RBNode));
    newNode->data = x;
    newNode->color = color;    
    newNode->parent = newNode->lchild = newNode->rchild = NULL;
    return newNode;
}

// 右旋转， 
void RightRotate(RBNode *node, int flag)
{
    RBNode *parent = node->parent;
    RBNode *left = node->lchild;

    node->lchild = left->rchild;
    if (left->rchild)
    {
        left->rchild->parent = node;
    }
    
    left->rchild = node;
    node->parent = left;

    left->parent = parent;
    if (parent)
    {
        // flag = 0：node为父结点左孩子
        // flag = 1：node为父结点右孩子
        !flag ? (parent->lchild = left) : (parent->rchild = left);
    }
}

// 左旋转
void LeftRotate(RBNode *node, int flag)
{
    RBNode *parent = node->parent;
    RBNode *right = node->rchild;
    
    node->rchild = right->lchild;
    if (right->lchild)
    {
        right->lchild->parent = node;
    }
    
    right->lchild = node;
    node->parent = right;

    right->parent = parent;
    if (parent)
    {
        // flag = 0：node为父结点左孩子
        // flag = 1：node为父结点右孩子
        !flag ? (parent->lchild = right) : (parent->rchild = right);
    }
}


// 红黑树调整
void RBTreeAdjust(RBNode *node)
{
    // 父结点为红色，则父结点一定不是根结点，且祖父结点一定存在
    RBNode *father = node->parent;
    RBNode *grandfather = father->parent;
    RBNode *uncle;

    if (father && father == grandfather->lchild)
    {
        // 父亲为祖父的左孩子
        uncle = grandfather->rchild;
        // printf("\t父亲(%c)为祖父(%c)的左孩子\n", father->data, grandfather->data);
        if (uncle && uncle->color == 1)
        {
            // 若叔叔结点存在且为红色，则进行变色
            // printf("\t\t叔叔(%c)为红色，进行变色\n", uncle->data);
            father->color = 0;
            uncle->color = 0;
            grandfather->color = 1;
            // 递归调整祖父结点
            if (grandfather->parent && grandfather->parent->color == 1)
            {
                RBTreeAdjust(grandfather);
            }
            else if(!grandfather->parent)
            {
                grandfather->color = 0;
            }
        }
        // 叔叔结点不存在，或者为黑色
        else if (node == father->lchild)
        {
            // 若插入的结点是父亲的左孩子，则进行变色并对祖父进行右旋转
            // printf("\t\t叔叔为黑色，插入位置为父亲的左孩子\n");
            // printf("\t\t>> 父结点(%c)变黑色，祖父(%c)边红色, 右旋祖父\n", father->data, grandfather->data);

            father->color = 0;
            grandfather->color = 1;
            RightRotate(grandfather, 0);
        }
        else
        {
            // 若插入的结点是父亲的右孩子，则对父亲进行左旋转
            // printf("\t\t叔叔为黑色，插入位置为父亲的右孩子\n");
            // printf("\t\t>> 左旋父亲结点\n");
            
            LeftRotate(father, 0);
            RBTreeAdjust(father);
        }
    }
    else
    {
        // 父亲为祖父的右孩子
        uncle = grandfather->lchild;
        // printf("\t父亲(%c)为祖父(%c)的右孩子\n", father->data, grandfather->data);

        // 以下同理，对称操作
        if (uncle && uncle->color == 1)
        {
            // printf("\t\t叔叔(%c)为红色\n", uncle->data);
            father->color = 0;
            uncle->color = 0;
            grandfather->color = 1;
            // 递归调整祖父结点
            if (grandfather->parent && grandfather->parent->color == 1)
            {
                RBTreeAdjust(grandfather);
            }
            else  if(!grandfather->parent)
            {
                grandfather->color = 0;
            }
        }
        else if (node == father->lchild)
        {
            // printf("\t\t叔叔为黑色，插入位置为父亲的左孩子\n");
            // printf("\t\t>> 右旋父亲结点\n");

            RightRotate(father, 1);
            RBTreeAdjust(father);
            
        }
        else
        {
            // printf("\t\t叔叔为黑色，插入位置为父亲的右孩子\n");
            // printf("\t\t>> 父结点(%c)变黑色，祖父(%c)边红色, 左旋祖父\n", father->data, grandfather->data);

            father->color = 0;
            grandfather->color = 1;
            LeftRotate(grandfather, 1);
        }
    }
}

// 插入
void RBTreeInsert(RBTree *T, DataType x)
{
    // 若树为空，则创建新结点作为根结点
    if ((*T) == NULL)
    {
        // 性质二：根结点为黑色
        (*T) = NewNode(0, x);
        return;
    }

    // 根据二叉排序树的性质查找插入位置
    RBNode *node = (*T), *parent;
    while (node)
    {   
        parent = node;
        if (node->data > x)
        {
            node = node->lchild;
        }
        else if (node->data < x)
        {
            node = node->rchild;
        }
        else
        {
            printf("插入失败，存在相同数据\n");
            return;
        }      
    }
    // 根据查找到的位置的父结点插入
    node = NewNode(1, x);
    if (parent->data > x)
    {
        parent->lchild = node;
    }
    else
    {
        parent->rchild = node;
    }
    node->parent = parent;
    
    
    // 若父结点为红色，则不符合性质三：红色结点的孩子结点均为黑色
    if (parent->color == 1)
    {
        // printf("父结点(%c)为红色，需要进行调整!\n", parent->data);
        RBTreeAdjust(node);
    }
}



// 先序遍历
void PreOrderTraverse(RBTree T)
{
    if (T)
    {
        printf("%c", T->data);
        T->color == 0 ? printf("[黑] ") : printf("[红] ");
        PreOrderTraverse(T->lchild);
        PreOrderTraverse(T->rchild);
    }
}


int main()
{
    RBTree T;
    DataType x;
    InitRBTree(&T);

    while (1)
    {
        fflush(stdin);
        printf("输入插入数据:");    // 测试数据：FEKDCABNMOP
        scanf("%c", &x);
        if (x == '#')
        {
            break;
        }
        RBTreeInsert(&T, x);
        printf("先序遍历:");
        PreOrderTraverse(T);
        printf("\n\n");
    }
    system("pause");
    return 0;
}

3. 测试结果

在这里插入图片描述
在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/139531.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

JavaScript---DOM---节点操作---12.3

JavaScript---DOM---节点操作---12.3

为什么学节点操作&#xff1f; 获取元素通常使用两种方式&#xff1a; 1.利用DOM提供的方法获取元素 document.getElementByld()document.getElementsByTagName()document.querySelector等逻辑性不强&#xff0c;繁琐 2.利用节点层级关系获取元素&#xff08;操作更简单&…
阅读更多...
标准模板库STL

标准模板库STL

一、概述 1.1 STL的概念和作用 STL的概念&#xff1a;全称为 Standard Template Library STL的作用&#xff1a; 首先STL并不是语言的一部分&#xff08;一开始并没有&#xff09;它就是一个工具库, 没有这个工具时程序员写程序都要自己做&#xff08;例如&#xff1a;数据结…
阅读更多...
软件生命周期阶段有几个？常见软件生命周期模型有哪些？

软件生命周期阶段有几个？常见软件生命周期模型有哪些？

软件生命周期阶段及常见的软件生命周期模型&#xff0c;软件生命周期是指一个计算机软件从功能确定、设计&#xff0c;到开发 成功投入使用&#xff0c;并在使用中不断地修改、增补和完善&#xff0c;直到停止该软件的使用的全过程。 　生命周期从收到应用软件开始算起&#x…
阅读更多...
springboot 多模块项目构建【创建√ + 启动√ 】

springboot 多模块项目构建【创建√ + 启动√ 】

一、多模块项目构建 1. 先建立父级目录demo-parent 2. 把父级目录src删除&#xff0c;再建立子级模块 3. 建立子级模块model,dao,service,common.utils等相同步骤 4. 建立启动模块boot, 创建Spring Boot 启动类 package com.example;import org.springframework.boot.SpringAp…
阅读更多...
http服务转https服务（Nginx 服务器 SSL 证书安装部署）

http服务转https服务（Nginx 服务器 SSL 证书安装部署）

安装的服务一直使用的是http&#xff0c;结果有客户要求必需使用https,下面是整理的步骤1、证书下载&#xff1a;&#xff08;要用域名申请的账号登录&#xff09;域名所在服务商一般都可以下载免费证书&#xff0c;我们用的域名是腾讯云的&#xff0c;所以在腾讯云上申请了免费…
阅读更多...
高通开发系列 - gpio模拟输出PWM或者CLK时钟

高通开发系列 - gpio模拟输出PWM或者CLK时钟

By: fulinux E-mail: fulinux@sina.com Blog: https://blog.csdn.net/fulinus 喜欢的盆友欢迎点赞和订阅！ 你的喜欢就是我写作的动力！ 目录 问题背景平台信息GPIO输出CLKdts添加节点修改内核gcc时钟配置驱动文件编译运行gpio模拟PWM输出CLKdts中的配置GPIO模拟PWM驱动文件编译…
阅读更多...
MSF信息收集

MSF信息收集

Nmap扫描 db_nmap -sV 192.168.1.0/24Auxiliary 扫描模块 ● RHOSTS表示 192.168.1.20-192.168.1.30 、 192.168.1.0/24,192.168.11.0/24&#xff08;扫描两个网段&#xff09; file:/root/host.txt (将需要扫描的主机访问文本中)● search arp use auxiliary/scanner/d…
阅读更多...
网站收录查询方法，网站收录减少的原因

网站收录查询方法，网站收录减少的原因

网站收录就是与互联网用户共享网址&#xff0c;网站收录前提是网站首页提交给搜索引擎&#xff0c;蜘蛛才会光顾&#xff0c;每次抓取网页时都会向索引中添加并更新新的网站&#xff0c;站长只需提供顶层网页即可&#xff0c;不必提交各个单独的网页。抓取工具能够找到其他网页…
阅读更多...
华为matebook X 笔记本没开什么程序，有时经常慢卡

华为matebook X 笔记本没开什么程序，有时经常慢卡

环境&#xff1a; 华为matebook X CPU &#xff1a;英特尔4核8线程10代 i5 内存&#xff1a;海力士16G 固态硬盘500G 问题描述&#xff1a; 华为matebook X 没开什么程序&#xff0c;经常慢卡&#xff0c;平时就是打开钉钉&#xff0c;处理处理文档&#xff0c;之前优化过…
阅读更多...
模板题---1.5（单调栈，单调队列，kmp,manachar）

模板题---1.5（单调栈，单调队列，kmp,manachar）

这里写目录标题1.单调栈2.单调队列3.kmp算法4.manachar算法这里记录几个基本的数据结构算法1.单调栈 要点&#xff1a; 数据结构是栈栈要维护单调性 这就是单调栈的基本定义 举个例子: &#xff08;栈底&#xff09;1 3 5 7 &#xff08;栈顶&#xff09; <-------这就是…
阅读更多...
行为型模式 - 备忘录模式Memento

行为型模式 - 备忘录模式Memento

学习而来&#xff0c;代码是自己敲的。也有些自己的理解在里边&#xff0c;有问题希望大家指出。 模式的定义与特点 在备忘录模式&#xff08;Memento Pattern&#xff09;下&#xff0c;为的是在不破坏封装性的前提下&#xff0c;捕获一个对象的内部状态&#xff0c;并在该对象…
阅读更多...
【C++ Primer】阅读笔记（2）：const | constexpr | 类型别名 ｜auto

【C++ Primer】阅读笔记（2）：const | constexpr | 类型别名 ｜auto

目录 简介const指针顶层const与底层const常量表达式constexpr类型别名auto参考结语简介 Hello！ 非常感谢您阅读海轰的文章，倘若文中有错误的地方，欢迎您指出～ ଘ(੭ˊᵕˋ)੭ 昵称：海轰 标签：程序猿｜C++选手｜学生 简介：因C语言结识编程，随后转入计算机专业，获得过…
阅读更多...
CTF中的PHP特性函数（下）

CTF中的PHP特性函数（下）

前言 上篇文章讲的进阶一些的PHP特性不知道大家吸收的怎么样了&#xff0c;今天作为本PHP特性函数的最后一篇&#xff0c;我也会重点介绍一些有趣的PHP特性以及利用方法&#xff0c;下面开始我们今天的内容分享。 parse_str parse_str()这个函数会把查询字符串解析到变量中。…
阅读更多...
二叉树——链式存储

二叉树——链式存储

✅<1>主页&#xff1a;我的代码爱吃辣 &#x1f4c3;<2>知识讲解&#xff1a;数据结构——二叉树 &#x1f525;<3>创作者&#xff1a;我的代码爱吃辣 ☂️<4>开发环境&#xff1a;Visual Studio 2022 &#x1f4ac;<5>前言&#xff1a;上期讲了…
阅读更多...
LinkedList与链表（一）（非循环单向链表）

LinkedList与链表（一）（非循环单向链表）

ArrayList的缺陷通过ArrayList上节课的学习&#xff0c;我们了解到如果ArrayList要删除或插入一个元素&#xff0c;后面的元素都要进行移动&#xff0c;时间复杂度为O(n),效率比较低&#xff0c;因此ArrayList不适合做任意位置的插入和删除操作比较多的场景。因此java集合又引入…
阅读更多...
Python if __name__ == “__main__“ 用法

Python if __name__ == “__main__“ 用法

文章目录1 前言2 原理3 __name__变量的作用参考1 前言 在很多Python程序中&#xff0c;我们都会遇到if __name__ "__main__"的情况&#xff0c;却不知道为何要这样做 在很多编程语言中&#xff0c;如C、Java等&#xff0c;都需要程序的入口&#xff0c;一般都是ma…
阅读更多...
MySql锁机制（全网最全、最详细、最清晰）

MySql锁机制（全网最全、最详细、最清晰）

1、MySql锁机制 锁机制的作用&#xff1a; 解决因为资源共享&#xff0c;而造成的并发问题。 没有锁机制时&#xff1a; 例如一号用户和二号用户都要去买同一件商品&#xff08;假如这件商品是一件衣服&#xff09;&#xff0c;一号用户手速稍微快了一些&#xff0c;于是就…
阅读更多...
从事软件测试需要学自动化么

从事软件测试需要学自动化么

相信许多对软件测试有过一点了解的人&#xff0c;对自动化都不会感到陌生。我们常常会听到一定软件测试人员一定要学自动化的说法&#xff0c;那么很多人都会有这样的疑问&#xff0c;从事软件测试为什么要学自动化&#xff1f;事实上&#xff0c;如今只会功能测试的从业者往往…
阅读更多...
光波导成为AR眼镜迭代新趋势，二维扩瞳几何光波导潜力彰显

光波导成为AR眼镜迭代新趋势，二维扩瞳几何光波导潜力彰显

关注AR眼镜的朋友可能都会发现&#xff0c;近期新品迭代的一个趋势是持续在小型化、轻量化方向演进。与一年前光学方案主要以BirdBath不同的是&#xff0c;消费级AR眼镜正快速向光波导方案探索和转变。这一点在最近发布的众多新品AR眼镜中就能明显的感受到&#xff0c;以视享G5…
阅读更多...
堆排序 TopK 优先级队列的部分源码 JAVA对象的比较

堆排序 TopK 优先级队列的部分源码 JAVA对象的比较

一.堆排序:我们该如何借助堆来对数组的内容来进行排序呢&#xff1f; 假设我们现在有一个数组&#xff0c;要求从小到大进行排序&#xff0c;我们是需要进行建立一个大堆还是建立一个小堆呢&#xff1f; 1)我的第一步的思路就是建立一个小堆&#xff0c;因为每一次堆顶上面的元…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023