这里写目录标题
- 1.单调栈
- 2.单调队列
- 3.kmp算法
- 4.manachar算法
这里记录几个基本的数据结构算法
1.单调栈
要点:
- 数据结构是栈
- 栈要维护单调性
这就是单调栈的基本定义
举个例子:
(栈底)1 3 5 7 (栈顶)
<-------这就是一个单调栈😋
当然,定义很简单,但是用的时候不一定很顺利,相反,用的时候非常的绕圈子,但是首先定个基调,这个算法非常简单。
拿几个题目作为模板题来练习:
acwing单调栈
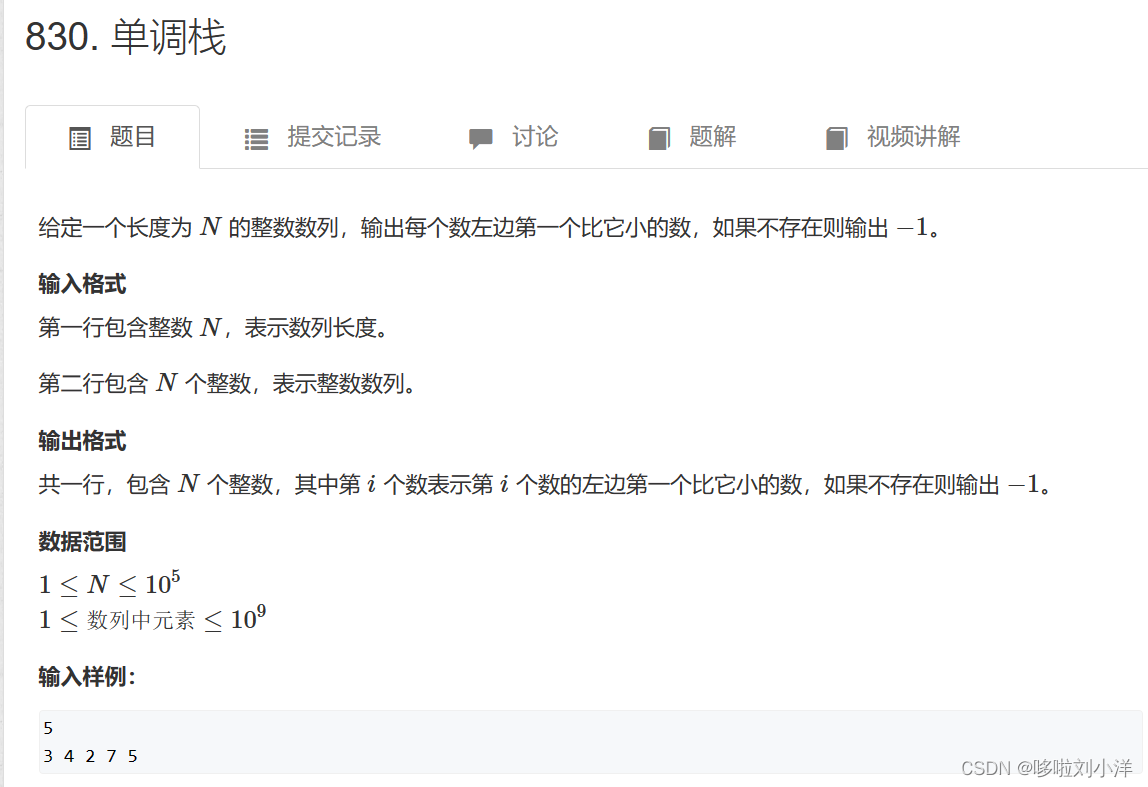

这道题是单调栈最简单的题。
目的是:找到左边第一个小于当前的数。
那么这种情况是满足的:数组从左到右严格递增。
这样就可以保证每个数左边第一个小于自己的数被快速找到,因为答案就是左边第一个数。
比如:
1 2 3 4 5
1,2,3,4,5左边第一个小于自己的数就是他们本身左边第一个数。
最后,目的就是去构建并且维护这样一个单调的数组。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<stack>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int b[N];
stack<int>st;
int n;
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++)
{
while (!st.empty() && st.top() >= a[i]) //如果栈不空,且栈顶元素大于等于当前元素,将栈顶弹出(维护栈单调性)
st.pop();
if (st.empty()) //如果栈空,说明a[i]左边没有比它小的元素
b[i] = -1;
else //否则有,记录
b[i] = st.top();
st.push(a[i]);
}
for (int i = 1; i <= n; i++)
cout << b[i] << " ";
return 0;
}
也可以不需要数组b,用一些小技巧:
-----00
#include<iostream>
#include<cstring>
#include<algorithm>
#include<stack>
using namespace std;
const int N = 1e5 + 10;
int a[N];
stack<int>st;
int n;
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= n; i++)
{
while (!st.empty() && st.top() >= a[i]) //如果栈不空,且栈顶元素大于等于当前元素,将栈顶弹出(维护栈单调性)
st.pop();
int t=a[i];
if(st.empty())
a[i]=-1;
else
a[i]=st.top();
st.push(t);
}
for (int i = 1; i <= n; i++)
cout << a[i] << " ";
return 0;
}
继续练习,这个题掌握了,单调栈基本上就一知半解了😋
洛谷里面有几个题:
1.P1901 发射站
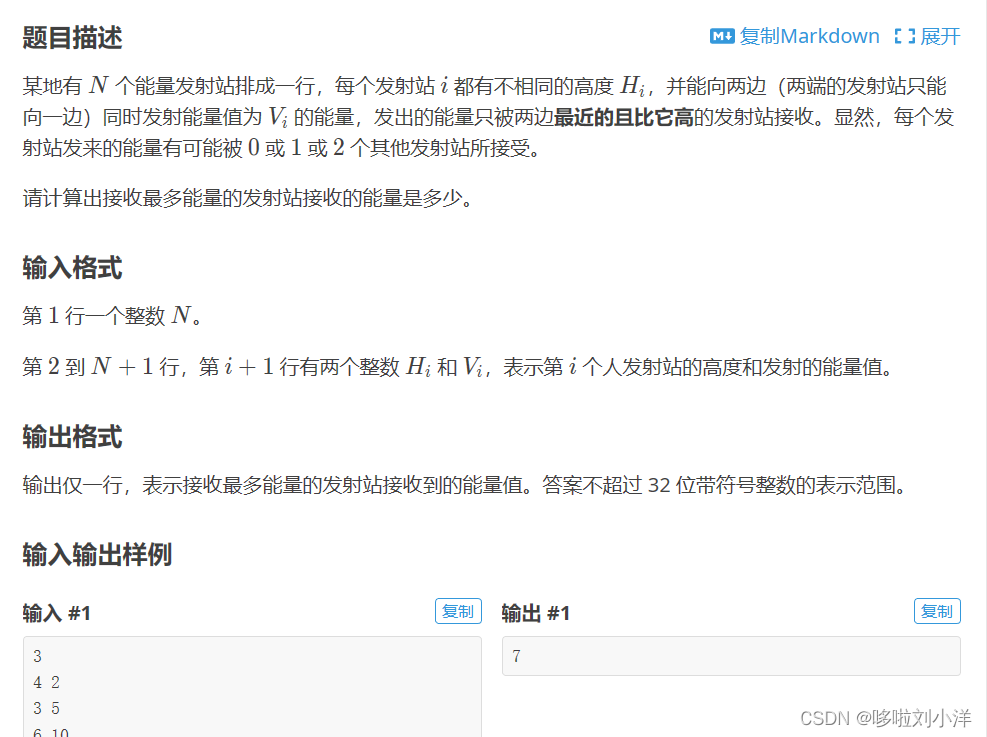
这个题目翻译一下:
分别找到比第i个数左边第一个比第i个数高的数和右边第一个高的数。
那么分为两个问题
1.找到第i个数左边第一个比它高的数
2.找到第i个数右边第一个比它高的数
那么这样的序列可以一次找到左边第一个比它高的数:
5 4 3 2 1
那么这样的序列可以一次找到右边第一个比他高的数:
1 2 3 4 5
如果这样来拆分,实际上就是套用了两次模板。
#include<iostream>
#include<cstring>
#include<algorithm>
#include<stack>
using namespace std;
const int N = 1e6 + 10;
struct node
{
int h, v,i;
}A[N];
int energy[N][2];//energy[i][0]表示左边第一个比i高的位置下标,energy[i][1]表示右边第一个比i高的下标
int ans[N];
stack<node>st;
int n;
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
int a, b;
cin >> a >> b;
A[i].h = a, A[i].v = b, A[i].i = i;
}
//分别找出比当前数左边第一个高的和右边第一个高的
//左边第一个高
for (int i = 1; i <= n; i++) //只要维护的是一个单调递减数列,那么就是合理的
{
while (!st.empty() && st.top().h<= A[i].h)st.pop(); //如果当前能量塔高度大于等于栈顶,栈顶元素弹出
if (st.empty())
energy[i][0] = 0;
else
energy[i][0] = st.top().i;
st.push(A[i]);
}
//先清空栈重复利用
while(!st.empty())
st.pop();
//右边第一个高,实际上就是反过来找左边第一高,
for (int i = n; i >= 1; i--)
{
while (!st.empty() && st.top().h <= A[i].h)st.pop(); //如果当前能量塔高度大于等于栈顶,栈顶元素弹出
if (st.empty())
energy[i][1] = 0;
else
energy[i][1] = st.top().i;
st.push(A[i]);
}
int Max = -99999;
for (int i = 1; i <= n; i++) //由于每个能量塔都会传播能量到左右,所以用一个数组ans记录所有接收的能量
{
ans[energy[i][0]] += A[i].v;
ans[energy[i][1]] += A[i].v;
}
for (int i = 1; i <= n; i++) //最后找到接受能量最多的
Max = max(Max, ans[i]);
cout << Max << endl;
return 0;
}
2.单调队列
和单调栈大同小异,维护队列的单调性
滑动窗口
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e6+10;
int a[N]; ///模拟数组
int q[N];
int tt,hh;
int n,k;
int main()
{
cin>>n>>k;
for(int i=0;i<n;i++)
cin>>a[i];
hh=0,tt=-1; //hh是队头(左),tt是队尾(右)
for(int i=0;i<n;i++) //维护单调递增队列
{
if(hh<=tt&&q[hh]<i-k+1)hh++; //如果窗口左边下标大于队头下标,那么队头弹出,hh右移一个单位
while(hh<=tt&&a[q[tt]]>=a[i])tt--; //维护单调递增队列
q[++tt]=i;
if(i>=k-1)
cout<<a[q[hh]]<<" ";
}
cout<<endl;
hh=0,tt=-1; //hh是队头(左),tt是队尾(右)
for(int i=0;i<n;i++) //维护单调递增队列
{
if(hh<=tt&&q[hh]<i-k+1)hh++; //如果窗口左边下标大于队头下标,那么队头弹出,hh右移一个单位
while(hh<=tt&&a[q[tt]]<=a[i])tt--; //维护单调递增队列
q[++tt]=i;
if(i>=k-1)
cout<<a[q[hh]]<<" ";
}
cout<<endl;
return 0;
}
3.kmp算法
首先定一个基调,这是一个异常烦人的算法,和那个manachar算法一样折磨人。
这题注意,字符下标要从1开始,否则ne[j]会出现j==-1的清空,数组不允许下标是-1
题目:KMP模板
学习链接,任何人都可以看懂:董晓老师算法
#include<iostream>
using namespace std;
const int N=1e6+10;
char S[N],P[N];
int ne[N];
int n,m;
int main()
{
cin>>n;
scanf("%s",P+1);
cin>>m;
scanf("%s",S+1);
for(int i=2,j=0;i<=n;i++)
{
while(j&&P[i]!=P[j+1])j=ne[j];
if(P[i]==P[j+1])j++;
ne[i]=j;
}
for(int i=1,j=0;i<=m;i++)
{
while(j&&S[i]!=P[j+1])j=ne[j];
if(S[i]==P[j+1])j++;
if(j==n)
{
cout<<i-n<<" ";
j=ne[j];
}
}
return 0;
}
4.manachar算法
这个问题的来源是解决这样一个问题:给定一个字符串S,找出这个字符串里面的最长回文子串。
比如abbaba ,其中最长的回文子串是abba,所谓回文串,就是正着反着读是一样的。而子串一定要保证连续的。
题目:最长回文子串
这个题和kmp扩展算法基本一样。
class Solution {
public:
string longestPalindrome(string s)
{
//第一步构造新字符串
string ss="";
ss+="@#";
for(int i=0;i<s.length();i++)
{
ss+=s[i];
ss+="#";
}
//构造一个数组d[N]记录所有字符的回文半径
//初始化1,d[i]=1表示以i为中心的字符串的回文半径为1
vector<int>d(ss.length(),1);
//开始manachar算法
for(int i=1,boxl=0,boxr=0,x=0;i<ss.length();i++)
{
int y=2*x-i; //y是元素ss[i]关于x的对称点
if(boxr>=i)d[i]=min(d[y],boxr-i+1);
while(ss[i+d[i]]==ss[i-d[i]])d[i]++;
if(boxr<i+d[i]-1) //当前盒子的右端点大于老盒子的右端点
{
x=i;
boxl=i-d[i]+1;
boxr=i+d[i]-1;
}
}
int a,b; //记录最长回文串的下标和回文半径
for(int i=1;i<ss.length();i++)
{
if(d[i]>a)
{
a=d[i];
b=i;
}
}
string ans="";
for(int i=b-a+1;i<=b+a-1;i++)
{
if(ss[i]!='#')
ans+=ss[i];
}
return ans;
}
};
不用leetcode的话这样写
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1e7 + 10;
int d[N];
string s, ss,ans;
string manachar(string &s)
{
ss = ans = "";
ss += "$#";
for (int i = 0; i < s.length(); i++)
{
ss += s[i];
ss += "#";
}
for (int i = 0; i < ss.length(); i++)
d[i] = 1;
for (int i = 1, l = 0, r = 0, x = 0; i < ss.length(); i++)
{
int y = 2 * x - i;
if (r >= i)d[i] = min(d[y], r - i + 1);
while (ss[i + d[i]] == ss[i - d[i]])d[i]++;
if (r < i + d[i] - 1)
{
x = i;
l = i - d[i] + 1;
r = i + d[i] - 1;
}
}
int index=0, Maxlen=-1;
for (int i = 1; i < ss.length(); i++)
{
if (Maxlen < d[i])
{
Maxlen = d[i];
index = i;
}
}
for (int i = index - Maxlen + 1; i <= index + Maxlen - 1; i++)
{
if (ss[i] != '#')
ans += ss[i];
}
puts(" ");
return ans;
}
int main()
{
cout << "输入字符串:";
cin >> s;
cout << "最长回文子串是:" << endl;
cout << manachar(s) << endl;
return 0;
}





![[Vue的数据绑定]一.Vue的数据绑定;二.Vue的事件绑定;三.Class和Style的绑定;四.Vue的过滤器;五.Vue脚手架的使用](https://img-blog.csdnimg.cn/img_convert/08076e28d78c39db246c534ffc74faed.png)