2018年认证杯SPSSPRO杯数学建模

基于轮廓特征的机械零件位置识别研究

C题 机械零件加工过程中的位置识别

原题再现：

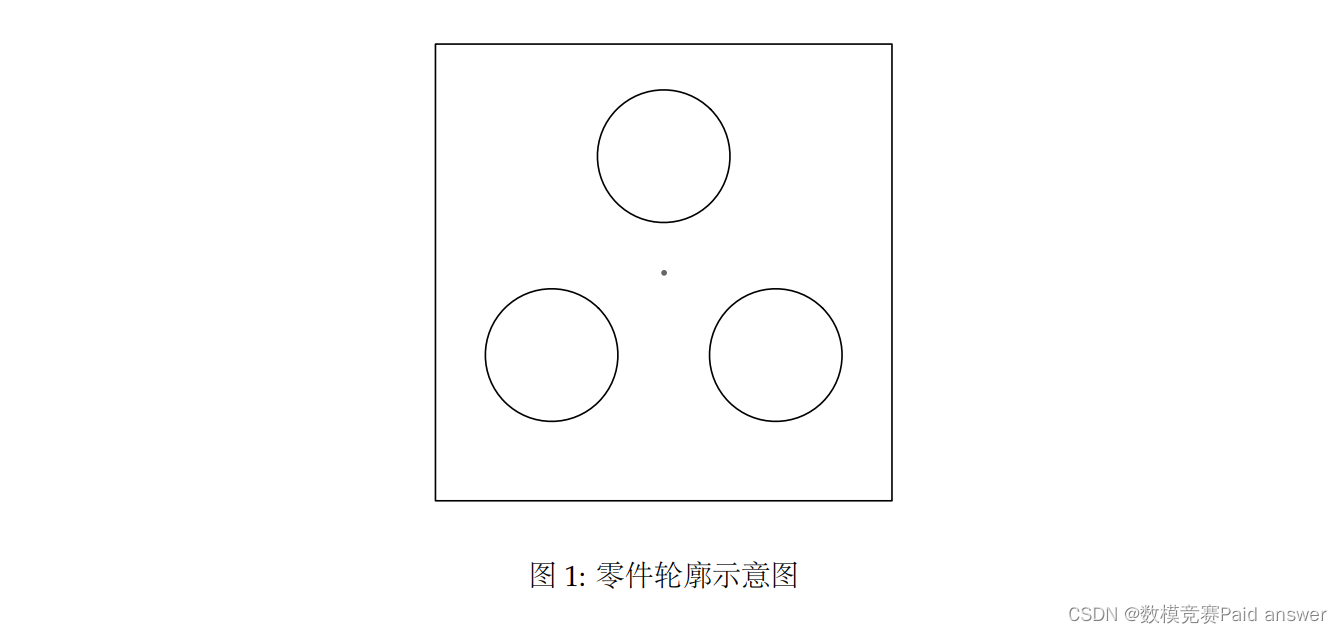
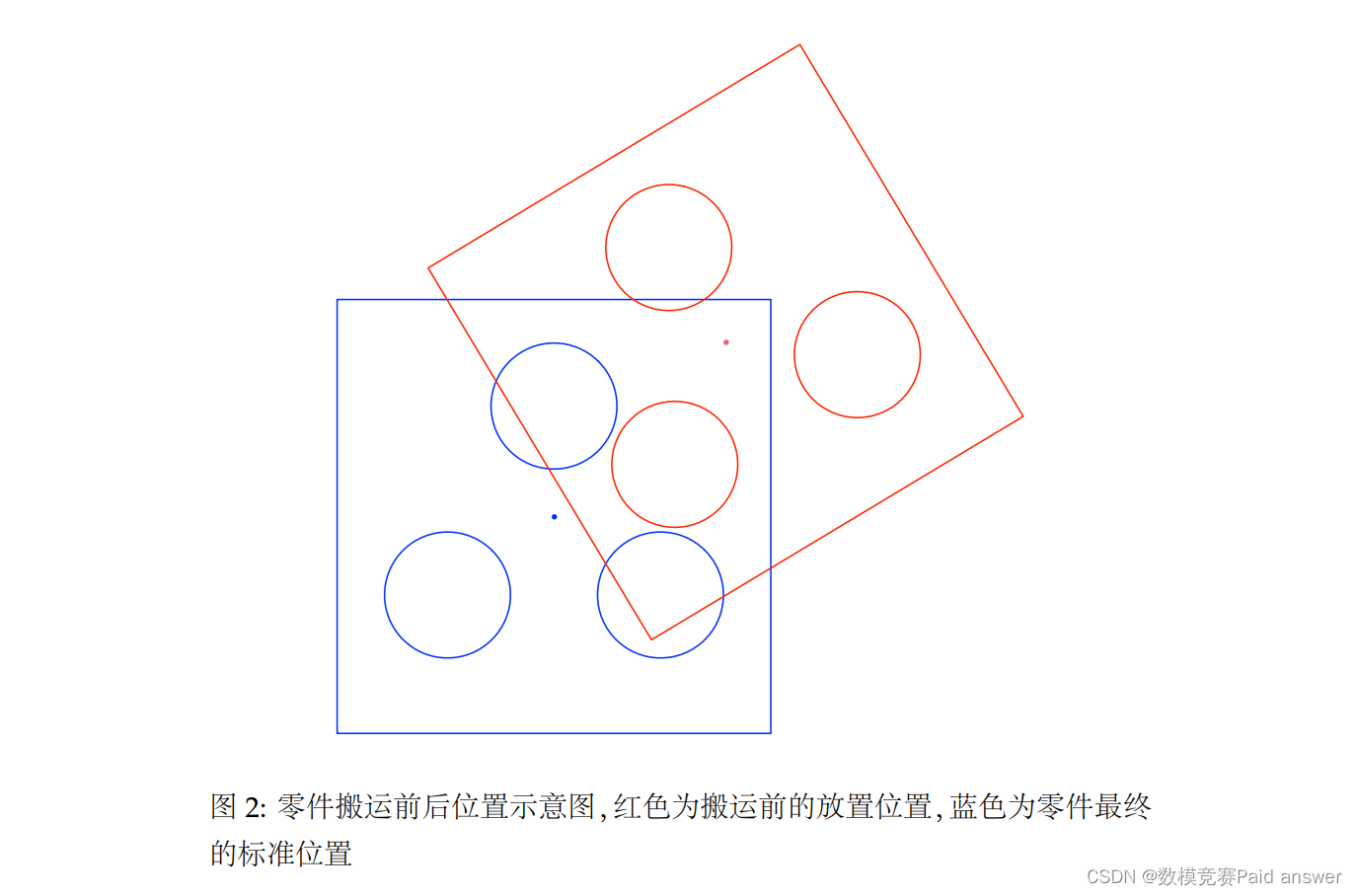
  在工业制造自动生产线中，在装夹、包装等工序中需要根据图像处理利用计算机自动智能识别零件位置，并由机械手将零件自动搬运到特定位置。某零件轮廓如图 1 所示，图2 表示零件搬运前后的位置示意图。
  第一阶段问题：
  1. 根据附件 DATA1 中给出的零件轮廓数据，请建立数学模型，识别计算出给定零件的位置坐标，并分析评价求解零件位置的算法是否快速高效。
  2. 问题 1 讨论的是单个零件放置于平面操作台上的情况。有时我们需要处理多个零件显示在同一图像中的情况，请根据附件 DATA2 中的数据，建立数学模型，识别出不同零件的位置。

整体求解过程概述(摘要)

  图像位置识别（机器视觉）在工业生产中应用广泛。本文首先通过霍夫变换提取给定零件轮廓中发直线和圆特征，进而利用峰值检测和 K-means 聚类分析方法准确识别有效的直线和圆特征；依次建立零件轮廓的绝对坐标系和零件标准位置模板坐标系；分别采用基于零件全特征（随机抽样）和基于零件主要特征的方式提取零件轮廓的有效像素点，并通过模拟退火算法求解了不同迭代次数下采用这两种方式识别零件位置的速度（时间）和精度。采用目标轮廓分割法提取零件的二维轮廓像素矩阵，之后通过模拟退火算法求解多个零件轮廓的位置和识别速度（时间）。
  问题 1：对于被测零件几何特征未知的情况，以 DATA1 中的初始图像像素起始点为原点，沿行增加与列增加的方向建立绝对直角坐标系，得到了零件轮廓中矩形的四个顶点坐标，即（182, 172）、（266, 317）、（334, 84）和（414, 230），三个圆的圆心坐标为（247, 288）、（188, 253）、（183, 329），且半径均为 26，最低识别精度为 99.1%。对于几何特征已知情况，在初始图像中某一确定位置处建立零件的标准位置模板，分别随机提取标准位置模板的有效像素点和被测零件的有效像素点，以被测零件轮廓图像的有效像素抽样点与标准位置模板的有效像素抽样点的最短距离和最小为目标，以平移量和旋转角度为自变量，通过模拟退火算法(迭代5000次)得到被测零件相对中心位置为(296.0209,200.6858)，逆时针旋转 28.0433°，识别时间为 2.306s，最低识别精度为 95%。
  问题 2：将多个零件的识别分成零件分割和零件定位两步。在 DATA2 的初始图像中建立直角坐标系，采用问题 1 的方法获得被测零件轮廓组的 6 个圆心坐标，并对其进行聚合分类；以几何中心为圆心，以矩形轮廓对角线为直径做圆，划分成 2 个独立领域；并提取独立领域内的二维图像信息，采用问题 1 方法，求解得到零件 a 和零件 b 中心相对于标准位置模板中心的位置分别为（239.9272, 400.0000）和（305.9829, 199.5862），对应的逆时针旋转角度为 60.64°和 29.31°。
  模型改进：为提高识别速度，建立基于零件几何特征（3 个圆心）的快速识别模型，即将目标函数简化为被测零件的圆心与标准位置模板圆心的最短距离和最小，通过模拟退火算法（迭代为 5000 次）进行求解。零件 a 的识别时间为 0.312s，最低识别精度为98.8%，零件 b 的识别时间为 0.292s，最低识别精度为 97.6%。

问题分析：

  问题 1 的分析
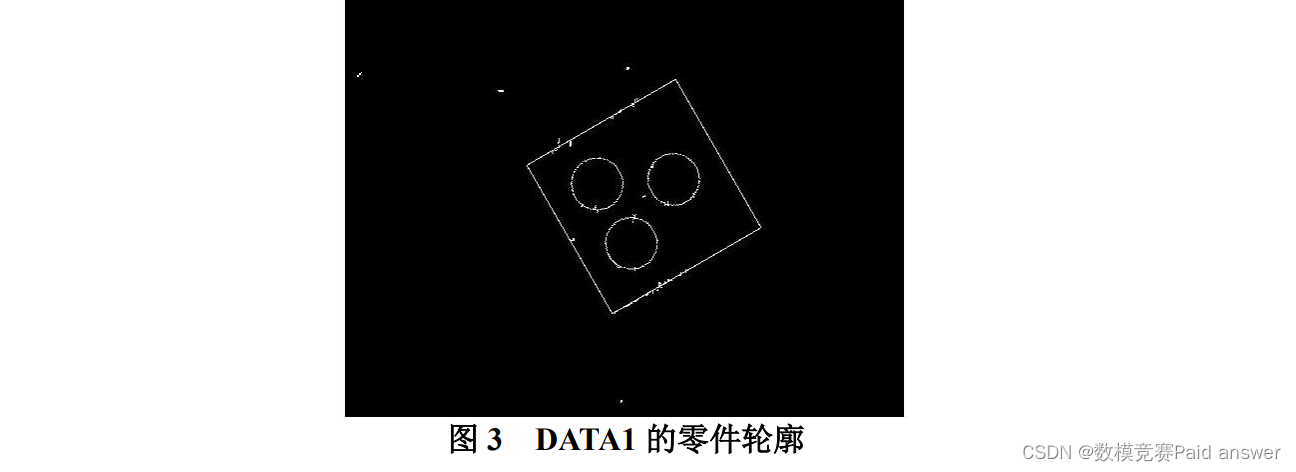
  本问题要求根据附件 DATA1 中给出的零件轮廓数据，识别并计算出给定零件的位置坐标，DATA1 的零件轮廓如图 3 所示。零件的识别分类主要包括特征提取和识别。颜色特征、纹理特征、形状特征、和几何特征是图像的四大特征[1]。从图 1 可以看出本问题给出的图是机械零件的二维轮廓图，可知该零件具有不可形变的特点，并且为白色（颜色特征不明显），为此本文考虑采用几何、形状特征对其进行识别。常见的几何特征为轮廓个数、面积、周长，而形状特征一般有点、直线、圆、椭圆等。根据本题给出的零件轮廓图，可以很容易地看出其主要包括 3 个圆、4 条直线且两两垂直（或矩形）。为此问题 1 中的轮廓识别就变成了圆的识别和直线（或矩形）的识别问题。霍夫变换[2]（Hough Transform）是由图像空间的边缘点去计算参数空间中参考点的可能轨迹，从而在计算机的累加器中给计算出的参考点计数，最后选出峰值。因为它将直角坐标系中的线变为极坐标中的点，故一般常将霍夫变换称为线、点变换。根据这个原理，可以用霍夫变换提取直线、圆等常规的几何特征。为此问题 1 可以利用霍夫变换识别已知零件轮廓的圆特征和直线特征（矩形）。

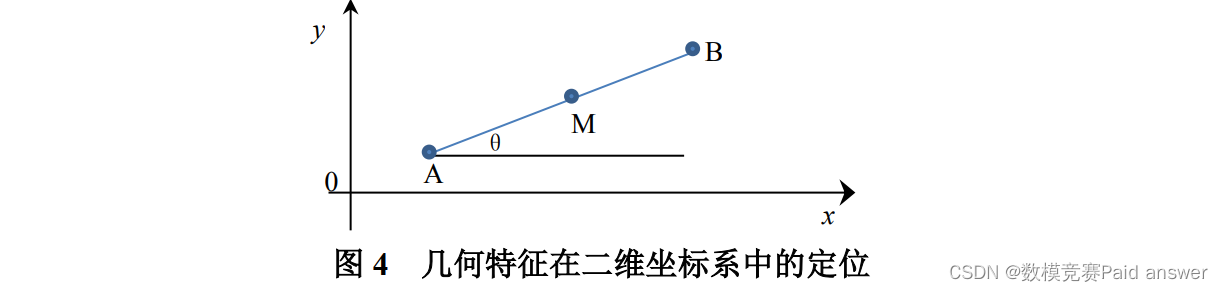
  判断某一图像的位置通常需要定义参考坐标系或者参考物，之后根据参考坐标系或参考物来判断图形的相对位置。而零件的位置信息又可分为零件的绝对位置（与参考坐标系或者参考物相比）及零件本身几何特征之间的相对位置（如本题中的圆、直线之间的相对位置）。在二维坐标系中（假如已知参考坐标系），判断某一个点通常只需知道其横向坐标（x 向）和纵向坐标（y 向），而定位线段不仅需要知道该线段特征（如中心、起点或终点）的坐标，还需知道其相对于横轴（x 向）或纵轴（y 向）的角度，具体可见图 4 所示。

  为此，要想准确定位问题 1 给出的零件轮廓图，即确定其位置坐标，可以通过相应的几何特征进行平移及旋转（即通过平移和旋转后使其恢复到参考物状态）。可以推知，问题 1 可具体化为零件轮廓（可取其几何中心点）的坐标平移与轮廓自身旋转的问题。通过上述分析可知，位置的定位可以通过图像的旋转和平移来实现[3]。就问题 1 而言，可在初始图像（DATA1 中的零件轮廓图）中建立直角坐标系，通过霍夫变换来检测轮廓中的几何特征（直线与圆），之后结合 K-means 聚类分析确定零件轮廓中准确的三个圆和四条直线（矩形）的信息，即三个圆的半径及方程、直线长度，为此，零件的位置信息也可相应地计算得到[4-7]。
  考虑到问题 1 中零件轮廓的几何特征和形状特征信息，如矩形轮廓边长、圆的半径及圆心相对位置均可通过 Matlab 简单计算得到（假设长度单位为 1），因而可在某一确定的位置处建立零件的标准模板，见图 5。从 DATA1 中的零件轮廓和零件的标准模板轮廓中随机取部分像素点坐标，依次计算 DATA1 提取的每一像素点坐标到标准模板轮廓所提取的像素点坐标的最小距离，即以求解距离和最小为目标，以给定零件轮廓的平移至标准模板位置的移动量和旋转角度为设计变量，建立数学模型，并通过优化算法（可选用模拟退火方法）求解该模型，即可求得的移动量与旋转角度，从而反求零件的位置与角度（相对于标准模板）。该方法可称为模板匹配法。

  问题 2 的分析
  本问题要求根据附件 DATA2 中给出的多个零件轮廓，识别一幅图像中多个零件的不同位置信息。利用 Matlab 可将 DATA2 中的数据进行图像再现，如图 6 所示。从图 6可以看出，图中包含 2 个相同的零件轮廓（每个轮廓与 DATA1 中的轮廓相同，仅姿态不同），即总共包含 6 个圆和 8 条直线。如采用问题 1 的方法直接对图 6 中的 2 个零件轮廓进行位置求解则会发生轮廓特征重复的问题，即无法获取所需轮廓的难题。为此，解决问题 2 的关键在于分割 2 个零件轮廓，即使 2 个零件轮廓独立显示在图像中。分割完 2 个轮廓后，分别采取问题 1 的办法即可实现 2 个零件轮廓的位置定位。

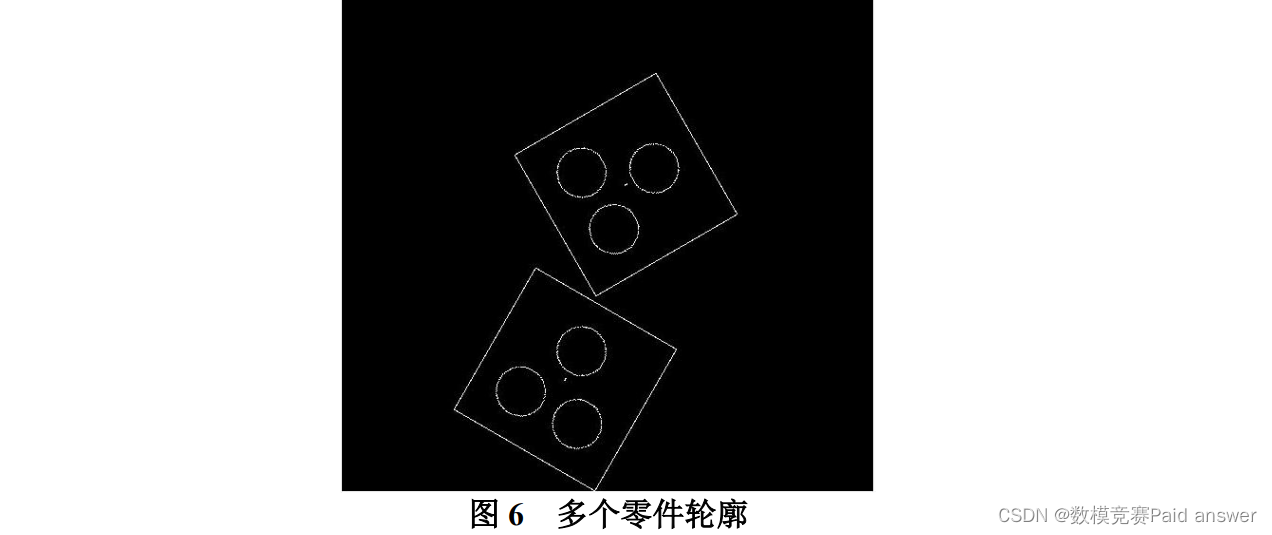
  从图像中分离并提取目标（也称轮廓分割）可以看作是基元轮廓检测的一种推广。通常有基于目标轮廓和基于目标区域两种方法用于轮廓分割。目标轮廓分割法：考虑目标与图像中其他部分的界限，如果能确定目标轮廓界限，就可将目标与图像的其他部分割开。在这种方法中，除了检测出轮廓点将其连接起来，还可以边检测轮廓点边的连接。而基于目标区域法是考虑所有属于目标区域的像素，如果能确定出每个属于目标的像素就可以获得完整的目标。通常是假设构成目标区域的像素的灰度值大于某个特定的阈值，确定这个阈值把目标区分开。考虑到问题 2 中的 2 个零件轮廓为简单的圆和直线轮廓，为了提高识别速度，本文采用目标轮廓分割法[8]将 2 个零件轮廓分割开。
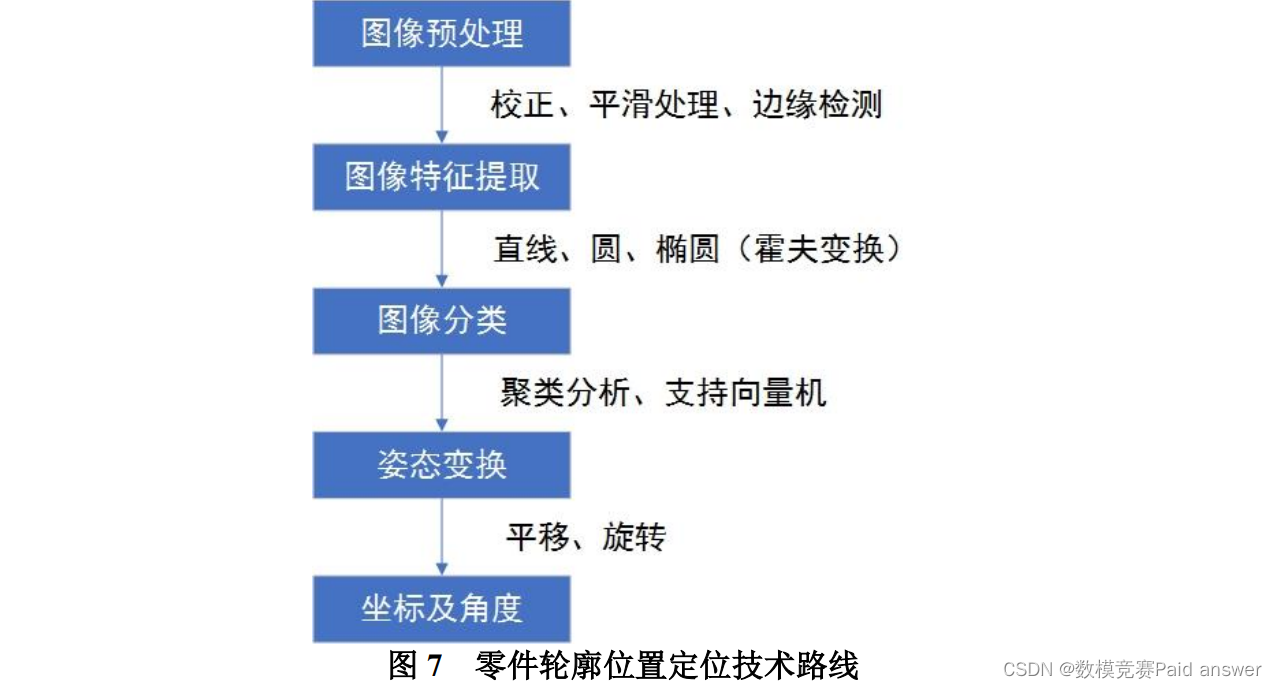
  为此问题 2 中轮廓分割的具体方案为：在初始图像中建立直角坐标系，通过霍夫变换进行几何特征圆的检测，结合 K-means 聚类分析方法，获取 DATA2 中 6 个圆心的坐标，随后对所得的 6 圆心坐标再次进行 K-means 聚类分析，从而可得到每个零件轮廓的近似中心点坐标，以近似中心点坐标为中心，零件模板矩形的对角线一半为半径，通过Matlab 画一轮廓，即可将该区域数据的零件信息分割出来。针对于分割出来的零件轮廓的位置坐标及旋转角度的确定，依然可采用问题 1 的方法对其进行以求解。即求解每个给定零件与标准位置模板部分位置坐标的和最小为目标函数，建立数学模型的方法，根据平移的移动量与旋转的角度，对其反求即可得到图像中 2 个零件轮廓的位置坐标和角度。综上，零件轮廓位置定位的技术路线如图 7 所示。

  考虑到本问题 1 和 2 中的噪点对零件轮廓位置的定位没有影响，因此，本文在进行零件轮廓定位之前并未进行图像预处理。

模型假设：

  （1）零件轮廓为二维轮廓。
  （2）多个零件在一副图像中不会发生重叠现象。
  （3）图像位置的偏差在机械零件加工中处于合理误差范围（即机器手或者夹具是可以准确定位和夹紧，比如采用锥形定位或半销定位）。
  （4）图像中的噪声（非圆及非矩形上的点不会影响位置的定位，因此不必进行滤波或图像平滑处理）。

论文缩略图：

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

clc
clear
load('DATA1.mat')
BW=D1;
thresh=[0.01,0.17]; 
sigma=2; %定义高斯参数 
f = edge(double(BW),'canny',thresh,sigma); 
figure(1),imshow(f,[]); 
title('canny 边缘检测'); 
[H, theta, rho]= hough(f,'RhoResolution', 0.5); 
rho=rho;
peak=houghpeaks(H,4); 
hold on 
lines=houghlines(f,theta,rho,peak); 
figure,imshow(f,[]),title('Hough Transform Detect Result'),hold on 
for k=1:length(lines) 
 xy=[lines(k).point1;lines(k).point2]; 
 plot(xy(:,1),xy(:,2),'LineWidth',4,'Color',[.6 .6 .6]); 
end

%%首先导入像素矩阵 D1,再设置如下参数
clc,clear
load('DATA1.mat')
step_r = 1;
step_angle = 0.1;
r_min = 20;
r_max = 30;
p = 0.7;
% step_r:检测的圆半径步长
% step_angle:角度步长，单位为弧度
% r_min:最小圆半径
% r_max:最大圆半径
% p:阈值，0，1 之间的数
% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% output
% hough_space:参数空间，h(a,b,r)表示圆心在(a,b)半径为 r 的圆上的点数
% hough_circl:二值图像，检测到的圆
% para:检测到的圆的圆心、半径
[m,n] = size(D1); 
size_r = round((r_max-r_min)/step_r)+1; 
size_angle = round(2*pi/step_angle); 
hough_space = zeros(m,n,size_r); 
[rows,cols] = find(D1); 
ecount = size(rows); 
% Hough 变换
% 将图像空间(x,y)对应到参数空间(a,b,r)
% a = x-r*cos(angle)
% b = y-r*sin(angle)
for i=1:ecount 
 for r=1:size_r 
 for k=1:size_angle 
 a = round(rows(i)-(r_min+(r-1)*step_r)*cos(k*step_angle)); 
 b = round(cols(i)-(r_min+(r-1)*step_r)*sin(k*step_angle)); 
 if(a>0&&a<=m&&b>0&&b<=n) 
 hough_space(a,b,r) = hough_space(a,b,r)+1; 
 end 
 end 
 end 
end 
% 搜索超过阈值的聚集点
max_para = max(max(max(hough_space))); 
index = find(hough_space>=max_para*p); 
length = size(index); 
hough_circle=zeros(m,n); 
for i=1:ecount 
 for k=1:length 
 par3 = floor(index(k)/(m*n))+1; 
 par2 = floor((index(k)-(par3-1)*(m*n))/m)+1; 
 par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m; 
if((rows(i)-par1)^2+(cols(i)-par2)^2<(r_min+(par3-1)*step_r)^2+5&&(rows(i)-par1)^2+(cols
(i)-par2)^2>(r_min+(par3-1)*step_r)^2-5) 
 hough_circle(rows(i),cols(i)) = 1; 
 end 
 end 
end 
% 处理结果 
 for k=1:length 
 par3 = floor(index(k)/(m*n))+1; 
 par2 = floor((index(k)-(par3-1)*(m*n))/m)+1; 
 par1 = index(k)-(par3-1)*(m*n)-(par2-1)*m; 
 par3 = r_min+(par3-1)*step_r; 
 fprintf(1,'Center %d %d radius %d\n',par1,par2,par3); 
 para(:,k) = [par1,par2,par3]'; 
 end 
 %%找出了很多组数据，这些数据可以分成三类
X=para'; %%使用聚类分析得到三个 x y r 信息
[cidx2,cmeans2,sumd2,D2] = kmeans(X,3,'dist','sqEuclidean');
P2 = figure;clf;
[silh2,h2] = silhouette(X,cidx2,'sqeuclidean');
% A 即为三个圆的中心坐标
A=round(cmeans2);
% 绘制圆形
figure,imshow(hough_circle)

%% 建立模板
% 将实际零件旋转角度
clc
clear
load('DATA1');
subplot(121)
imshow(D1)
I=imrotate(D1,-30);
%将旋转后的矩阵切割成 420*560
D=I(112:531,67:626);
%画出了两张图 一张为旋转前，一张为旋转后
subplot(122)
imshow(D)
%count_row 为每一行的像素计数
for i=1:420
 count_row(i,1)=sum(D(i,:)==1);
end
%找出像素最多的两行 n_row 为行号
[n1,o1]=sort(count_row,'descend'); 
n_row=o1(1:2,:);
%对于列同理 n_line 为列号 最后得出第 127 和 289
for i=1:560
 count_line(1,i)=sum(D(:,i)==1);
end
[n2,o2]=sort(count_line,'descend');
n_line=o2(:,1:2);
% 建立模板图形
% 画矩形 矩形的行列号由 rotate 中得出
model_p=zeros(420,560);
model_p(127,218:390)=1;
model_p(289,218:390)=1;
model_p(127:289,218)=1;
model_p(127:289,390)=1;
% 圆的半径及中心点
r=26; 
c1=[247,270];
c2=[212,339];
c3=[178,270];
% 420 行，560 列像素点
for i=1:420
 for j=1:560
 point=[i,j]; % 描述像素点的像素坐标
 l1=norm(c1-point); % 像素点距离圆心 c1 的距离
 l2=norm(c2-point); % 像素点距离圆心 c2 的距离
 l3=norm(c3-point); % 像素点距离圆心 c3 的距离
 % 寻找距离圆心 c1 为 r 的像素点，并使其为 1
 if r-1<=l1 && l1<=r
 model_p(i,j)=1;
 end
 % 寻找距离圆心 c2 为 r 的像素点，并使其为 1
 if r-1<=l2 && l2<=r
model_p(i,j)=1;
 end
 % 寻找距离圆心 c3 为 r 的像素点，并使其为 1
 if r-1<=l3 && l3<=r
 model_p(i,j)=1;
 end
 end
end
% 画三个圆
imshow(model_p);
% 求对角线长度
% 左上角
A1(1)=n_line(1); % 横坐标
A1(2)=n_row(2); % 纵坐标
% 右下角
B1(1)=n_line(2); % 横坐标
B1(2)=n_row(1); % 纵坐标
% 求对角线长
dis=norm(B1-A1);
% 求半对角线长
dis=dis/2;
%% 确定实际零件位置
% D1 是 DATA1 中的数据
[Y,X]=find(D1==1); % 实际零件的离散点，Y 表示行号，X 表示列号
%*************零件模板信息***************
% 通过模板建立过程得到
I=model_p; % 导入模板
% imshow(I) % 显示模板图像
[y,x]=find(I==1); % 模板中的离散点（即白点）
% 已标定模板中心点
tx=304;
ty=212.5;
% 对比模板
figure;
plot(X,Y,'R.') % 绘制实际零件图像，显示红色
hold on
plot(x-tx,y-ty,'k.') % 绘制平移之后的模板图像
% 将模板移动到坐标轴的原点位置，这一步目前看来是有必要的，
% 因为后文乘以旋转矩阵 T 的时候，旋转的基准点是坐标原点
d=[x-tx y-ty];
% 创建一个实际零件离散点列数的随机序列
r=randperm(length(x));
% 创建实际零件的像素坐标点
D=[X Y];
% 用创建的随机序列在 D1 中选取 150 个点
D=D(r(1:150),:); 
% 用创建的随机序列在模板 I 中选 150 个点，这部分在论文里可以直接说 D1 里选 150
点
d=d(r(1:150),:); 
% 在模板 I 中选了 150 个点，选取的点的数量越多，算法越准，运算速度越慢
% 确定优化边界条件
l = [-400 -400 -pi];
u = [400 400 pi]; 
x0 = [100 100 0];
TolFun = 1e-9;
TolX=1e-5;
kmax =5000;
q =0.8;
%设定退火算法的各个参数
[xo_sa,fo_sa] =Opt_Simu(@(x)myfun2(x,d,D),x0,l,u,kmax,q,TolFun)
t=xo_sa(3);
a=xo_sa(1);
b=xo_sa(2);
%退火算法得出了 x y theta 三个参数
T=[cos(t) sin(t)
 -sin(t) cos(t)];
%得出旋转矩阵
temp=[X+a Y+b]*T; 
X=round(temp(:,1)); 
Y=round(temp(:,2));
%将 D1 通过得出的 x y theta 变换到模板位置
plot(X,Y,'.')
%做第三个图

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可