- easy-rl PDF版本 笔记整理 P6 - P8
- joyrl 比对 补充 P7 - P8
- 相关 代码 整理 待整理 !!

最新版PDF下载
地址:https://github.com/datawhalechina/easy-rl/releases
国内地址(推荐国内读者使用):
链接: https://pan.baidu.com/s/1isqQnpVRWbb3yh83Vs0kbw 提取码: us6a
easy-rl 在线版本链接 (用于 copy 代码)
参考链接 2:https://datawhalechina.github.io/joyrl-book/
其它:
【勘误记录 链接】
——————
5、深度强化学习基础 ⭐️
开源内容:https://linklearner.com/learn/summary/11
——————————
蒙特卡洛: 要等到游戏结束。方差很大
时序差分: 不用等到游戏结束。更常用
不同的方法考虑了不同的假设,所以运算结果不同。


π ( a ∣ s ) = e Q ( s , a ) T ∑ a ′ ∈ A e Q ( s , a ′ ) T \pi(a|s)=\frac{e^{\frac{Q(s, a)}{T}}}{\sum\limits_{a^\prime\in \cal A}e^{\frac{Q(s, a^\prime)}{T}}} π(a∣s)=a′∈A∑eTQ(s,a′)eTQ(s,a)
T
T
T 大, 探索
T
T
T 小, 利用
经验回放 异策略
最耗时的环节: 与环境互动。

DQN 和 其它 Q-learning 学习方法的区别:
| DQN | 其它 Q-learning |
|---|---|
| 神经网络 拟合 动作值 函数 | 表格 |
| 经验回放 | 下一状态的数据 |
————————
7 个技巧: 深度 Q 网络、双深度 Q 网络、优先级经验回放的双深度 Q 网络、竞争深度 Q 网络、异步优势演员-评论员算法(A3C)、分布式 Q 函数、噪声网络。
| 序号 | 问题 | 解决方案 | 其它 |
|---|---|---|---|
| 1 | 数据存储效率;泛化 | 深度 Q 网络 (DQN) | 经验回放 + 目标网络 Q ( s t , a t ) ↔ r t + max a Q ( s t + 1 , a ) Q(s_t,a_t)\leftrightarrow r_t+\max\limits_aQ(s_{t+1},a) Q(st,at)↔rt+amaxQ(st+1,a) |
| 2 | Q 值往往被高估 | 双深度 Q 网络 (double DQN,DDQN) | Q ( s t , a t ) ↔ r t + Q ′ ( s t + 1 , arg max a Q ( s t + 1 , a ) ) Q(s_t,a_t)\leftrightarrow r_t+\textcolor{blue}{Q^\prime\Big(s_{t+1},\arg}\max\limits_aQ(s_{t+1},a)\textcolor{blue}{\Big)} Q(st,at)↔rt+Q′(st+1,argamaxQ(st+1,a)) |
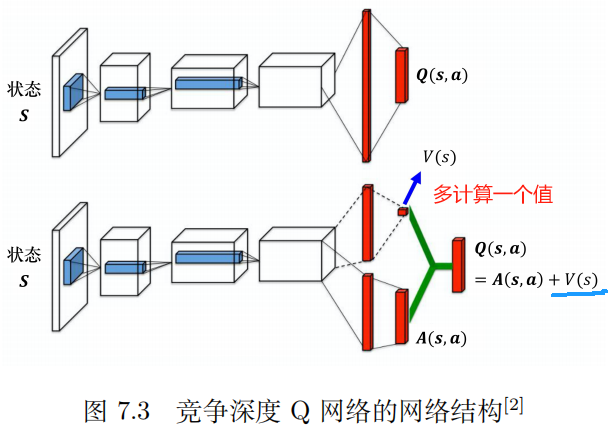
| 3 | 竞争深度 Q 网络(dueling DQN) | 第一步计算一个与输入有关的标量 V(s); 第二步计算一个向量 A(s, a) 对应每一个动作。 最后的网络将两步的结果相加,得到最终需要的 Q 值。 Q(s, a) = V(s) + A(s, a) | |
| 4 | 使用经验回放时,考虑数据间的权重大小。 | 优先级经验回放(prioritized experience replay,PER) | |
| 5 | 蒙特卡洛:方差大 | 多步方法 | 在蒙特卡洛方法和时序差分方法中取得平衡 A3C |
| 6 | 网络的权重等参数都加上一个高斯噪声 | 噪声网络(noisy net) | 类似于 ε \varepsilon ε 贪心策略,但在同一个回合里面参数是固定的 以保证 看到同一状态采取同一动作 |
| 7 | 分布式 Q 函数(distributional Q-function) | 将最终网络的输出的每一 类别的动作再进行分布操作。低估 奖励 | |
| 彩虹(rainbow) |
主网络: 更新参数, 选动作
目标网络: 某段时间固定, 计算值
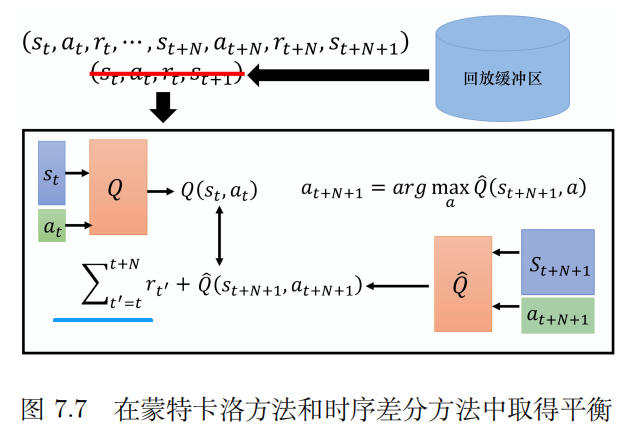
7.6 分布式 Q 函数
不易实现
Q 函数是累积奖励的期望值,所以我们算出来的 Q 值其实是一个期望值。
因为环境是有随机性的,所以在某一个状态采取某一个动作后,计算后续不同轨迹得到的奖励,得到的是一个分布。
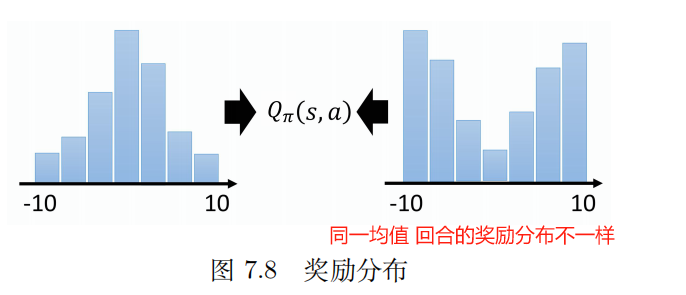
对这个 分布 求均值 得到 Q 值。
这个分布 可能对于选取 最优策略有好处, 当直接用 均值 建模时,可能会丢失重要的信息。
在原来的 Q 函数里面,假设我们只能采取 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3 这 3 个动作,我们输入一个状态,输出 3 个值。这 3 个值分别代表 3 个动作的 Q 值,但是这些 Q 值是一个分布的期望值。所以分布式 Q 函数就是直接输出分布。
假设分布的值就分布在某一个范围里面,比如 −10 ~ 10,把 −10 ~ 10 拆成一个一个的长条。例如,每一个动作的奖励空间拆成 5 个长条。假设奖励空间可以拆成 5 个长条,Q 函数的输出就是要预测我们在某一个状态采取某一个动作得到的奖励,其落在某一个长条里面的概率。所以绿色长条概率的和应该是 1,其高度代表在某一个状态采取某一个动作的时候,它落在某一个长条内的概率。绿色的代表动作 a 1 a_1 a1,红色的代表动作 a 2 a_2 a2,蓝色的代表动作 a 3 a_3 a3。
实际上在做测试的时候,我们选平均值最大的动作执行。
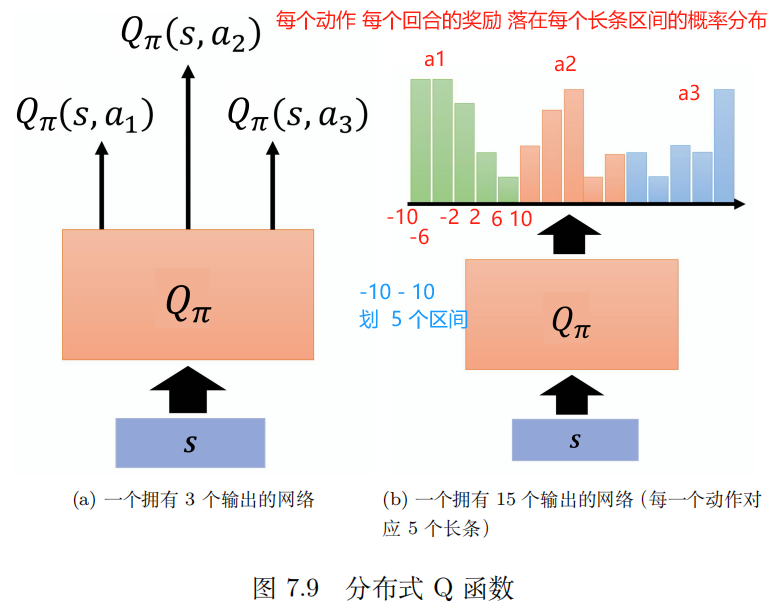
类似地, 也可对 动作值 进行分布建模。
如果 动作值 的分布方差很大,这代表采取这个动作虽然平均而言很不错,但也许风险很高,我们可以训练一个网络来规避风险。在两个动作平均值 (动作值)都差不多的情况下,也许可以选一个风险比较小 【方差小】的动作来执行,这就是分布式 Q 函数的好处。
7.7 rainbow
分数 取 中位数
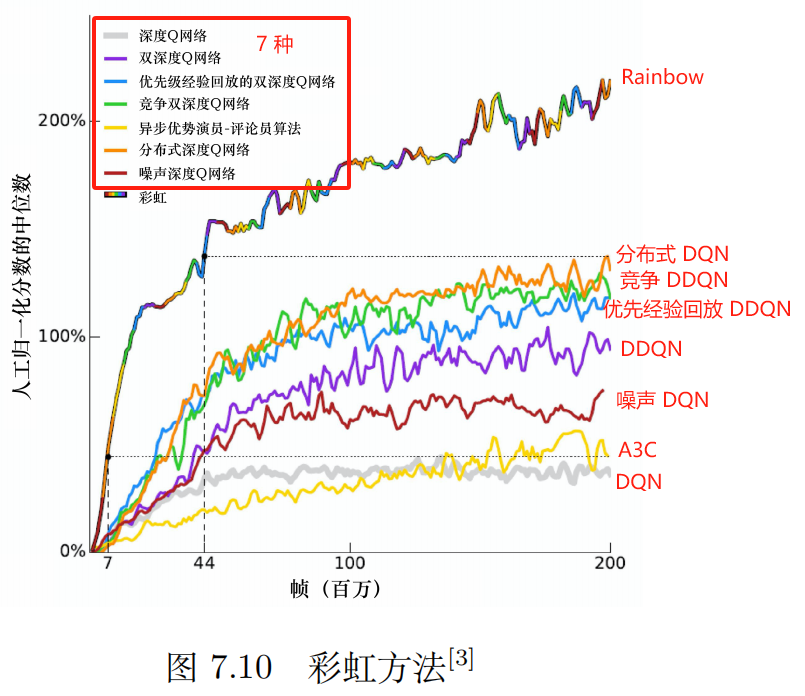
异步优势演员-评论员(asynchronous advantage actor-critic,A3C)是演员-评论员的方法,A3C 算法又被译作 异步优势动作评价算法

为什么分布式深度 Q 网络会低估奖励呢?因为分布式深度 Q 网络输出的是一个分布的范围,输出的范围不可能是无限的,我们一定会设一个限制,比如最大输出范围就是从 −10 ~10。假设得到的奖励超过 10,比如 100 怎么办?我们就当作没看到这件事。
超出设定范围的奖励值被丢弃——> 分布式深度 Q 网络低估奖励
————————
DQN 比 策略梯度 稳定
DQN 比较容易训练的原因: 只要能够估计出 Q 函数,就保证一定可以找到一个 比较好的策略。
回归问题
难以处理连续动作
| 方案 | 不足 |
|---|---|
| 采样动作 | 采样次数有限,动作不一定精确 |
| 梯度上升 | 运算量大;局部最优 |
| 设计网络架构 | 函数不能随便设置。 |
| AC演员-评论员方法 = PPO 【基于策略】+ DQN【基于价值】 |

JoyRL
梯度下降法 基于一个假设:训练集中的样本是独立同分布的。
避免训练的不稳定性
经验回放的容量不能太小,太小了会导致收集到的样本具有一定的局限性,也不能太大,太大了会失去经验本身的意义。
Double DQN 并不是每隔 C 步复制参数到目标网络,而是每次随机选择其中一个网络选择动作进行更新。
竞争Dueling DQN 算法: 优化神经网络的结构
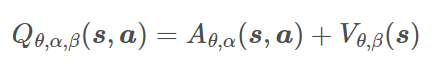
在网络模型中增加噪声层
根据经验回放中的每个样本计算出的 TD 误差赋予对应的优先级,然后在采样的时候取出优先级较大的样本。
单纯根据 TD 误差进行优先采样有可能会错过对当前网络“信息量”更大的样本。
过拟合
分布式 DQN 算法 C51 算法
【Code】OpenAI Gym 中的 CartPole-v0 车杆平衡 【连续状态空间】
参考链接 1: https://github.com/datawhalechina/joyrl-book/tree/main/notebooks
参考链接 2: https://github.com/datawhalechina/easy-rl/tree/master/notebooks
通过向左 (action=0) 或向右 (action=1) 推车让杆保持直立。每进行一个 step 就会给一个 +1 的 reward,如果无法保持平衡那么 done 等于 true,本次 episode 失败。
—— 基本信息查看
import gym
env = gym.make('CartPole-v0') # 创建环境
n_states = env.observation_space.shape[0] # 状态数
n_actions = env.action_space.n # 动作数
print(f"状态数:{n_states}, 动作数: {n_actions}")

状态数是 4 个,分别为车的位置、车的速度、杆的角度以及杆顶部的速度;
动作数为 2 个,并且是离散的向左或者向右。
state = env.reset() # 初始化环境
print(f"初始状态:{state}")

训练思路: 执行动作,环境反馈,智能体更新
交互采样 + 模型更新
本地环境:
pip install gymnasium==0.28.1
pip install gym==0.25.2
PyTorch 环境配置链接
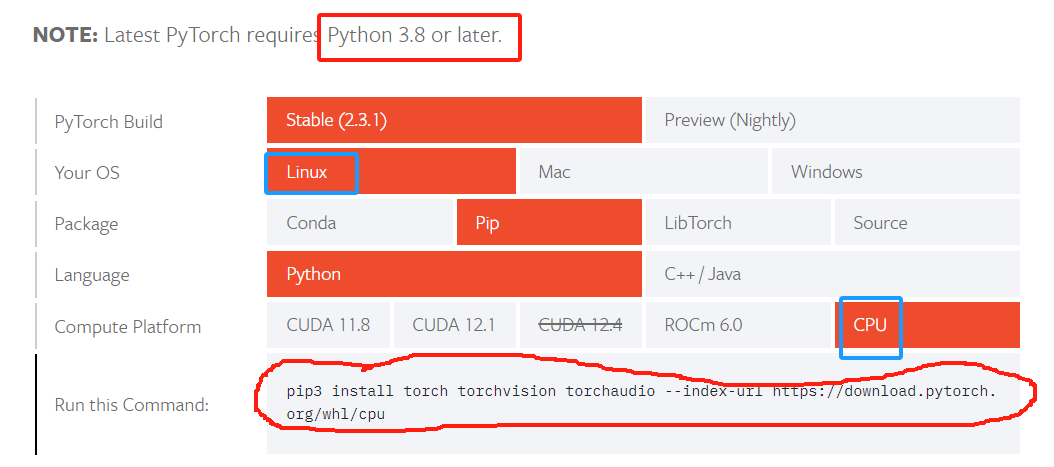
DQN_2015
论文 链接: https://sci-hub.se/10.1038/nature14236

算法: 带 经验回放 的 deep Q-learning
初始化容量为 N N N 的回放存储 D D D
用随机权重 θ \theta θ 初始化 动作-值 函数 Q Q Q
用权重 θ − = θ \theta^-=\theta θ−=θ 初始化 目标动作-值函数 Q ^ \hat Q Q^
遍历 episode = 1,M:
~~~~~~ 初始化 序列 s 1 = { x 1 } s_1=\{x_1\} s1={x1},预处理序列 ϕ 1 = ϕ ( s 1 ) \phi_1=\phi(s_1)~~~~ ϕ1=ϕ(s1) 【预处理的目的:降低输入维数并处理 Atari 2600 模拟器的一些伪影。】
~~~~~~ 对于 t = 1 , T t=1, ~T t=1, T:
~~~~~~~~~~~~ 以概率 ε \varepsilon ε 选择随机动作 a t a_t at
~~~~~~~~~~~~ 否则 a t = arg max a Q ( ϕ ( s t ) , a ; θ ) a_t=\arg\max\limits_aQ(\phi(s_t),a;\theta) at=argamaxQ(ϕ(st),a;θ)
~~~~~~~~~~~~ 在仿真器 执行动作 a t a_t at,观察 奖励 r t r_t rt 和 图像 x t + 1 x_{t+1} xt+1
~~~~~~~~~~~~ 令 s t + 1 = { s t , a t , x t + 1 } s_{t+1}=\{s_t,a_t,x_{t+1}\} st+1={st,at,xt+1},并预处理 ϕ t + 1 = ϕ ( s t + 1 ) \phi_{t+1}=\phi(s_{t+1}) ϕt+1=ϕ(st+1)
~~~~~~~~~~~~ 将 transition ( ϕ t , a t , r t , ϕ t + 1 ) (\phi_t,a_t,r_t,\phi_{t+1}) (ϕt,at,rt,ϕt+1) 存到 D D D
~~~~~~~~~~~~ 从 D D D 中随机抽样 小批次 transitions ( ϕ j , a j , r j , ϕ j + 1 ) (\phi_j,a_j,r_j,\phi_{j+1}) (ϕj,aj,rj,ϕj+1)
~~~~~~~~~~~~ 令 y j = { r j 在第 j + 1 步回合终止 r j + γ max a ′ Q ^ ( ϕ j + 1 , a ′ ; θ − ) 其它 ~~y_j=\left\{\begin{aligned}&r_j~~~~~~~~~~~~~在 第 ~j+1~步回合终止\\ &r_j+\gamma\max\limits_{a^\prime}\hat Q(\phi_{j+1}, a^\prime;\theta^-)&其它\end{aligned}\right. yj=⎩ ⎨ ⎧rj 在第 j+1 步回合终止rj+γa′maxQ^(ϕj+1,a′;θ−)其它
~~~~~~~~~~~~ 梯度下降 ( y j − Q ( ϕ j , a j ; θ ) ) 2 \Big(y_j-Q(\phi_j,a_j;\theta)\Big)^2 (yj−Q(ϕj,aj;θ))2,针对网络参数 θ \theta θ
~~~~~~~~~~~~ 每 C C C 步 重置 Q ^ = Q \hat Q=Q Q^=Q
test.py
————————————
✔ 版本 1
# pip install seaborn
# pip install gym==0.25.2
import torch.backends
import torch.nn as nn
import torch.nn.functional as F
from collections import deque
import random
import torch
import torch.optim as optim
import math
import numpy as np
import gym
import os
import argparse
import matplotlib.pyplot as plt
import seaborn as sns
#
###### 1、算法模块
# 定义 用于 拟合 Q 函数 的 神经网络 Q(s,a; θ) 输入状态, 输出动作
class MLP(nn.Module):
def __init__(self, n_states, n_actions, hidden_dim=128): # hidden_dim=128 隐藏层维度
super(MLP, self).__init__()
self.fc1 = nn.Linear(n_states, hidden_dim) # 输入层
self.fc2 = nn.Linear(hidden_dim, hidden_dim) # 隐藏层
self.fc3 = nn.Linear(hidden_dim, n_actions) # 输出层
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return self.fc3(x)
# 定义 经验回放
class ReplayBuffer(object):
def __init__(self, capacity):
self.capacity = capacity
self.buffer = deque(maxlen=self.capacity)
def push(self, transitions): # 存储 (s, a, r, s') 到 buffer 中
self.buffer.append(transitions)
def sample(self, batch_size, sequential=False): # 抽取 小批次 buffer 数据用于 更新 主网络
if batch_size > len(self.buffer):
batch_size = len(self.buffer)
if sequential: # 顺序采样
rand = random.randint(0, len(self.buffer) - batch_size)
batch = [self.buffer[i] for i in range(rand, rand + batch_size)]
return zip(*batch)
else: # 随机采样
batch = random.sample(self.buffer, batch_size)
return zip(*batch)
def __len__(self): # 返回 buffer中 存储的经验 数量
return len(self.buffer)
class DQN:
def __init__(self, model, memory, cfg): # cfg 定义了一些 超参数
self.n_actions = cfg['n_actions']
self.device = torch.device(cfg['device'])
self.gamma = cfg['gamma'] # 奖励 的 折扣因子
# ε 贪心策略 参数
self.sample_count = 0 # 用于 ε 衰减计数
self.epsilon = cfg['epsilon_start']
self.epsilon_start = cfg['epsilon_start']
self.epsilon_end = cfg['epsilon_end']
self.epsilon_decay = cfg['epsilon_decay']
self.batch_size = cfg['batch_size']
self.policy_net = model.to(self.device)
self.target_net = model.to(self.device)
# 复制参数到 目标网络
for target_param, param in zip(self.target_net.parameters(), self.policy_net.parameters()):
target_param.data.copy_(param.data)
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg['lr']) # 优化器
self.memory = memory # 经验回放
def sample_action(self, state): # 状态 s 采取 动作 a 是否是 好的策略
self.sample_count += 1
# 让 ε 随着步数指数衰减。 权衡 探索和利用
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
math.exp(-1. * self.sample_count / self.epsilon_decay)
if random.random() > self.epsilon: # ε 已经很小
with torch.no_grad():
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state)
action = q_values.max(1)[1].item() # 选择 最大动作值 对应的动作
else:
action = random.randrange(self.n_actions)
return action
## 用于 测试
@torch.no_grad()
def predict_action(self, state): # 策略已学好。 遇到状态 s 应输出 a
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state) # 学到的 Q 函数网络 输出 相应的 q 值
action = q_values.max(1)[1].item()
return action
def update(self): # 基于数据 不断更新 Q函数 的拟合模型
if len(self.memory) < self.batch_size: # 缓存器 中样本数不足 一批,不更新策
return
# 在 缓存器 中抽样 batch (s, a, r, s')
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(self.batch_size)
# 将数据 转为 tensor
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)
next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
done_batch = torch.tensor(np.float32(done_batch), device=self.device)
q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch)
next_q_values = self.target_net(next_state_batch).max(1)[0].detach()
expected_q_values = reward_batch + self.gamma * next_q_values * (1 - done_batch)
loss = nn.MSELoss()(q_values, expected_q_values.unsqueeze(1)) # 计算均方根损失
# 优化
self.optimizer.zero_grad()
loss.backward()
# Clip 防止 梯度爆炸
for param in self.policy_net.parameters():
param.grad.data.clamp_(-1,1)
self.optimizer.step()
###### 2、训练模块 和 测试模块 定义
def train(cfg, env, agent): # 训练模块
print("------开始训练------")
rewards = []
for i_ep in range(cfg['train_eps']):
ep_reward = 0 # 一个 回合 内的奖励
state = env.reset(seed=cfg['seed']) # 重置环境
for _ in range(cfg['ep_max_steps']):
action = agent.sample_action(state)
next_state, reward, done, _ = env.step(action)
agent.memory.push((state, action, reward, next_state, done))
state = next_state # 更新下一个状态
agent.update() # 更新智能体
ep_reward += reward # 累加奖励
if done:
break
if (i_ep + 1) % cfg['C'] == 0: # 智能体 目标网络更新
agent.target_net.load_state_dict(agent.policy_net.state_dict())
rewards.append(ep_reward)
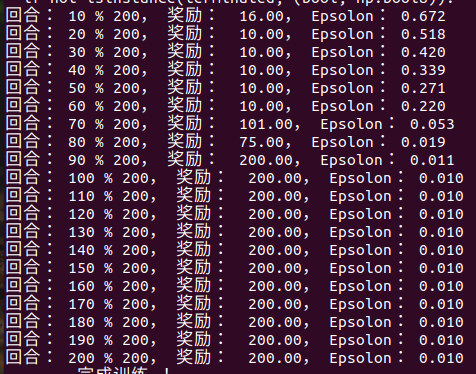
if (i_ep + 1) % 10 == 0: # 每 10 个 回合 打印
print(f"回合: {i_ep + 1} % {cfg['train_eps']}, 奖励: {ep_reward:.2f}, Epsolon: {agent.epsilon:.3f}")
print("------ 完成训练 ! ------")
env.close()
return {'rewards': rewards}
def test(cfg, env, agent): # 训练模块
print("------ 开始测试: ------")
rewards = []
for i_ep in range(cfg['test_eps']):
ep_reward = 0
state = env.reset(seed=cfg['seed']) # 重置环境
for _ in range(cfg['ep_max_steps']):
env.render() # pygame 将直接可视化
action = agent.predict_action(state)
next_state, reward, done, _ = env.step(action)
ep_reward += reward # 累加奖励
if done:
break
rewards.append(ep_reward)
print(f"回合: {i_ep + 1} / {cfg['test_eps']}, 奖励: {ep_reward :.2f}")
print("------ 完成测试 ------")
env.close()
return {'rewards': rewards} # 字典
###### 3、环境
def all_seed(env, seed = 1):
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed) # CPU
torch.cuda.manual_seed(seed) # GPU
os.environ['PYTHONHASHSEED'] = str(seed) # python
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.enabled = False
def env_agent_config(cfg):
env = gym.make(cfg['env_name'])
if cfg['seed'] != 0:
all_seed(env, seed=cfg['seed'])
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
print(f"状态数: {n_states}, 动作数: {n_actions}")
cfg.update({"n_states": n_states, "n_actions": n_actions}) # 参数配置字典 更新
model = MLP(n_states, n_actions, hidden_dim=cfg['hidden_dim'])
memory = ReplayBuffer(cfg['memory_capacity'])
agent = DQN(model, memory, cfg)
return env, agent
###### 4、参数 设置 可视化模块
def get_args(): # 超参数
parser = argparse.ArgumentParser(description="hyperparameters")
parser.add_argument('--algorithm_name', default='DQN', type=str, help='name of algorithm') # 算法名称
parser.add_argument('--env_name', default='CartPole-v0', type=str, help="name of environment")
parser.add_argument('--train_eps', default=200, type=int, help="episodes of training")
parser.add_argument('--test_eps', default = 20, type=int, help="episodes of testing")
parser.add_argument('--ep_max_steps',default = 100000,type=int,help="steps per episode, much larger value can simulate infinite steps")
parser.add_argument('--gamma',default=0.95,type=float,help="discounted factor")
parser.add_argument('--epsilon_start',default=0.95,type=float,help="initial value of epsilon")
parser.add_argument('--epsilon_end',default=0.01,type=float,help="final value of epsilon")
parser.add_argument('--epsilon_decay',default=500,type=int,help="decay rate of epsilon, the higher value, the slower decay")
parser.add_argument('--lr',default=0.0001,type=float,help="learning rate")
parser.add_argument('--memory_capacity',default=100000,type=int,help="memory capacity")
parser.add_argument('--batch_size',default=64,type=int)
parser.add_argument('--C',default=4,type=int,help="the Q of target network update after C steps of a episode")
parser.add_argument('--hidden_dim',default=256,type=int)
parser.add_argument('--device',default='cpu',type=str,help="cpu or cuda")
parser.add_argument('--seed',default=10,type=int,help="seed")
args = parser.parse_args([])
args = {**vars(args)}
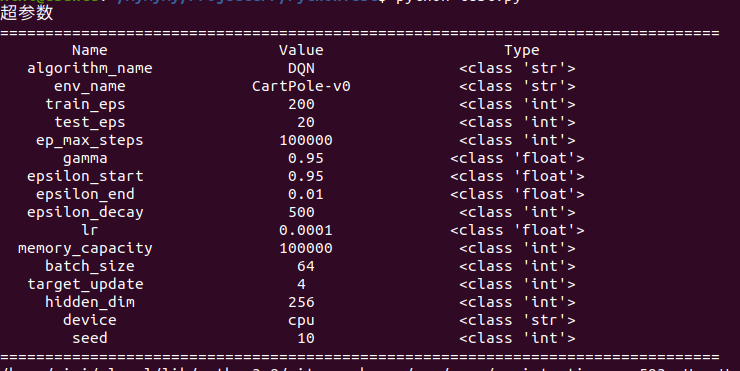
# 打印 超参数
print("超参数")
print(''.join(['=']*80))
tplt = "{:^20}\t{:^20}\t{:^20}"
print(tplt.format("Name", "Value", "Type"))
for k,v in args.items():
print(tplt.format(k,v,str(type(v))))
print(''.join(['=']*80))
return args
def smooth(data, weight=0.9): # 平滑曲线
last = data[0]
smoothed = []
for point in data:
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值
smoothed.append(smoothed_val)
last = smoothed_val
return smoothed # 返回计算好的平滑数据
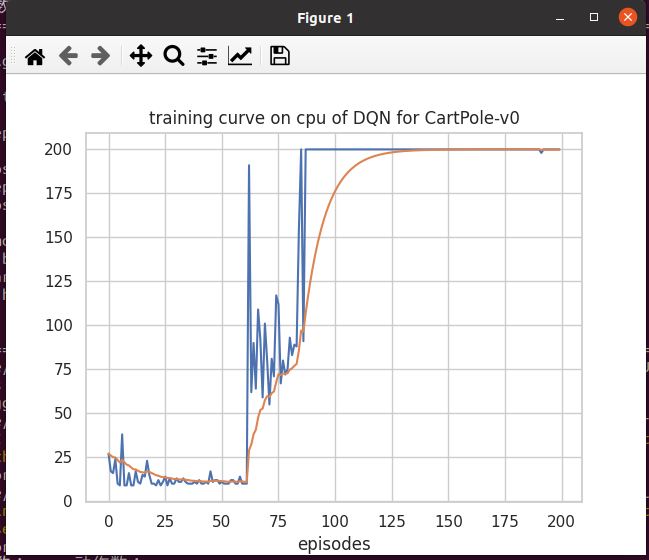
def plot_rewards(rewards, cfg, tag='train'): # 训练过程的奖励 可视化
sns.set(style='whitegrid') # 可设置 seaborn 绘图风格
plt.figure()
plt.title(f"{tag}ing curve on {cfg['device']} of {cfg['algorithm_name']} for {cfg['env_name']}") # 算法名称 环境名称
plt.xlabel('episodes')
plt.plot(rewards, label='rewards')
plt.plot(smooth(rewards), label='smoothed')
# plt.legend()
plt.show()
###### 5、训练 和 测试
cfg = get_args() # 获取参数
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag = "train")
# 测试
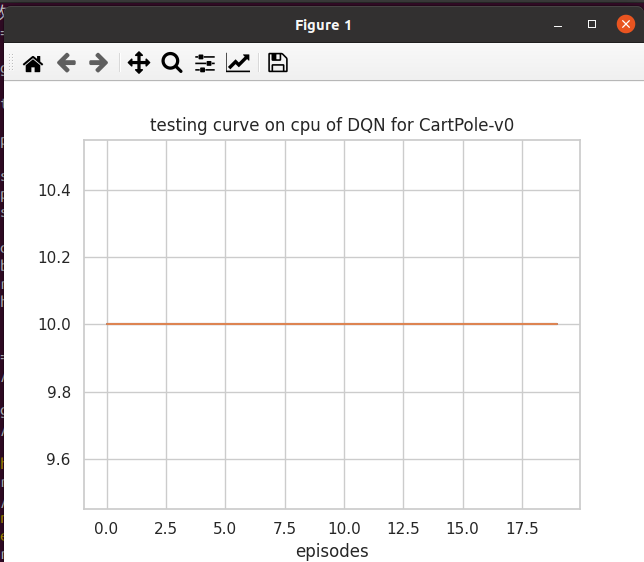
res_dic = test(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag="test")
待改版本
拟改成 gymnasium 版本, 目前版本仍有报错
❌
import torch.nn as nn
import torch.nn.functional as F
from collections import deque
import random
import torch
import torch.optim as optim
import math
import numpy as np
import gymnasium as gym
import os
import argparse
import matplotlib.pyplot as plt
import seaborn as sns
#
###### 1、算法模块
# 定义 用于 拟合 Q 函数 的 神经网络 Q(s,a; θ) 输入状态, 输出动作
class MLP(nn.Module):
def __init__(self, n_states, n_actions, hidden_dim=128): # hidden_dim=128 隐藏层维度
super(MLP, self).__init__()
self.fc1 = nn.Linear(n_states, hidden_dim) # 输入层
self.fc2 = nn.Linear(hidden_dim, hidden_dim) # 隐藏层
self.fc3 = nn.Linear(hidden_dim, n_actions) # 输出层
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
return self.fc3(x)
# 定义 经验回放
class ReplayBuffer(object):
def __init__(self, capacity):
self.capacity = capacity
self.buffer = deque(maxlen=self.capacity)
def push(self, transitions): # 存储 (s, a, r, s') 到 buffer 中
self.buffer.append(transitions)
def sample(self, batch_size, sequential=False): # 抽取 小批次 buffer 数据用于 更新 主网络
if batch_size > len(self.buffer):
batch_size = len(self.buffer)
if sequential: # 顺序采样
rand = random.randint(0, len(self.buffer) - batch_size)
batch = [self.buffer[i] for i in range(rand, rand + batch_size)]
return zip(*batch)
else: # 随机采样
batch = random.sample(self.buffer, batch_size)
return zip(*batch)
def __len__(self): # 返回 buffer中 存储的经验/数据 数量
return len(self.buffer)
class DQN:
def __init__(self, model, memory, cfg): # cfg 定义了一些 超参数
self.n_actions = cfg['n_actions']
self.device = torch.device(cfg['device'])
self.gamma = cfg['gamma'] # 奖励 的 折扣因子
# ε 贪心策略 参数
self.sample_count = 0 # 用于 ε 衰减计数
self.epsilon_start = cfg['epsilon_start']
self.epsilon_end = cfg['epsilon_end']
self.epsilon_decay = cfg['epsilon_decay']
self.batch_size = cfg['batch_size']
self.policy_net = model.to(self.device)
self.target_net = model.to(self.device)
# 复制参数到 目标网络
for target_param, param in zip(self.target_net.parameters(), self.policy_net.parameters()):
target_param.data.copy_(param.data)
self.optimizer = optim.Adam(self.policy_net.parameters(), lr=cfg['lr']) # 优化器
self.memory = memory # 经验回放
def sample_action(self, state): # 状态 s 执行 动作 a 是否是 好的策略
self.sample_count += 1
# 让 ε 随着步数指数衰减。 权衡 探索和利用
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * \
math.exp(-1. * self.sample_count / self.epsilon_decay)
if random.random() > self.epsilon: # ε 已经很小
with torch.no_grad():
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state)
action = q_values.max(1)[1].item() # 选择 最大动作值 对应的动作
else:
action = random.randrange(self.n_actions)
return action
## 用于 测试
@torch.no_grad()
def predict_action(self, state): # 策略已学好。 遇到状态 s 应输出 a
state = torch.tensor(state, device=self.device, dtype=torch.float32).unsqueeze(dim=0)
q_values = self.policy_net(state) # 学到的 Q 函数网络 输出 相应的 q 值
action = q_values.max(1)[1].item()
return action
def update(self): # 基于数据 不断更新 Q函数 的拟合模型
if len(self.memory) < self.batch_size: # 缓存器 中样本数不足 一批,不更新策
return
# 在 缓存器 中抽样 batch (s, a, r, s')
state_batch, action_batch, reward_batch, next_state_batch, done_batch = self.memory.sample(self.batch_size)
# 将数据 转为 tensor
state_batch = torch.tensor(np.array(state_batch), device=self.device, dtype=torch.float)
action_batch = torch.tensor(action_batch, device=self.device).unsqueeze(1)
reward_batch = torch.tensor(reward_batch, device=self.device, dtype=torch.float)
next_state_batch = torch.tensor(np.array(next_state_batch), device=self.device, dtype=torch.float)
done_batch = torch.tensor(np.float32(done_batch), device=self.device)
q_values = self.policy_net(state_batch).gather(dim=1, index=action_batch)
next_q_values = self.target_net(next_state_batch).max(1)[0].detach() # 最大的 q
expected_q_values = reward_batch + self.gamma * next_q_values * (1 - done_batch) # done_batch 记录 是否是批次的结束。若是,要更新 主网络
loss = nn.MSELoss()(q_values, expected_q_values) # 计算均方根损失
# 优化
self.optimizer.zero_grad()
loss.backward()
# Clip 防止 梯度爆炸
for param in self.policy_net.parameters():
param.grad.data.clamp_(-1,1)
self.optimizer.step()
###### 2、训练模块 和 测试模块 定义
def train(cfg, env, agent): # 训练模块
print("------开始训练------")
rewards = []
steps = []
for i_ep in range(cfg['train_eps']):
ep_reward = 0 # 一个 回合 内的奖励
ep_step = 0
state, info = env.reset(seed=cfg['seed']) # 重置环境
for _ in range(cfg['ep_max_steps']):
ep_step += 1
action = agent.sample_action(state)
next_state, reward, terminated, truncated, info = env.step(action)
agent.memory.push((state, action, reward, next_state, terminated))
state = next_state # 更新下一个状态
agent.update() # 更新智能体
ep_reward += reward # 累加奖励
if terminated:
break
if (i_ep + 1) % cfg['target_update'] == 0: # 智能体 目标网络更新 每 C 步 更新 目标网络
agent.target_net.load_state_dict(agent.policy_net.state_dict())
steps.append(ep_reward)
rewards.append(ep_reward)
if (i_ep + 1) % 10 == 0: # 每 10 个 回合 打印
print(f"回合: {i_ep + 1} % {cfg['train_eps']}, 奖励: {ep_reward:.2f}, Epsolon: {agent.epsilon:.3f}")
print("------ 完成训练 ! ------")
env.close()
return {'rewards': rewards}
def test(cfg, env, agent): # 训练模块
print("------ 开始测试: ------")
# 测试时 不用 计步数了
rewards = []
for i_ep in range(cfg['test_eps']):
ep_reward = 0
state, info = env.reset(seed=cfg['seed']) # 重置环境
for _ in range(cfg['ep_max_steps']):
action = agent.predict_action(state)
next_state, reward, terminated, truncated, info = env.step(action)
ep_reward += reward # 累加奖励
if terminated:
break
rewards.append(ep_reward)
print(f"回合: {i_ep + 1} / {cfg['test_eps']}, 奖励: {ep_reward :.2f}")
print("------ 完成测试 ------")
env.close()
return {'rewards': rewards} # 字典
###### 3、环境
def all_seed(env, seed = 1):
# env.seed(seed)
np.random.seed(seed)
random.seed(seed)
torch.manual_seed(seed) # CPU
torch.cuda.manual_seed(seed) # GPU
os.environ['PYTHONHASHSEED'] = str(seed) # python
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.enabled = False
def env_agent_config(cfg):
env = gym.make(cfg['env_name'])
if cfg['seed'] != 0:
all_seed(env, seed=cfg['seed'])
n_states = env.observation_space.shape[0]
n_actions = env.action_space.n
print(f"状态数: {n_states}, 动作数: {n_actions}")
cfg.update({"n_states": n_states, "n_actions": n_actions}) # 参数配置字典 更新
model = MLP(n_states, n_actions, hidden_dim=cfg['hidden_dim'])
memory = ReplayBuffer(cfg['memory_capacity'])
agent = DQN(model, memory, cfg)
return env, agent
###### 4、参数 设置 可视化模块
def get_args(): # 超参数
parser = argparse.ArgumentParser(description="hyperparameters")
parser.add_argument('--algorithm_name', default='DQN', type=str, help='name of algorithm') # 算法名称
parser.add_argument('--env_name', default='CartPole-v1', type=str, help="name of environment")
parser.add_argument('--train_eps', default=200, type=int, help="episodes of training")
parser.add_argument('--test_eps', default = 20, type=int, help="episodes of testing")
parser.add_argument('--ep_max_steps',default = 100000,type=int,help="steps per episode, much larger value can simulate infinite steps")
parser.add_argument('--gamma',default=0.95,type=float,help="discounted factor")
parser.add_argument('--epsilon_start',default=0.95,type=float,help="initial value of epsilon")
parser.add_argument('--epsilon_end',default=0.01,type=float,help="final value of epsilon")
parser.add_argument('--epsilon_decay',default=500,type=int,help="decay rate of epsilon, the higher value, the slower decay")
parser.add_argument('--lr',default=0.0001,type=float,help="learning rate")
parser.add_argument('--memory_capacity',default=100000,type=int,help="memory capacity")
parser.add_argument('--batch_size',default=64,type=int)
parser.add_argument('--target_update',default=4,type=int) # 伪代码里的 C
parser.add_argument('--hidden_dim',default=256,type=int)
parser.add_argument('--device',default='cpu',type=str,help="CPU or GPU")
parser.add_argument('--seed',default=10,type=int,help="seed")
args = parser.parse_args([])
args = {**vars(args)}
# 打印 超参数
print("超参数")
print(''.join(['=']*80))
tplt = "{:^20}\t{:^20}\t{:^20}"
print(tplt.format("Name", "Value", "Type"))
for k, v in args.items():
print(tplt.format(k,v,str(type(v))))
print(''.join(['=']*80))
return args
def smooth(data, weight=0.9): # 平滑曲线
last = data[0]
smoothed = []
for point in data:
smoothed_val = last * weight + (1 - weight) * point # 计算平滑值
smoothed.append(smoothed_val)
last = smoothed_val
return smoothed # 返回计算好的平滑数据
def plot_rewards(rewards, cfg, tag='train'): # 训练过程的奖励 可视化
sns.set(style='whitegrid') # 可设置 seaborn 绘图风格
plt.figure()
plt.title(f"{tag}ing curve on {cfg['device']} of {cfg['algorithm_name']} for {cfg['env_name']}") # 算法名称 环境名称
plt.xlabel('episodes')
plt.plot(rewards, label='rewards')
plt.plot(smooth(rewards), label='smoothed')
plt.show()
###### 5、训练 和 测试
cfg = get_args() # 获取参数
env, agent = env_agent_config(cfg)
res_dic = train(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag = "train")
# 测试
res_dic = test(cfg, env, agent)
plot_rewards(res_dic['rewards'], cfg, tag="test")
▢ Double DQN_2016
论文 PDF 链接:Deep Reinforcement Learning with Double Q-learning
来自 https://arxiv.org/pdf/1511.06581 的伪代码

算法: Double DQN
输入:空的回放缓存 replay buffer D \cal D D、初始网络权重 θ \theta θ、目标网络权重 θ − = θ \theta^-=\theta θ−=θ
~~~~~~~~~ 回放缓存 replay buffer 的最大容量 N r N_r Nr,训练 batch-size N b N_b Nb 、目标网络的替换频次 N − N^- N−
遍历 episode e ∈ { 1 , 2 , ⋯ , M } e\in\{1, 2,\cdots,M\} e∈{1,2,⋯,M}:
~~~~~~ 初始化 帧序列 x ← ( ) \bf x\leftarrow() x←(),
~~~~~~ 对于 t ∈ { 0 , 1 , ⋯ } t\in\{0,1, \cdots\} t∈{0,1,⋯}:
~~~~~~~~~~~~ 令 状态 s ← x s\leftarrow\bf x s←x,抽样动作 a ∼ π B a\sim\pi_{\cal B}~~~ a∼πB 【必须从 buffer里抽取?——>模拟 均匀分布】
~~~~~~~~~~~~ 给定 ( s , a ) (s, a) (s,a), 根据 E \mathcal{E} E 抽取下一个环境 x t x^t xt, 得到奖励 r r r, 将 x t x^t xt 添加到 x \bf x x 中。
~~~~~~~~~~~~ 如果 ∣ x ∣ > N f |{\bf x}|>N_f ∣x∣>Nf, 删掉 x {\bf x} x 中最旧的帧 x t min x_{t_{\min}}~~~ xtmin 【设的阈值?】
~~~~~~~~~~~~ 令 s ′ ← x s^\prime\leftarrow\bf x s′←x, 将 ( s , a , r , s ′ ) (s, a, r, s^\prime) (s,a,r,s′) 添加到 D \cal D D,若是 ∣ D ∣ ≥ N r |{\cal D}|\geq N_r ∣D∣≥Nr, 替换最旧的数据
~~~~~~~~~~~~ 抽样长度为 N b N_b Nb 的小批量元组 ( s , a , r , s ′ ) ∼ U n i f ( D ) (s, a,r,s^\prime)\sim {\rm Unif}(\cal D)~~~~ (s,a,r,s′)∼Unif(D) 【近似 均匀分布】
~~~~~~~~~~~~ 对于长度为 N b N_b Nb 的元组中的每一个样本计算 目标值
~~~~~~~~~~~~ 令 y j = { r s ′ 是 e p i s o d e 终点 r + γ Q ( s ′ , arg max a ′ Q ( s ′ , a ′ ; θ ) ; θ − ) 其它 ~~y_j=\left\{\begin{aligned}&r ~~~~~~~~~~~~s^\prime ~是~{\rm episode}~ 终点\\ &r+\gamma Q\Big(s^\prime,\arg\max\limits_{a^\prime}Q(s^\prime, a^\prime;\theta);\theta^-\Big)~~~~~~其它\end{aligned}\right. yj=⎩ ⎨ ⎧r s′ 是 episode 终点r+γQ(s′,arga′maxQ(s′,a′;θ);θ−) 其它
~~~~~~~~~~~~ 对损失 ∣ ∣ y j − Q ( s , a ; θ ) ∣ ∣ 2 ~||y_j-Q(s,a;\theta)||^2~ ∣∣yj−Q(s,a;θ)∣∣2 梯度下降
~~~~~~~~~~~~ 每 N − N^- N− 步 替换目标参数 θ − ← θ ~\theta^-\leftarrow\theta θ−←θ
$\mathcal{E}$
E
~~~\mathcal{E}
E
test.py
在这里插入代码片
▢ 竞争 Dueling DQN 算法_2016
论文 PDF 链接: Dueling Network Architectures for Deep Reinforcement Learning
Q ( s , a ; θ , α , β ) = V ( s ; θ , β ) + ( A ( s , a ; θ , α ) − 1 ∣ A ∣ ∑ a ′ A ( s , a ′ ; θ , α ) ) Q(s,a;\theta,\alpha,\beta)=V(s;\theta,\beta)+\Big(A(s,a;\theta,\alpha)-\frac{1}{|\mathcal A|}\sum\limits_{a^\prime}A(s,a^\prime;\theta,\alpha)\Big) Q(s,a;θ,α,β)=V(s;θ,β)+(A(s,a;θ,α)−∣A∣1a′∑A(s,a′;θ,α))
- θ \theta θ 是卷积层参数。 α \alpha α 和 β \beta β 分别是两个输出全连接层的参数
- 状态-动作值函数 Q ( s , a ; θ , α , β ) Q(s,a;\theta,\alpha,\beta) Q(s,a;θ,α,β) 是真实 Q Q Q 函数的参数化估计
- V ( s ; θ , β ) V(s;\theta,\textcolor{blue}{\beta}) V(s;θ,β) 不是 状态值 函数好的估计
- 取决于状态的动作优势函数 A ( s , a ; θ , α ) A(s,a;\theta,\textcolor{blue}{\alpha}) A(s,a;θ,α) 也不是 优势函数的合理估计。每个行动重要性的度量
▢ Noisy DQN_2018
论文 PDF 链接:Noisy Networks for Exploration

▢ PER DQN_2016
论文 PDF 链接:Prioritized Experience Replay
▢ 分布式 DQN_2017
论文 PDF 链接:A Distributional Perspective on Reinforcement Learning







![[每周一更]-(第103期):GIT初始化子模块](https://img-blog.csdnimg.cn/direct/9c71a0fe979140c29433620914d491af.jpeg#pic_center)