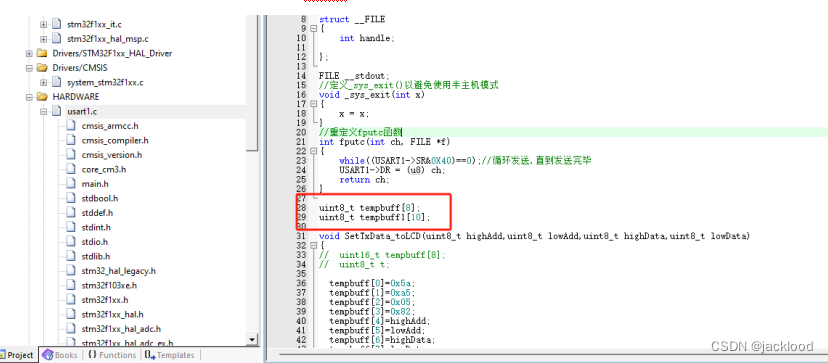
1、如图结构,想在multimenu.C和usart1.c中使用变量tempbuff


于是,就将使用的代码移动了过来,为SetTxData1_toLCD(0x00,0x01);和UserUart1Send( tempbuff1,sizeof(tempbuff1));,编译后提示错误如下:

communication_protocol\communication_protocol.axf: Error: L6218E: Undefined symbol tempbuff (referred from main.o).
提示未定义,原因是只在usart1.h中做了extern的声明,如图
此extern的声明只是告知其他程序文件可以调用usart1.h头文件来使用tempbuff[8];和tempbuff1[10];,但是还必须要在usart.c中定义这两个变量才行,从而能编译通过。
另外,如果是函数在别的文件中使用,可以不用加extern,如void UserUart1Send(uint8_t *send_data,uint8_t send_len);