三、学习分类
1.分类的目的
找到一条线把白点和黑点分开。这条直线是使权重向量成为法线向量的直线。(解释见下图)
直线的表达式为:
ω
⋅
x
=
∑
i
=
1
n
ω
i
⋅
x
i
=
0
\omega·x = \sum_{i=1}^n\omega_i · x_i = 0
ω⋅x=i=1∑nωi⋅xi=0
- ω \omega ω是权重向量
- 权重向量就是我们想要知道的未知参数
- 他和回归中的 θ \theta θ是一样的
举个例子:
ω
⋅
x
=
(
1
,
1
)
⋅
(
x
1
,
x
2
)
=
ω
1
⋅
x
1
+
ω
2
⋅
x
2
=
x
1
+
x
2
=
0
\omega·x = (1,1)·(x_1,x_2) = \omega_1·x_1 + \omega_2·x_2 = x_1 + x_2 = 0
ω⋅x=(1,1)⋅(x1,x2)=ω1⋅x1+ω2⋅x2=x1+x2=0
对应的图像:
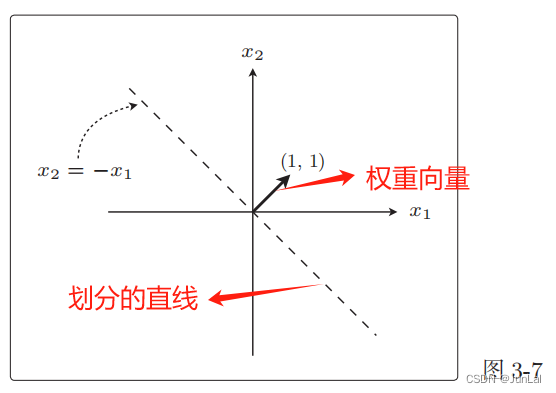
权重向量和这条直线是垂直的。
2.感知机
1定义
将权重向量用作参数,创建更新表达式来更新参数。基本做法是和回归相同的,感知机是接受多个输入后将每个值与各自的权重相乘,最后输出总和的模型。
感知机的表示:
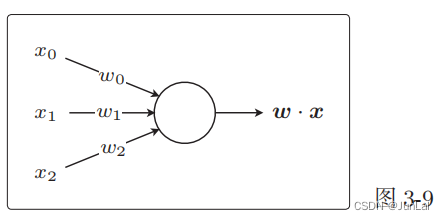
2判别函数
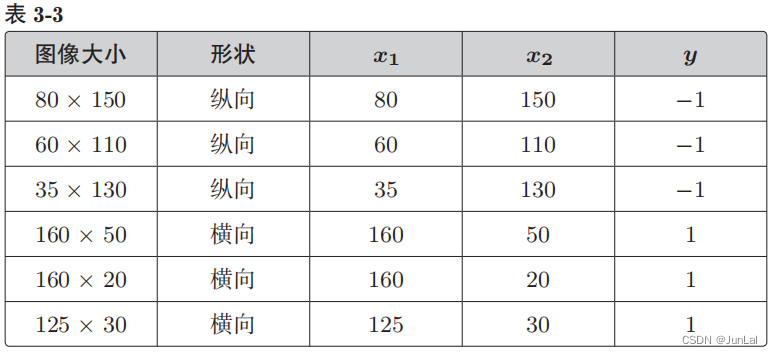
根据参数向量 x 来判断图像是横向还是纵向的函数,即返回 1 或者 −1 的函数
f
w
(
x
)
f_w(x)
fw(x)的定义如下。这个函数被称为判别函数。
f
ω
=
{
1
,
(
ω
⋅
x
≥
0
)
−
1
,
(
ω
⋅
x
<
0
)
f_\omega= \begin{cases}~1,~~~~(\omega·x\ge0) \\-1,~~(\omega·x\lt0)\end{cases}
fω={ 1, (ω⋅x≥0)−1, (ω⋅x<0)
其实,
ω
⋅
x
\omega · x
ω⋅x还可以写成
ω
⋅
x
=
∣
ω
∣
⋅
∣
x
∣
⋅
cos
θ
\omega · x = |\omega| ·| x|·\cos \theta
ω⋅x=∣ω∣⋅∣x∣⋅cosθ,那么我们可以推断出
ω
⋅
x
\omega · x
ω⋅x的正负只跟
θ
\theta
θ有关系。
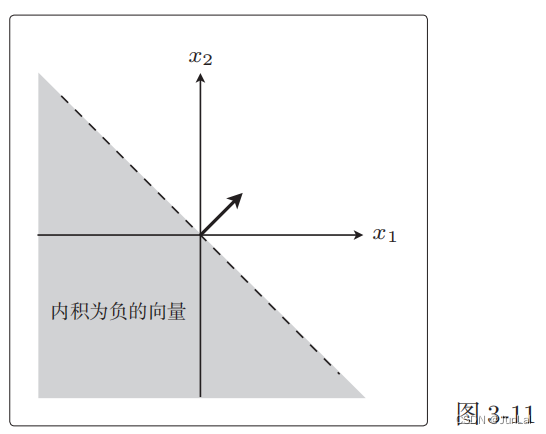
向量与权重向量 ω \omega ω之间的夹角为 θ,在 90°<θ< 270° cos θ \cos \theta cosθ为负,所以在 90°<θ< 270°范围内的所有向量都满足内积为负。
3权重向量的更新表达式
ω : = { ω + y ( i ) x ( i ) , f ω ( x ( i ) ) ≠ y ( i ) ω , f ω ( x ( i ) ) = y ( i ) \omega:= \begin{cases} \omega + y^{(i)}x^{(i)},~~~f_\omega(x^{(i)})\ne y^{(i)} \\ \omega,~~~~~~~~~~~~~~~~~~~f_\omega(x^{(i)}) = y^{(i)} \end{cases} ω:={ω+y(i)x(i), fω(x(i))=y(i)ω, fω(x(i))=y(i)
- i指的是训练数据的索引,也就是第i个训练数据的意思
- f ω ( x ( i ) ) = y ( i ) f_\omega(x^{(i)}) = y^{(i)} fω(x(i))=y(i)时说明判别函数的分类结果是准确的,此时不用更新 ω \omega ω
- f ω ( x ( i ) ) ≠ y ( i ) f_\omega(x^{(i)})\ne y^{(i)} fω(x(i))=y(i)时说明判别函数的分类结果不正确,此时需要更新表达式
下面来解释为什么
f
ω
(
x
(
i
)
)
≠
y
(
i
)
f_\omega(x^{(i)})\ne y^{(i)}
fω(x(i))=y(i)时需要更新表达式
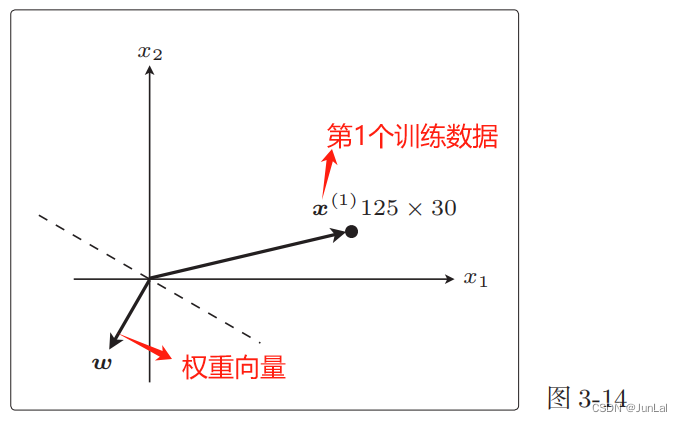
现在权重向量
ω
\omega
ω 和训练数据的向量
x
(
1
)
x^{(1)}
x(1)二者的方向几乎相反,
ω
\omega
ω和
x
(
1
)
x^{(1)}
x(1)之间的夹角 θ 的范围是 90◦ <θ< 270◦ ,内积为负。
也就是说,判别函数
f
ω
(
x
(
1
)
)
f_\omega(x^{(1)})
fω(x(1))的结果为 −1。

f ω ( x ( 1 ) ) ≠ y ( 1 ) f_\omega(x^{(1)}) \ne y^{(1)} fω(x(1))=y(1),说明分类失败。
更新: 由于 y ( 1 ) = 1 ,故 ω + y ( 1 ) x ( 1 ) = ω + x ( 1 ) 由于y^{(1)} = 1,故\omega + y^{(1)}x^{(1)} = \omega + x^{(1)} 由于y(1)=1,故ω+y(1)x(1)=ω+x(1)
图像的变化更明显一些:
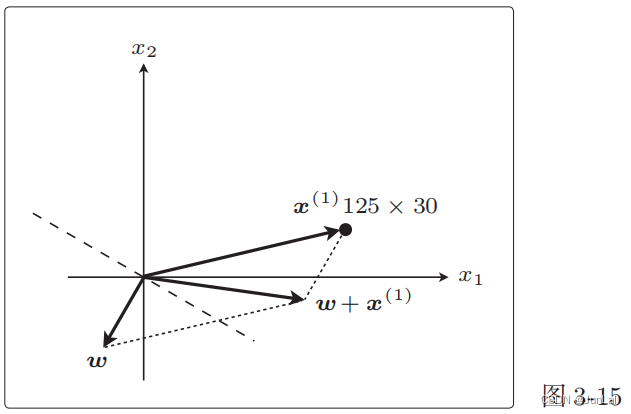
这个 ω + x ( 1 ) \omega + x^{(1)} ω+x(1)就是下一个新的 ω \omega ω,相当于把原来的线旋转了一下。
刚才处理的是标签值 y = 1 的情况,而对于 y = −1 的情况,只是更新表达式的向量加法变成了减法。本质的做法都是在分类
失败时更新权重向量,使得直线旋转相应的角度。这样重复更新所有的参数,就是感知机的学习方法。
4感知机的缺点
只能解决线性可分的问题。线性可分指的就是能够使用直线分类的情况。
之前提到的感知机也被称为简单感知机或单层感知机,是很弱的模型。既然有单层感知机,那么就会有多层感知机。实际上多层感知机就是神经网络。
3.逻辑回归
与感知机的不同之处在于,它是把分类作为概率来考虑的,举个例子,x是横向的概率是80%,而感知机的结果是A是横向。然后判别函数的两个值设置为0和1。
f
ω
=
{
1
,
(
ω
⋅
x
≥
0
)
0
,
(
ω
⋅
x
<
0
)
f_\omega= \begin{cases}1,~~~(\omega·x\ge0) \\0,~~~(\omega·x\lt0)\end{cases}
fω={1, (ω⋅x≥0)0, (ω⋅x<0)
1 Sigmoid函数
能够将未知数据分类为某个类别的函数
f
θ
(
x
)
f_\theta(x)
fθ(x) ,类似感知机的判别函数
f
ω
(
x
)
f_\omega(x)
fω(x),在这里我们把
f
θ
(
x
)
f_\theta(x)
fθ(x)当作概率,对应的前面举的横向的例子。
f
θ
(
x
)
=
80
%
f_\theta(x) = 80\%
fθ(x)=80% 表示的就是x是横向图像的概率是80%。
f
θ
(
x
)
=
1
1
+
e
(
−
θ
T
x
)
f_\theta(x) = \frac{1}{1+e^{(-\theta^Tx)}}
fθ(x)=1+e(−θTx)1
函数图像
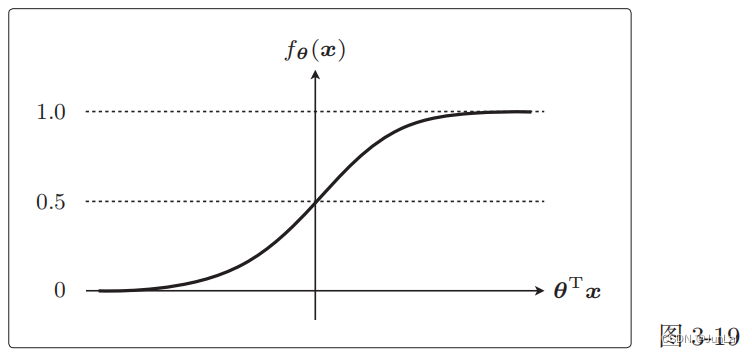
两个特征
- θ T x = 0 \theta^Tx = 0 θTx=0时, f θ ( x ) = 0.5 f_\theta(x) = 0.5 fθ(x)=0.5
- 0 < f θ ( x ) ≤ 1 0\lt f_\theta(x)\le1 0<fθ(x)≤1
2 决策边界
把
f
θ
(
x
)
f_\theta(x)
fθ(x)当作概率,我们还可以有另一种等价的表达式
f
θ
(
x
)
=
P
(
y
=
1
∣
x
)
f_\theta(x) = P(y=1|x)
fθ(x)=P(y=1∣x)
P
(
y
=
1
∣
x
)
P(y=1|x)
P(y=1∣x)表示给出x数据时y=1的概率。
假如 f θ ( x ) = 0.7 f_\theta(x) = 0.7 fθ(x)=0.7,我们会把x分类为横向。 f θ ( x ) = 0.2 f_\theta(x) = 0.2 fθ(x)=0.2,横向的概率为20%,纵向的概率为80%,这种状态可以分类为纵向。这里我们就是以0.5为阈值,然后把$f_\theta(x) $的结果与其比较,从而得到分类的结果。
即你的分类表达式为:
y
=
{
1
,
(
f
θ
(
x
)
≥
0.5
)
0
,
(
f
θ
(
x
)
<
0.5
)
y= \begin{cases}1,~~~(f_\theta(x)\ge0.5) \\0,~~~(f_\theta(x)\lt0.5)\end{cases}
y={1, (fθ(x)≥0.5)0, (fθ(x)<0.5)
从图像中可以看出
f
θ
(
x
)
≥
0.5
f_\theta(x) \ge 0.5
fθ(x)≥0.5时,
θ
T
x
≥
0
\theta^Tx\ge0
θTx≥0,反之。
所以分类表达式可以写成:
y
=
{
1
,
(
θ
T
x
≥
0
)
0
,
(
θ
T
x
<
0
)
y= \begin{cases}1,~~~(\theta^Tx\ge0) \\0,~~~(\theta^Tx\lt0)\end{cases}
y={1, (θTx≥0)0, (θTx<0)
假设有一个训练数据为
θ
=
[
θ
0
θ
1
θ
2
]
=
[
−
100
2
1
]
,
x
=
[
1
x
1
x
2
]
(2)
\theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \end{bmatrix} \tag{2} = \begin{bmatrix} -100\\2\\1 \end{bmatrix} , x = \begin{bmatrix} 1\\x_1\\x_2 \end{bmatrix}
θ=
θ0θ1θ2
=
−10021
,x=
1x1x2
(2)
所以
θ
T
x
=
−
100
⋅
1
+
2
x
1
+
x
2
≥
0
→
x
2
≥
−
2
x
2
+
100
\theta^Tx = -100\cdot1+2x_1+x_2\ge0 \to x_2\ge -2x_2+100
θTx=−100⋅1+2x1+x2≥0→x2≥−2x2+100
对应的图像为
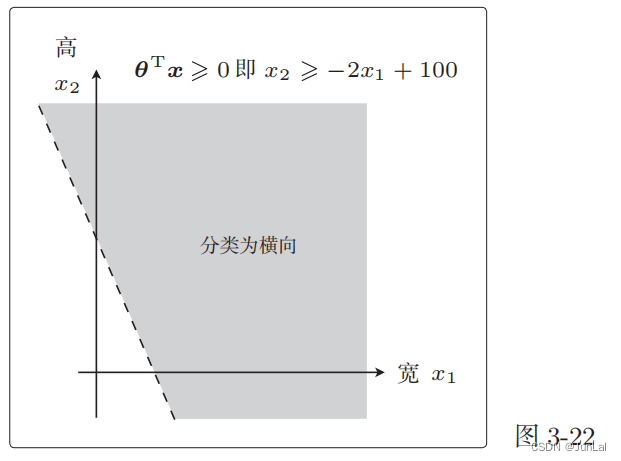
将 θ T x = 0 \theta^Tx = 0 θTx=0 这条直线作为边界线,就可以把这条线两侧的数据分类为横向和纵向。
这样用于数据分类的直线称为决策边界。
然后的做法和回归一样,为了求得正确的参数 θ 而定义目标函数,进行微分,然后求出参数的更新表达式。
4.似然函数(解决逻辑回归中参数更新表达式问题)
P(y = 1|x) 是图像为横向的概率,P(y = 0|x) 是图像为纵向的概率
- y = 1 的时候,我们希望概率 P(y = 1|x) 是最大的
- y = 0 的时候,我们希望概率 P(y = 0|x) 是最大的
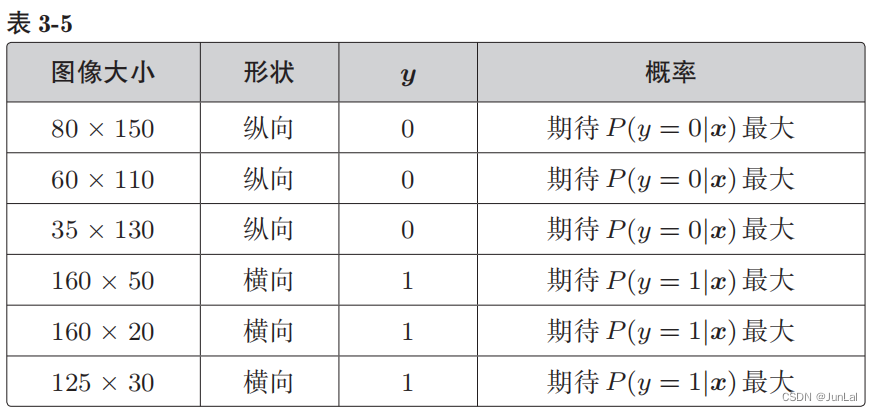
假定所有的训练数据都是互不影响、独立发生的,这种情况下整体的概率就可以用下面的联合概率来表示
L
(
θ
)
=
P
(
y
(
1
)
=
0
∣
x
(
1
)
)
P
(
y
(
2
)
=
0
∣
x
(
2
)
)
⋅
⋅
⋅
P
(
y
(
6
)
=
1
∣
x
(
6
)
)
L(θ) = P(y^{(1)} = 0 | x^{(1)})P(y^{(2)} = 0 | x^{(2)})··· P(y^{(6)} = 1 | x^{(6)})
L(θ)=P(y(1)=0∣x(1))P(y(2)=0∣x(2))⋅⋅⋅P(y(6)=1∣x(6))
将联合概率一般化:
L
(
θ
)
=
∏
i
=
1
n
P
(
y
(
i
)
=
1
∣
x
(
i
)
)
y
(
i
)
P
(
y
(
i
)
=
0
∣
x
(
i
)
)
1
−
y
(
i
)
L(θ) =\prod_{i=1}^n P(y^{(i)} = 1 | x^{(i)})^{y^{(i)}} P(y^{(i)} = 0 | x^{(i)})^{1−y^{(i)}}
L(θ)=i=1∏nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)
回归的时候处理的是误差,所以要最小化,而现在考虑的是联合概率,我们希望概率尽可能大,所以要最大化。这里的目标函数
L
(
θ
)
L(\theta)
L(θ)也被称为似然,L就是Likelihood。
我们可以认为似然函数 L(θ) 中,使其值最大的参数 θ 能够最近似地说明训练数据。
1.对数似然函数
直接对似然函数进行微分有点困难,在此之前要把函数变形。取似然函数的对数,在等式两边加上 log:
log
L
(
θ
)
=
log
∏
i
=
1
n
P
(
y
(
i
)
=
1
∣
x
(
i
)
)
y
(
i
)
P
(
y
(
i
)
=
0
∣
x
(
i
)
)
1
−
y
(
i
)
\log L(θ) = \log \prod_{i=1}^n P(y^{(i)} = 1 | x^{(i)})^{y^{(i)}} P(y^{(i)} = 0 | x^{(i)})^{1−y^{(i)}}
logL(θ)=logi=1∏nP(y(i)=1∣x(i))y(i)P(y(i)=0∣x(i))1−y(i)
然后进行变形:
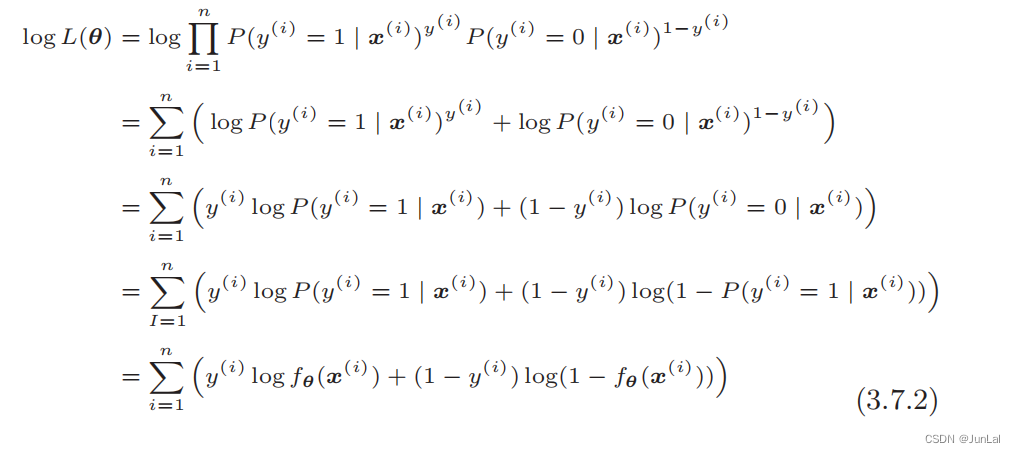
最终得到:
log
L
(
θ
)
=
∑
i
=
1
n
[
y
(
i
)
log
f
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
f
θ
(
x
(
i
)
)
)
]
\log L(θ) = \sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg]
logL(θ)=i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
2.似然函数的微分
逻辑回归就是要将这个对数似然函数用作目标函数:
log
L
(
θ
)
=
∑
i
=
1
n
[
y
(
i
)
log
f
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
f
θ
(
x
(
i
)
)
)
]
\log L(θ) = \sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg]
logL(θ)=i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
接下来对每个参数
θ
j
\theta_j
θj求微分:
∂
log
L
(
θ
)
∂
θ
j
=
∂
∂
θ
j
∑
i
=
1
n
[
y
(
i
)
log
f
θ
(
x
(
i
)
)
+
(
1
−
y
(
i
)
)
log
(
1
−
f
θ
(
x
(
i
)
)
)
]
\frac{\partial \log L(θ)}{\partial \theta_j} = \frac{\partial}{\partial \theta_j}\sum_{i=1}^n \bigg [y^{(i)}\log f_\theta(x^{(i)})+ (1−y^{(i)})\log (1 - f_\theta(x^{(i)})~)\bigg]
∂θj∂logL(θ)=∂θj∂i=1∑n[y(i)logfθ(x(i))+(1−y(i))log(1−fθ(x(i)) )]
接下来的求解步骤和回归的也差不多:
1.改写成复合函数求微分
u = log L ( θ ) v = f θ ( x ) ∂ u ∂ θ j = ∂ u ∂ v ⋅ ∂ v ∂ θ j u = \log L(\theta)\\ v = f_\theta(x)\\ \frac{\partial u}{\partial \theta_j} = \frac{\partial u}{\partial v} \cdot \frac{\partial v}{\partial \theta_j} u=logL(θ)v=fθ(x)∂θj∂u=∂v∂u⋅∂θj∂v
2.计算第一项 ∂ u ∂ v \frac{\partial u}{\partial v} ∂v∂u
∂ u ∂ v = ∂ ∂ θ j ∑ i = 1 n [ y ( i ) log ( v ) + ( 1 − y ( i ) ) log ( 1 − v ) ] d log ( v ) d v = 1 v , d log ( 1 − v ) d v = − 1 1 − v ∂ u ∂ v = ∑ i = 1 n ( y ( i ) v − 1 − y ( i ) 1 − v ) \frac{\partial u}{\partial v} = \frac{\partial}{\partial \theta_j}\sum_{i=1}^n \bigg [y^{(i)}\log(v)+ (1−y^{(i)})\log (1 - v)\bigg]\\ \frac{d\log(v)}{dv} = \frac{1}{v} , ~~\frac{d\log(1-v)}{dv} = -\frac{1}{1-v}\\ \frac{\partial u}{\partial v} = \sum_{i=1}^n(\frac{y^{(i)}}{v} - \frac{1−y^{(i)}}{1-v}) ∂v∂u=∂θj∂i=1∑n[y(i)log(v)+(1−y(i))log(1−v)]dvdlog(v)=v1, dvdlog(1−v)=−1−v1∂v∂u=i=1∑n(vy(i)−1−v1−y(i))
3.计算第二项 ∂ v ∂ θ j \frac{\partial v}{\partial \theta_j} ∂θj∂v
∂ v ∂ θ j = ∂ ∂ θ j 1 1 + e − θ T x z = θ T x v = f θ ( x ) = 1 1 + e − z ∂ v ∂ θ j = ∂ v ∂ z ⋅ ∂ z ∂ θ j \frac{\partial v}{\partial \theta_j }= \frac{\partial }{\partial \theta_j }\frac{1}{1+e^{-\theta^Tx}}\\ z = θ^Tx\\ v = f_θ(x) = \frac{1}{1 + e^{−z}}\\ \frac{\partial v}{\partial \theta_j} = \frac{\partial v}{\partial z} \cdot \frac{\partial z}{\partial \theta_j} ∂θj∂v=∂θj∂1+e−θTx1z=θTxv=fθ(x)=1+e−z1∂θj∂v=∂z∂v⋅∂θj∂z
其中(过程可以手推一次):
∂
v
∂
z
=
v
(
1
−
v
)
∂
z
∂
θ
j
=
x
j
\frac{\partial v}{\partial z} = v(1-v)\\ \frac{\partial z}{\partial \theta_j} = x_j\\
∂z∂v=v(1−v)∂θj∂z=xj
所以:
∂
v
∂
θ
j
=
v
(
1
−
v
)
⋅
x
j
\frac{\partial v}{\partial \theta_j} =v(1-v)\cdot x_j
∂θj∂v=v(1−v)⋅xj
4.整合
∂ u ∂ θ j = ∂ u ∂ v ⋅ ∂ v ∂ θ j = ∑ i = 1 n ( y ( i ) v − 1 − y ( i ) 1 − v ) ⋅ v ( 1 − v ) ⋅ x j ( i ) = ∑ i = 1 n ( y ( i ) ( 1 − v ) − ( 1 − y ( i ) ) v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − y ( i ) v − v + y ( i ) v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − v ) x j ( i ) = ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) ) x j ( i ) \begin{aligned} \frac{\partial u}{\partial \theta_j} &= \frac{\partial u}{\partial v} \cdot \frac{\partial v}{\partial \theta_j} \\ &=\sum_{i=1}^n(\frac{y^{(i)}}{v} - \frac{1−y^{(i)}}{1-v})\cdot v(1-v)\cdot x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)}(1-v) - (1−y^{(i)})v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - y^{(i)}v - v + y^{(i)}v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - v\bigg) x_j^{(i)}\\ &=\sum_{i=1}^n\bigg(y^{(i)} - f_θ(x^{(i)})\bigg) x_j^{(i)}\\ \end{aligned} ∂θj∂u=∂v∂u⋅∂θj∂v=i=1∑n(vy(i)−1−v1−y(i))⋅v(1−v)⋅xj(i)=i=1∑n(y(i)(1−v)−(1−y(i))v)xj(i)=i=1∑n(y(i)−y(i)v−v+y(i)v)xj(i)=i=1∑n(y(i)−v)xj(i)=i=1∑n(y(i)−fθ(x(i)))xj(i)
3.得到参数更新表达式
现在是以最大化为目标,所以必须按照与最小化时相反的方向移动参数,所以更新表达式中变成了+:
θ
j
:
=
θ
j
+
η
∑
i
=
1
n
(
y
(
i
)
−
f
θ
(
x
(
i
)
)
)
x
j
(
i
)
\theta_j := \theta_j + \eta\sum_{i=1}^n\bigg(y^{(i)} - f_θ(x^{(i)})\bigg) x_j^{(i)}
θj:=θj+ηi=1∑n(y(i)−fθ(x(i)))xj(i)
当然也可以为了和回归的式子保持一致,这样的话
η
\eta
η后面括号里面的式子就要变号了:
θ
j
:
=
θ
j
−
η
∑
i
=
1
n
(
f
θ
(
x
(
i
)
−
y
(
i
)
)
)
x
j
(
i
)
\theta_j := \theta_j - \eta\sum_{i=1}^n\bigg(f_θ(x^{(i)} - y^{(i)})\bigg) x_j^{(i)}
θj:=θj−ηi=1∑n(fθ(x(i)−y(i)))xj(i)
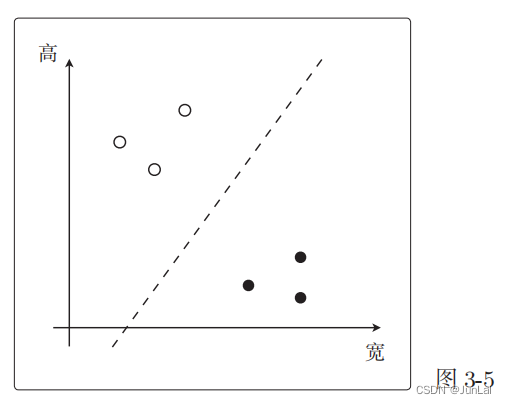
5.线性不可分
类似下图这样的,就是线性不可分:
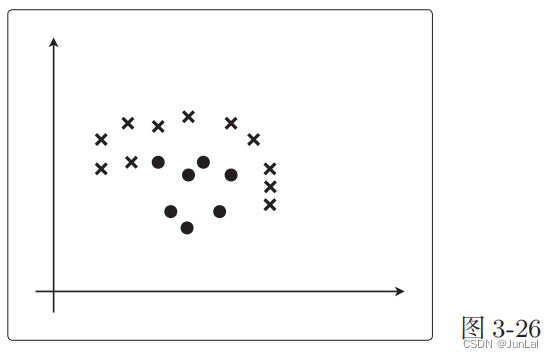
直线不能分类,但曲线是可以将其分类的。所以我们可以像学习多项式回归那样去增加次数。即:
θ
=
[
θ
0
θ
1
θ
2
θ
3
]
,
x
=
[
1
x
1
x
2
x
1
2
]
(2)
\theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \theta_3\\ \end{bmatrix} \tag{2} , x = \begin{bmatrix} 1\\x_1\\x_2\\x_1^2 \end{bmatrix}
θ=
θ0θ1θ2θ3
,x=
1x1x2x12
(2)
所以:
θ
T
x
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
\theta^Tx = \theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1^2
θTx=θ0+θ1x1+θ2x2+θ3x12
举个例子:
θ
=
[
θ
0
θ
1
θ
2
θ
3
]
=
[
0
0
1
−
1
]
(2)
\theta = \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ \theta_3\\ \end{bmatrix} \tag{2} = \begin{bmatrix} 0\\ 0\\ 1\\ -1\\ \end{bmatrix}
θ=
θ0θ1θ2θ3
=
001−1
(2)
所以:
θ
T
x
=
x
2
−
x
1
2
≥
0
\theta^Tx = x_2 - x_1^2 \ge 0
θTx=x2−x12≥0
对应的图像:

根据图像我们也可以看出。前面的决策边界是直线,现在是曲线。这也就是逻辑回归应用于线性不可分问题的方法。
通过随意地增加次数,就可以得到复杂形状的决策边界。
同样,在逻辑回归的参数更新中也可以使用随机梯度下降法。






![[C#]winform部署官方yolov8-rtdetr目标检测的onnx模型](https://img-blog.csdnimg.cn/direct/e9b3b70cde23419380fc19622de9105b.jpeg)