目录
前言:EXCEL里的的向量相关计算公式
0.1 EXCEL里相关公式
0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样
1 向量的点乘 (内积)
1.1 向量的点乘公式
1.2 EXCEL里向量点乘的计算
编辑
1.3 向量点乘的性质
1.3.1 内积的公式A*B=|A|*|B|*cos(θ)
1.3.1.2 cos曲线
1.3.2 内积的最大最小值
1.3.3 内积为正负的判断和应用---可用在机器学习上
1.3.4 内积的公式可以理解为
1.4 向量点乘=0时
2 向量组/矩阵的点乘
2.1 向量组/矩阵的点乘
2.2 EXCEL里向量组的乘法
2.3 公式
2.4 图
前言:EXCEL里的的向量相关计算公式
0.1 EXCEL里相关公式
- 向量组相乘 : mmult()
- 向量组转置 : transpose()
- 向量组取逆 : minverse()
0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样
- 向量的点乘 (内积), 可以用sumproduct(),也可以用mmult()
- 向量组的点乘 (内积),尽量用sumproduct(),也可以用 sum( mmult() ),但不能直接用 mmult()
1 向量的点乘 (内积)
1.1 向量的点乘公式
- 向量,这里是至一维向量
- 两个向量的点乘=行向量*列向量 = 常数/标量
- 内积=常数/标量
1.2 EXCEL里向量点乘的计算
- 两个向量的内积=行向量*列向量
- 如果行列向量,设置不对,计算时记得用 transpose()
- 所有矩阵的相乘都可以用muult()
- 但计算内积要注意有时候,只能用sumproduct()
1.3 向量点乘的性质
1.3.1 内积的公式A*B=|A|*|B|*cos(θ)
- 向量的内积=W*X=WT*X=|W|*|X|*cos(θ)
1.3.2 EXCEL里cos(θ) 的计算
- EXCEL里cos(θ) ,其中θ 必须是弧度
- 弧度=角度*PI()/180
- 弧度=RADIANS(角度)
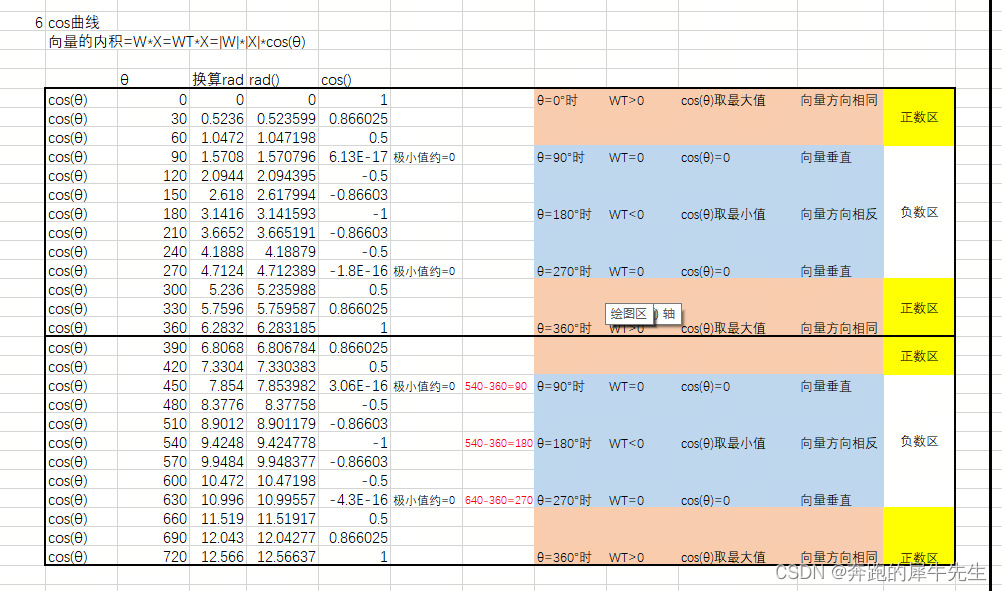
1.3.3 cos曲线
- 向量的内积=W*X=WT*X=|W|*|X|*cos(θ)
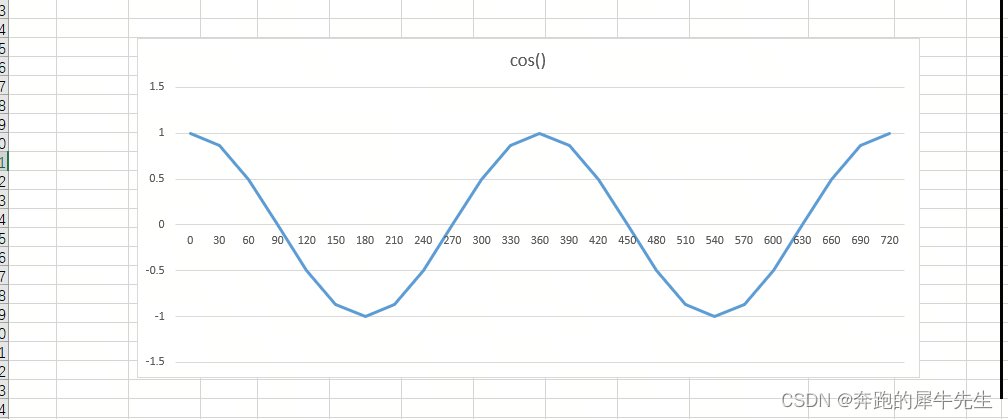
1.3.4 内积的最大最小值
最大值
- A*B=|A|*|B|*cos(θ)
- 当其他条件|A| |B| 的模长不变时,
- θ=0°,cos(θ)=1,
- 向量平行/共线,内积最大
- 向量内积最大
最小值
- θ=180°,cos(θ)=-1
- 向量方向相反,内积最小,为负数
1.3.5 内积为正负的判断和应用---可用在机器学习上
- 内积为负
- θ=90-270°之间时,cos(θ)<0,
- 内积为正
- θ=270-(360+90°)之间时,cos(θ)>0,
1.3.6 内积的公式可以理解为
- A*B=|A|*|B|*cos(θ)
- A*B=|A|*(|B|*cos(θ))
- A*B=|B|*(|A|*cos(θ))
内积=一个向量投影到另外一个向量上的分量
*另外一个向量
因此2个向量垂直90°时
向量的分量投影=0,因此内积=0
1.4 向量点乘=0时
- 两个向量内积为0 ,必然两个向量垂直/正交
- θ=90°,cos(θ)=0
- 因此垂直,正交时 A*B=0
- θ=90°,cos(θ)=0
- 向量正交垂直,内积并是最小
- 因为内积可以为负数

2 向量组/矩阵的点乘
2.1 向量组/矩阵的点乘
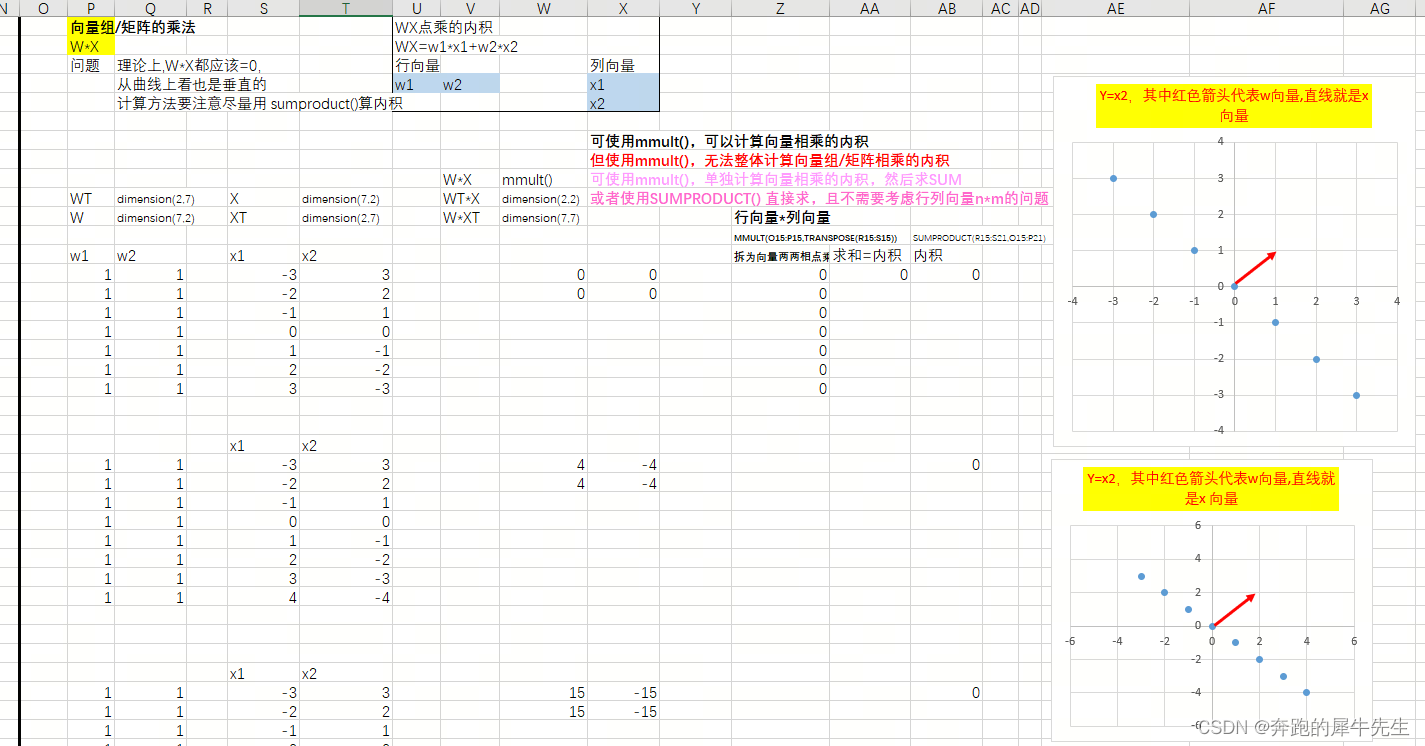
2.2 EXCEL里向量组的乘法
可使用mmult(),可以计算向量相乘的内积
但使用mmult(),无法整体计算向量组/矩阵相乘的内积
可使用mmult(),单独计算向量相乘的内积,然后求SUM
或者使用SUMPRODUCT() 直接求,且不需要考虑行列向量n*m的问题
2.3 公式

2.4 图










![[C#]winform部署官方yolov8-rtdetr目标检测的onnx模型](https://img-blog.csdnimg.cn/direct/e9b3b70cde23419380fc19622de9105b.jpeg)