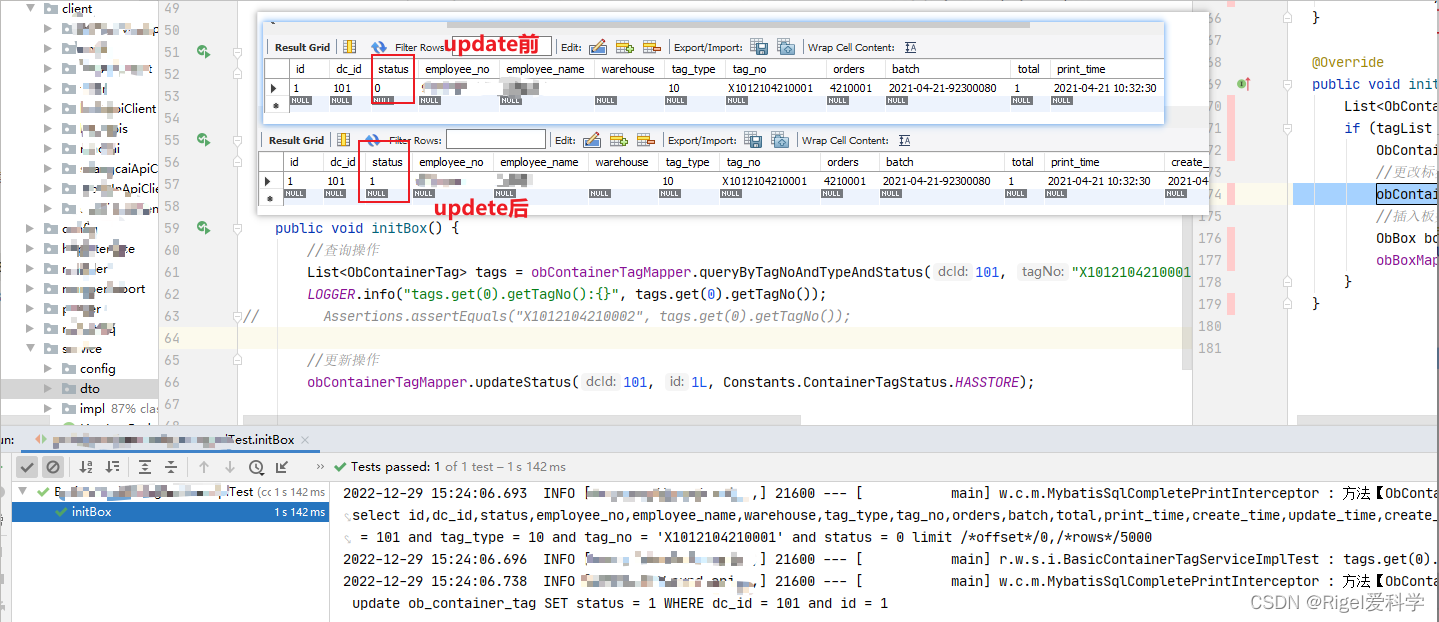
[NOIP2003 普及组] 栈

题目背景

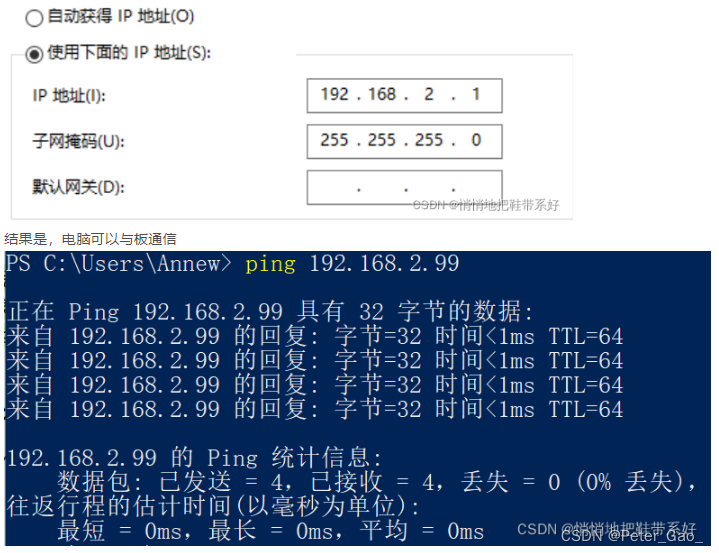
栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即 pop（从栈顶弹出一个元素）和 push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙。

题目描述

宁宁考虑的是这样一个问题：一个操作数序列，$1,2,\dots ,n$（图示为 1 到 3 的情况），栈 A 的深度大于 $n$。

现在可以进行两种操作，

1. 将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的 push 操作）
2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的 pop 操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由 1 2 3 生成序列 2 3 1 的过程。

（原始状态如上图所示）

你的程序将对给定的 $n$，计算并输出由操作数序列 $1,2,\dots ,n$ 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 $n$（$1\le n\le 18$）。

输出格式

输出文件只有一行，即可能输出序列的总数目。

样例 #1

样例输入 #1

3

样例输出 #1

5

提示

【题目来源】

NOIP 2003 普及组第三题

方法一：动态规划DP

1、思路

这道题一眼给我们的感觉就是方案数太多了，而且利用暴力DFS是可以解决的，但是效率太慢。此时我们就应该思考一下DP了。

（1）状态表示

$f(i,j)$表示的是，队列中的有$i$个元素，栈中有$j$个元素的时候，能够输出的栈序列总数。

（2）状态转移

一般情况下，我们面临的只有两种方式：

要么让队列中的元素入栈:$f(i-1,j+1)$

要么就是让队列中的元素不动，栈中的元素出队。
所以方程是：$f(i,j-1)$

$$f(i,j)=\{\begin{array}{ll}f(i-1,j+1)+f(i,j-1)& j\ge 1\\ f(i,j-1)& 0\le j<1\end{array}$$

（3）循环设计

循环的设计是为了保证每次利用状态转移方程求解问题的时候，方程右侧的子问题已经在此之前正确的求解。

如果说的高端一些，就是我们的循环设计要满足拓扑排序。

我们看方程：
在算$f(i,j)$的时候，我们要知道的子问题答案有：

$f(i-1,j+1)$ 和 $f(i,j-1)$

所以我们的外循环枚举$i$，内循环枚举$j$。如果反过来的话，我们会发现，我们含$j+1$的那一项无法在此之前算出。

（4）初末状态

初始状态是为了初始化最小的子问题，末尾状态是为了表示我们的答案。

我们的初始状态即当栈中的元素是j个，队列中的元素是0个的时候，我们只能出栈。此时只有1种序列。

还有就是当我们的队列中的元素只有1个，我们的栈中元素的个数是0的时候，我们此时的序列也是只有一种。

我们的最终状态是，队列中的元素个数是n，栈中的元素个数是0。即f[n][0]

2、代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20;
int f[N][N];
int main()
{
    int n;
    cin>>n;
    f[1][0]=1;
    for(int i=0;i<=n;i++)
        f[0][i]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=n;j++)
        {
            if(j!=0)
                f[i][j]=f[i-1][j+1]+f[i][j-1];
            else
                f[i][j]=f[i-1][j+1];
        }
    }
    cout<<f[n][0]<<endl;
    return 0;
}

方法二：DFS+记忆数组——记忆化搜索

记忆化搜索其实可以将动规的循环做法改为了函数递归的做法。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20;
int f[N][N];
int n;
int dfs(int i,int j)
{
    if(f[i][j])return f[i][j];
    if(i==0) return 1;
    if(j==0&&i==1)return 1;
    
    if(j>=1)f[i][j]=dfs(i-1,j+1)+dfs(i,j-1);
    else f[i][j]=dfs(i-1,j+1);

    return f[i][j];
}
int main()
{
    int n;
    cin>>n;
    cout<<dfs(n,0)<<endl;
    return 0;
}

方法三：数论——卡特兰数

如果有的同学不知道什么是卡特兰数的话，建议读者先去看一下作者在算法专栏中对卡特兰数的讲解。
传送门：

算法专栏——组合数之卡特兰数详解

1、为什么能用卡特兰数

我们发现卡特兰数的使用场景有以下的特点：
（1）只有两种操作
（2）过程中，其中一种操作的次数要大于等于另外一种操作的操作次数。最终两者的操作次数相等。

当满足上述特点的时候，就可以使用卡特兰数。

而我们这道题就两个操作，一个是入栈，一个是出栈，出栈的前提是栈中有元素。所以出栈的次数不能超过入栈的次数。但是最终我们的栈中元素要全部出栈。

所以满足上面的两个要求。

因此，可以使用卡特兰数。

2、代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll c(int a,int b)
{
    ll res=1;
    for(int i=1,j=a;i<=b;i++,j--)
    {
        res*=j;
        res/=i;
    }
    return res;
}
int main()
{
    int n;
    cin>>n;
    cout<<c(2*n,n)-c(2*n,n-1)<<endl;
}