玻纤效应对skew的影响（一）

玻纤效应对skew的影响（二）

对内skew对32Gbps NRZ和64Gbps PAM-4的影响

这一篇中，玻纤效应造成的对内skew将会加入到32Gbps NRZ和64Gbps PAM-4 SerDes全链路分析中。PCIe 5.0代表32Gbps NRZ，PCIe 6.0代表64Gbps PAM-4.

对内skew对PCIe5.0链路的影响

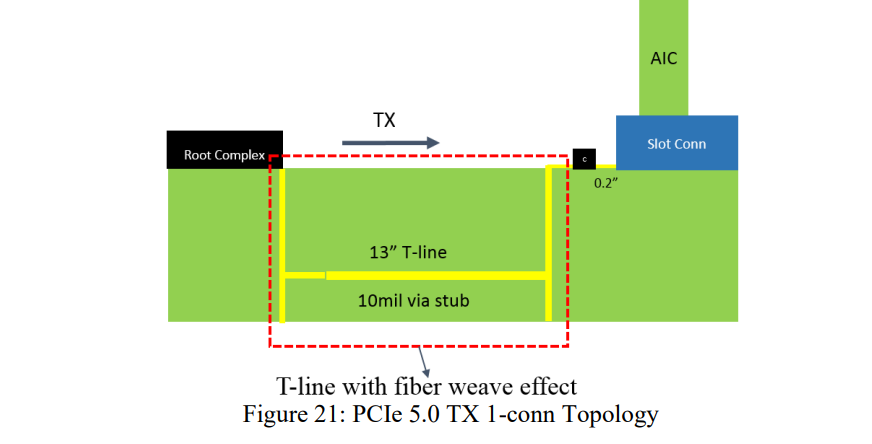
传输线模型会应用到PCIe5.0链路中，通过检查接收端眼图的大小判断玻纤效应的影响。要知道玻纤效应导致的对内skew是在传输线上一直持续的，并不是集中在某一点。下图是一个典型的一个连接器的PCIe5.0 Tx拓扑，使用2D模型构建的传输线模型中没有skew，我们以此为基准。ULL基板上传输线最长是13inch（参考Intel PDG），后面我们就会使用带玻纤效应的传输线模型替换理想传输线模型。

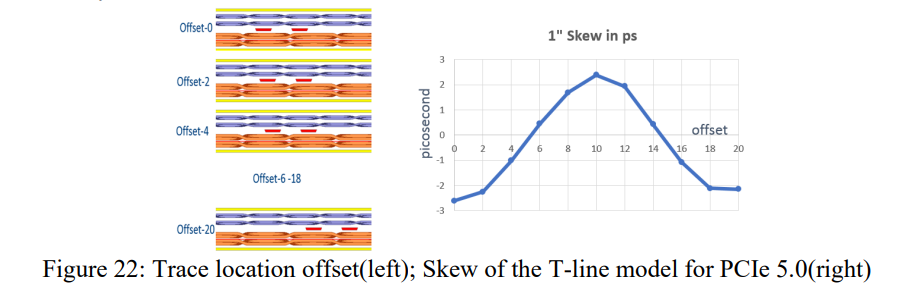
目前，扁平玻布已经广泛应用于高速系统中来消除玻纤效应，这些扁平布中玻璃束几乎没有空隙，玻璃束和玻璃束之间的开窗非常小。传输线模型也是基于扁平玻布来构建。skew会随着走线位置呈现周期性的变化，见下图。最大skew是2.6ps/inch，出现在0偏移的位置，最小的skew接近0ps/inch，出现在14偏移位置。

下图展示了眼高的变化趋势，和通道插损/对内skew展现了很强的关联性，而且，眼高和眼宽随着skew增加而减小，眼高表现更明显一些。

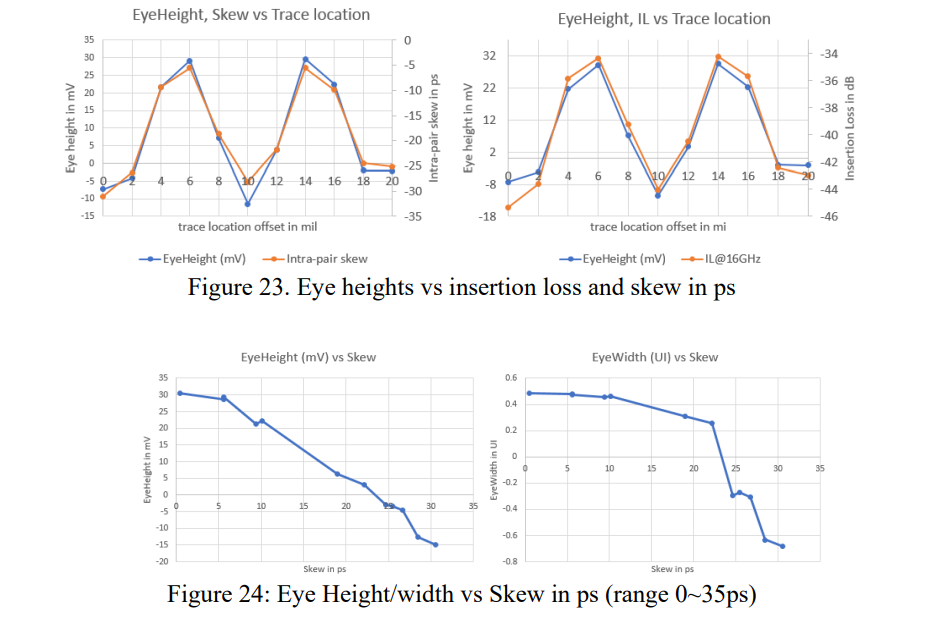
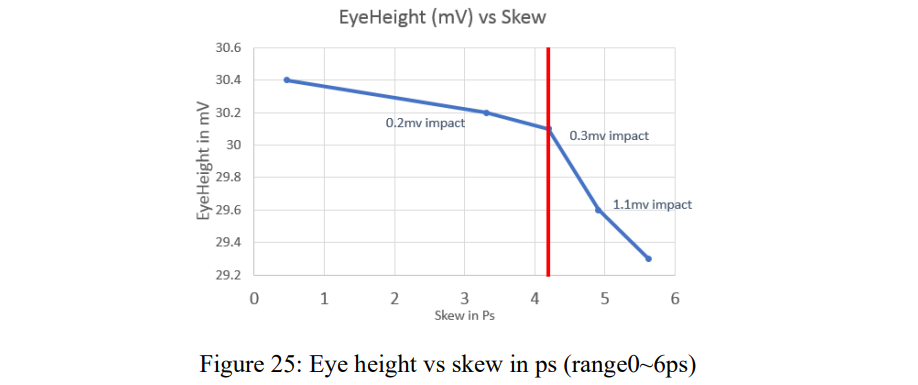
一些案例引入了超过 30 ps 的偏差，这显然超过了通道可以承受的范围。基于14偏移的模型（最小skew）新增加了一些case，这些case引发的skew从3ps到5ps。这里存在一个悬崖边界效应：如果对内skew在4.2ps内，眼图会随着skew增加缓慢缩小，一旦skew超过4.2ps，眼图会迅速变小，如下图所示。

当差分走线方向和玻璃束的经向或纬向方向平行时，就会出现对内skew，因此，就必须使这些平行的走线总长度最小。利用RSS长度来反映整体平行部分的重要性，计算公式如下图。

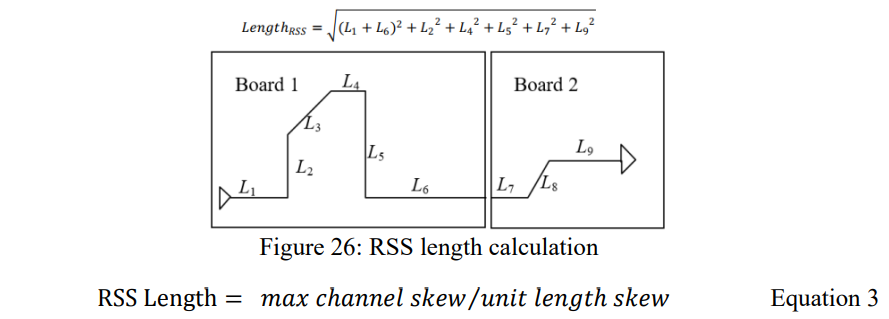
在上面的分析中，4.2ps是PCIe5.0链路中允许的最大对内skew。在上一篇文章的图19中，3.3ps/inch是推荐玻布规格中最大的skew，那么，4.2ps skew除以每英寸 3.3ps，根据公式 2 得出最大 1.2 英寸的 RSS 走线长度。Eagle Stream PDG [14] 中发布了最大 1.2 英寸 RSS 长度，用于指导 PCIe 5.0 应用的玻纤效应的缓解。

对内skew对PCIe6.0链路的影响

和PCIe5.0链路的分析类似，带玻纤效应的传输线模型应用于PCIe6.0拓扑的全链路分析中，下图是一个典型的一个连接器的PCIe6.0 Tx链路，所有的硅相关参数/终端模型都是基于PCIe6.0 base规范0.7版本。64Gbps PAM-4信号无法容忍和32Gbps NRZ一样大的skew，整个链路只能容忍8ps的skew。

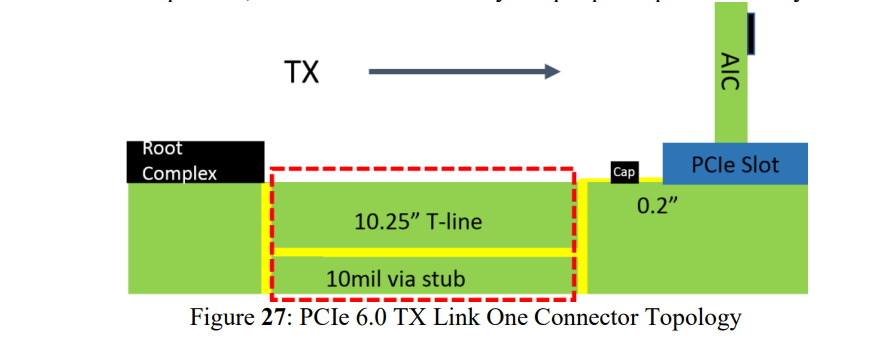
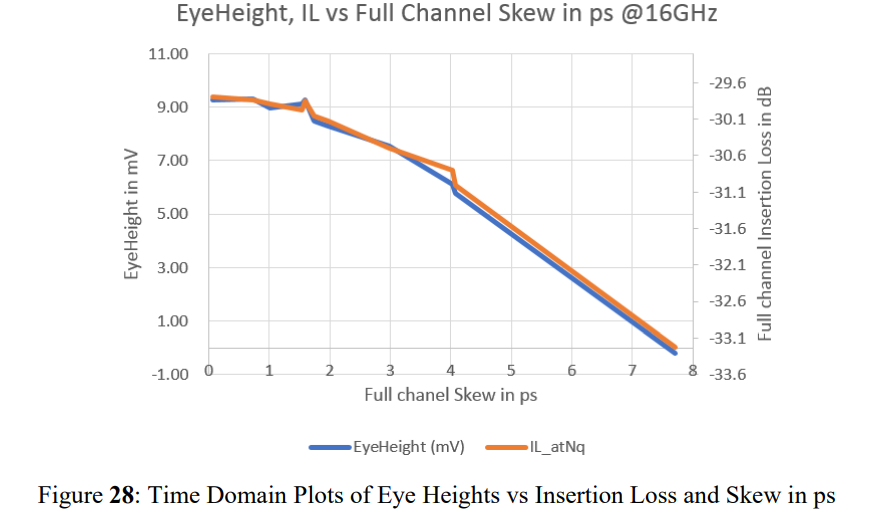
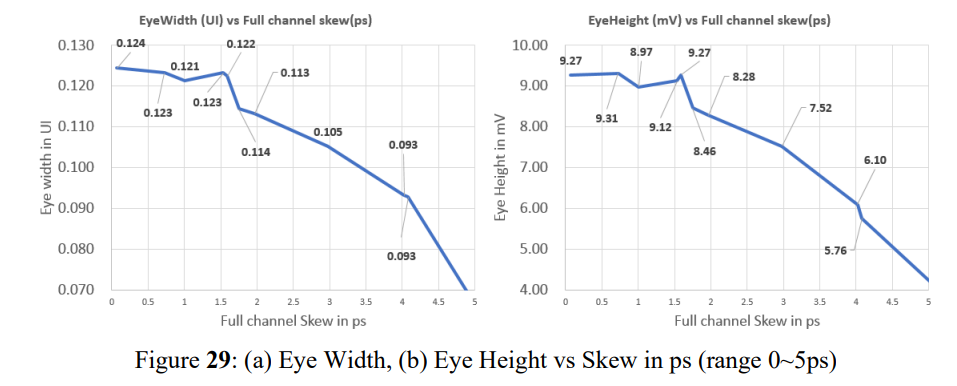
在上图中，这里只显示 PAM4 接收器眼图的底部眼高和宽度，因为顶部眼图对于线性系统是相同的，并且两者都比 PCIe 6.0 PAM-4 应用的中心眼图差。在该图中，随着skew增加，眼高劣化与插入损耗劣化几乎具有相同的趋势，这意味着对内skew导致插入损耗增加，眼高下降。眼高和眼宽下降与对内skew的关系如图 29 所示。鉴于 PCIe 6.0 的电压裕度相对较小（与 PCIE 5.0 相比），必须将对内skew对通道裕度的影响降至最低。在图 2829 中，当全通道偏移小于 1.6ps 时，对眼宽和眼高的影响可以忽略不计。建议最大 1.6ps 全通道对内偏移作为设计指南。

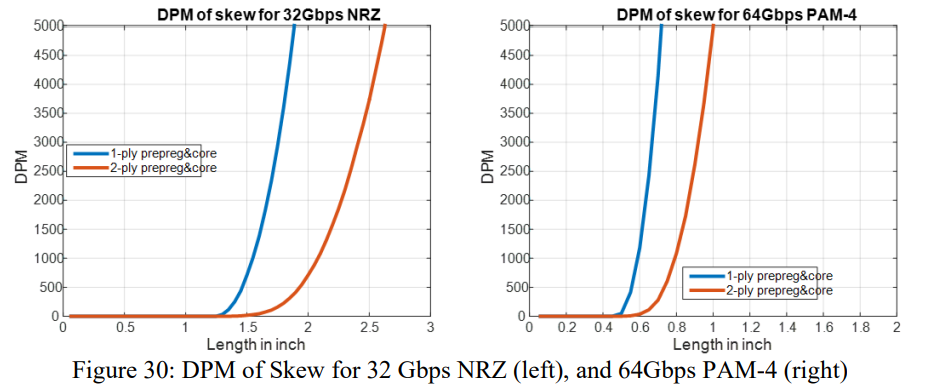
考虑到PCB上的skew是随机的，所以公式3有些过于悲观，合并经向和纬向的对内skew结果并进行统计学分析，为特定传输线布线长度（平行于电路板边缘）生成 100 万个案例，以检查有多少案例违反了上面提出的skew预算。上图显示，对于32Gbps NRZ，在DPM（defect per million）为50时，RSS长度可以达到1.3inch（使用单张core和pp）或者1.6inch（使用两张core和pp）。在DPM为5000时，长度可以继续增加至1.8inch和2.6inch。对于64Gbps PAM-4来说，当DPM为50时，相应的长度减小到0.5inch和0.6inch，当DPM为5000时，相应的长度增加到0.7inch和1inch。注意以上数据是基于4mil core 5mil PP的叠构，如果叠构有变化玻布规格也会有变化，RSS长度也会有变化。