近似算法
- 基本概念
- 可近似分类
- 最小顶点覆盖问题
- 近似算法的分析:
- 多机调度问题
- 近似算法贪心G-MPS
- 近似算法递降贪心法DG-MPS
- 货郎问题
- 最近邻NN算法
- 最小生成树法MST
- 最小权匹配MM算法
- 0-1背包问题
- 贪心G-KK
- 多项式近似方案
- 完全多项式时间的近似方案
- 背包问题的对偶问题
- 总结
基本概念
指标要求:
时间——多项式时间
性能——近似比为常数
近似算法适用于组合优化问题,一般是多项式时间的算法
近似算法有一个可行解和值
近似比 r:衡量近似算法A的误差有多大
例如:
算法A的近似比r
设OPT(I)表示实例I的最优解的值
(1)
∏
是最大化问题,
r
A
(
I
)
=
A
(
I
)
/
O
P
T
(
I
)
\prod{}{}是最大化问题,r_{A}(I)=A(I)/OPT(I)
∏是最大化问题,rA(I)=A(I)/OPT(I)
(2)
∏
是最大化问题,
r
A
(
I
)
=
O
P
T
(
I
)
/
A
(
I
)
\prod{}{}是最大化问题,r_{A}(I)=OPT(I)/A(I)
∏是最大化问题,rA(I)=OPT(I)/A(I)
r
A
(
I
)
>
=
1
r_{A}(I)>=1
rA(I)>=1
最优算法A:对所有的实例
I
I
I,恒有
A
(
I
)
=
O
P
T
(
I
)
即
r
A
(
I
)
=
1
A(I)=OPT(I)即r_{A}(I)=1
A(I)=OPT(I)即rA(I)=1
A的近似比为
r
r
r(A是
r
−
r-
r−近似算法)
A具有常数近似比:
r
r
r是一个常数
可近似分类
假设
P
≠
N
P
,
N
P
P\neq NP,NP
P=NP,NP难问题的组合优化问题按可近似性可分成三类
完全可近似的:对任意小的
ϵ
>
0
\epsilon>0
ϵ>0,存在
(
1
+
ϵ
)
−
(1+\epsilon)-
(1+ϵ)−近似算法,例如背包问题。(误差很小或者完全可近似)
可近似的:存在具有常数比的近似算法,例如最小顶点覆盖问题、多机调度问题。
不可近似的:不存在常数比的近似算法,例如货郎问题。(不可近似,但是一些子问题例如输入参数在某些限制条件下可以考虑可近似计算)
最小顶点覆盖问题


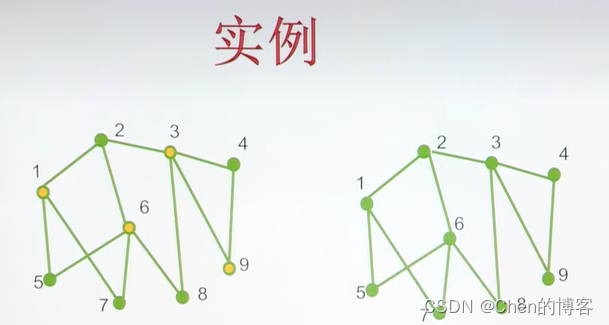
按照MVC算法来操作,依次取边1-2、2-3、3-4、5-6,最终可得到近似顶点覆盖{1,2,3,4,5,6}
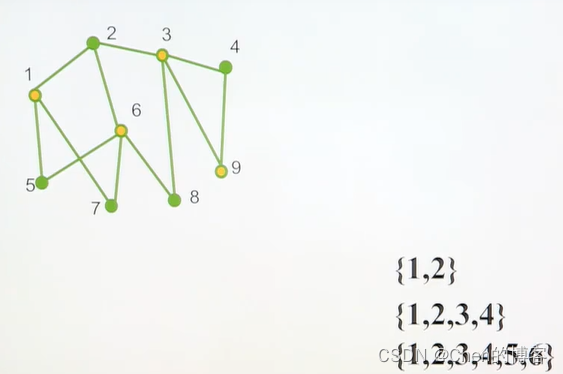
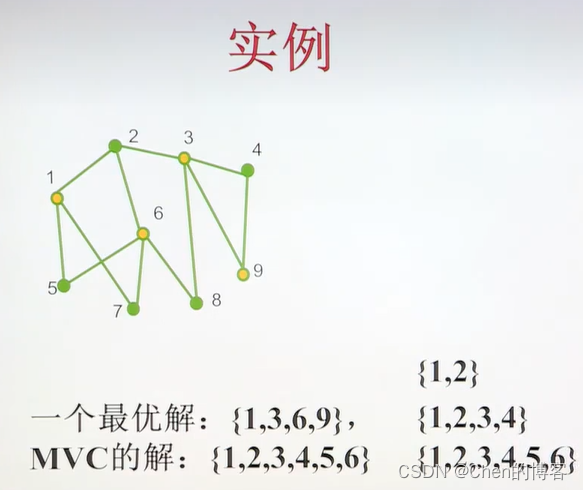
MVC算法分析

按照上述分析,可得MVC算法近似比为2,MVC近似算法可近似。
MVC也可有更好的近似比,如果我们能找到一个更好的数学证明方法得到更好的近似比,就能说明MVC算法近似比<2,得到更精确。
证明MVC算法近似比为2,可以找一个实例,得到MVC的覆盖顶点集/最优覆盖顶点集等于2或者几乎等于2,这时就能说明MVC算法近似比为2(上界为2)。
例如:


近似算法的分析:
运行时间:一般是多项式时间
近似比
(1)估计上界:建立最优值与近似解值之间的关系(
近似出
r
近似出r
近似出r)
(2)估计下界:构造使算法产生最坏解的实例,如果这个解的值与最优值的比(最小化问题,最大化相反比)达到或可以任意接近近似比的上界(称作紧实例),那么这个近似比已经是最好的。


多机调度问题

近似算法贪心G-MPS


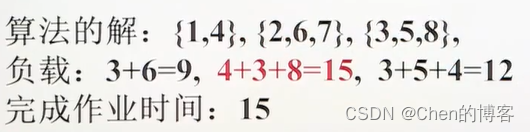







近似算法递降贪心法DG-MPS





货郎问题

最近邻NN算法





最小生成树法MST

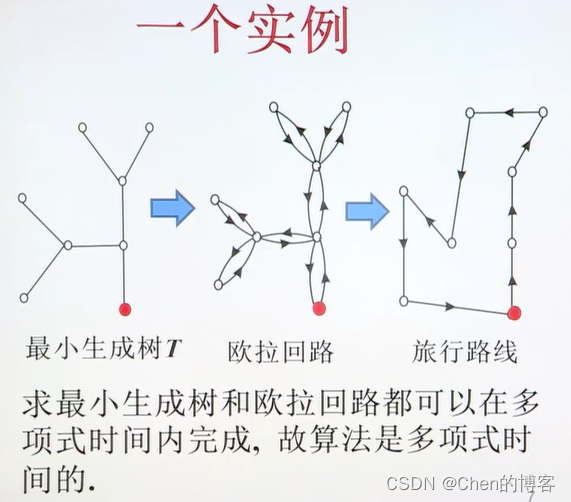


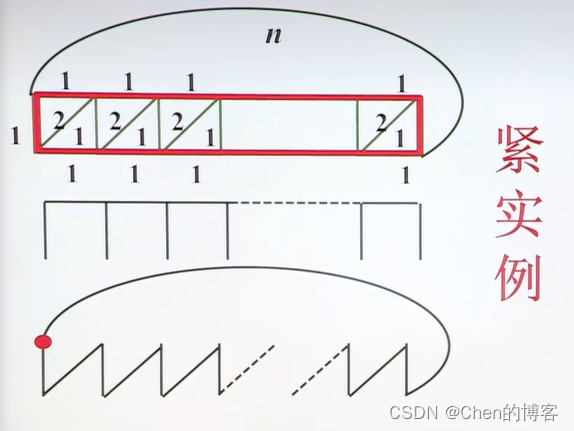
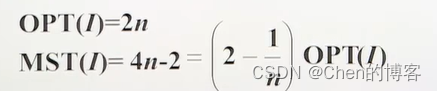
最小权匹配MM算法



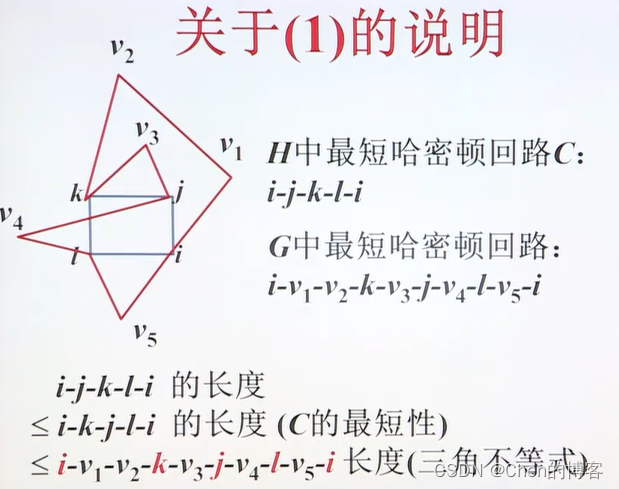







0-1背包问题

贪心G-KK



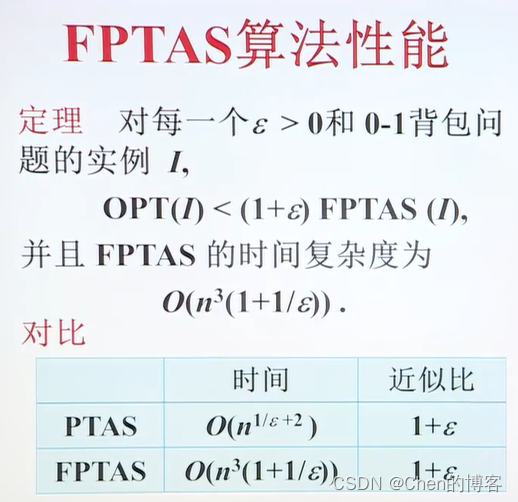
多项式近似方案


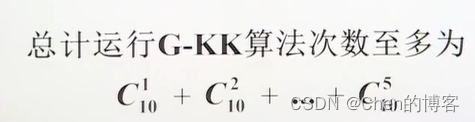







完全多项式时间的近似方案
背包问题的对偶问题

价值变为约束条件,价值>=V的条件下找最小重量


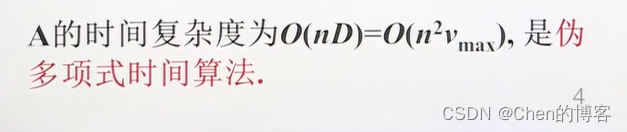




总结