every blog every motto: You can do more than you think.
0. 前言
遗传算法是一种基于自然选择和遗传机制的优化算法,因此它通常被用于求解各种最优化问题,例如函数优化、特征选择、图像处理等。
一言以蔽之: 将数学中的优化问题,首先通过“编码”将数字变成“0101”类似这种二进制形式(不绝对),然后对其进行变换(“变异”),根据提前指定的“目标函数”(适应度)对这组数学进行筛选,重复这个过程一定次数(“迭代进化”),最终找到最优解

1. 简介
1.1 概念
遗传算法(Genetic Algorithm,简称GA)受自然进化理论启发的一系列搜索算法,起源于对生物系统所进行的计算机模拟研究,是一种随机全局搜索优化方法,它模拟了自然选择和遗传中发生的复制、交叉(crossover)和变异(mutation)等现象,从任一初始种群(Population)出发,通过随机选择、交叉和变异操作,产生一群更适合环境的个体,使群体进化到搜索空间中越来越好的区域,这样一代一代不断繁衍进化,最后收敛到一群最适应环境的个体(Individual),从而求得问题的优质解。
达尔文进化论原理概括为:
- 变异:种群中单个样本的特征(性状,属性)可能会有所不同,这导致了样本彼此之间有一定程度的差异。
- 遗传:某些特征可以遗传给其后代。导致后代与双亲样本具有一定程度的相似性。
- 选择:种群通常在给定的环境中争夺资源。更适应环境的个体在生存方面更具优势,因此会产生更多的后代。
1.2 术语
- 染色体(Chromosome): 染色体又可称为基因型个体(individuals),一定数量的个体组成了群体(population),群体中个体的数量叫做群体大小(population size)
- 位串(Bit String): 个体的表示形式。对应于遗传学中的染色体
- 基因(Gene): 基因是染色体中的元素,用于表示个体的特征。例如有一个串(即染色体)S=1011,则其中的1,0,1,1这4个元素分别称为基因
- 特征值( Feature): 在用串表示整数时,基因的特征值与二进制数的权一致;例如在串 S=1011 中,基因位置3中的1,它的基因特征值为2;基因位置1中的1,它的基因特征值为8
- 适应度(Fitness): 各个个体对环境的适应程度叫做适应度(fitness)。为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数。这个函数通常会被用来计算个体在群体中被使用的概率
- 基因型(Genotype): 或称遗传型,是指基因组定义遗传特征和表现。对于于GA中的位串
- 表现型(Phenotype): 生物体的基因型在特定环境下的表现特征。对应于GA中的位串解码后的参数

1.3 算法流程
1.3.1 整体流程
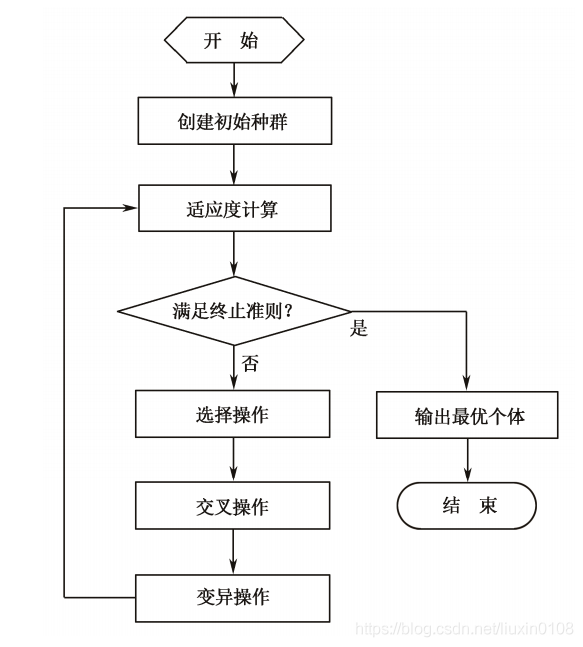
- 初始化。 设置进化代数计数器g=0,设置最大进化代数G,随机生成NP个个体作为初始群P(0)
- 个体评价。 计算群体P(t)中各个个体的适应度
- 选择运算。 将选择算子作用于群体,根据个体的适应度,按照一定的规则或方法,选择一些优良个体遗传到下一代群体
- 交叉运算。 将交叉算子作用于群体,对选中的成对个体,以某一概率交换他们的之间的染色体,产生新个体
- 变异运算。 将变异算子作用于群体,对选中的个体,以某一概率改变某一个或某一些基因值为其他的等位基因。群体P(t)经过选择、交叉和变异运算之后得到下一代群体P(t+1),计算适用值,并根据适应值进行排序,准备进行下一次遗传操作
- 终止条件判断。 若g<G,则g=g+1,转到步骤2,否则,进化过程中所得到的具有最大适应度的个体作为最优解输出,终止计算。
1.3.2 关键参数
- 群体规模
群体规模将影响遗传优化的最终结果以及遗传算法的执行效率。当群体规模 NP太小时,遗传优化性能一般不会太好。采用较大的群体规模可以减小遗传算法陷入局部最优解的机会,但较大的群体规模意味着计算复杂度较高。一般 NP 取 10~20010~200。
- 交叉概率
交叉概率 P c P_c Pc控制着交叉操作被使用的频度。较大的交叉概率可以增强遗传算法开辟新的搜索区域的能力,但高性能的模式遭到破坏的可能性增大;若交叉概率太低,遗传算法搜索可能陷入迟钝状态。一般 P c P_c Pc取 0.25~1.000.25~1.00。
- 变异概率
变异在遗传算法中属于辅助性的搜索操作,它的主要目的是保持群体的多样性。一般低频度的变异可防止群体中重要基因的可能丢失,高频度的变异将使遗传算法趋于纯粹的随机搜索。通常 P m P_m Pm取 0.001~0.10.001~0.1。
- 进化代数
终止进化代数 G是表示遗传算法运行结束条件的一个参数,它表示遗传算法运行到指定的进化代数之后就停止运行,并将当前群体中的最佳个体作为所求问题的最优解输出。一般视具体问题而定,G的取值可在 100~1000100~1000 之间。
1.3.3 关键步骤
1. 染色体编码
在计算中处理的数据,而对于具体的遗传算法 需要将常见的数据转换成“基因”,即0101这种形式,常见的编码方式有:
- 二进制编码: 即组成染色体的基因序列是由二进制数表示,具有编码解码简单易用,交叉变异易于程序实现等特点
- 格雷码编码: 两个相邻的数用格雷码表示,其对应的码位只有一个不相同,从而可以提高算法的局部搜索能力。这是格雷码相比二进制码而言所具备的优势。
- 浮点数编码: 是指将个体范围映射到对应浮点数区间范围,精度可以随浮点数区间大小而改变
- 各参数级联编码
- 多参数交叉编码
2. 解码
遗传算法染色体向问题解的转换
3. 适应度评估检测
适应度函数表明个体或解的优劣性。对于不同的问题,适应度函数的定义方式不同。根据具体问题,计算群体P(t)中各个个体的适应度。
适应度尺度变换: 一般来讲,是指算法迭代的不同阶段,能够通过适当改变个体的适应度大小,进而避免群体间适应度相当而造成的竞争减弱,导致种群收敛于局部最优解。包括:
- 线性尺度变换
- 乘幂尺度变换
- 指数尺度变换
4. 遗传算子
包括以下三种遗传算子:
- 选择: 选择操作从旧群体中以一定概率选择优良个体组成新的种群,以繁殖得到下一代个体。个体被选中的概率与适应度有关,具体可以使用轮盘赌法
- 交叉: 交叉操作是指从种群中随机选择两个个体,通过两个染色体的交换组合,把父串的优秀特征遗传给子串,从而产生新的优秀个体。
- 变异: 为了防止遗传算法在优化过程中陷入局部最优解,在搜索过程中,需要对个体进行变异,在实际应用中,主要采用单点变异,也叫位变异,即只需要对基因序列中某一个位进行变异,以二进制编码为例,即0变为1,而1变为0。
5. 预先设定参数
- 种群大小:M
- 遗传算法终止进化代数:T
- 交叉概率: P c P_c Pc , 一般取0.4~0.99
- 变异概率, P m P_m Pm , 一般取0.001~0.1
1.4 应用
1.4.1 应用范围
- 旅行商问题(Traveling Salesman Problem):旅行商问题是一个经典的组合优化问题,目标是找到一条路径,使得旅行商能够访问所有城市并返回起始城市,同时总路线最短。遗传算法可以用来寻找近似最优解。
- 机器调度问题(Machine Scheduling Problem):机器调度问题涉及将若干任务分配给多台机器,并确定任务的执行顺序和时间,以最大化生产效率或最小化完成时间。遗传算法可以用来优化任务的分配和调度策略。
- 参数优化问题(Parameter Optimization):在许多科学和工程领域中,需要通过调整模型或算法中的参数来优化性能指标。遗传算法可以用来搜索参数空间,找到最优的参数组合,从而优化模型或算法的性能。
- 神经网络训练(Neural Network Training):神经网络的训练通常涉及调整网络的权重和偏置,以最小化损失函数。遗传算法可以用来搜索神经网络的参数空间,寻找最优的权重和偏置组合,从而提高网络的性能。
- 组合优化问题(Combinatorial Optimization):组合优化问题涉及在给定约束条件下,从大量组合中找到最优解。例如,图的着色问题、背包问题等。遗传算法可以用来搜索组合空间,找到满足约束条件并具有最优特性的组合。
1.4.2 应用案例
案例一:TSP问题
以下是一个简单的遗传算法的 Python 代码示例,用于解决旅行商问题(Traveling Salesman Problem)
import random
# 定义城市列表和距离矩阵
city_list = ['A', 'B', 'C', 'D', 'E']
distance_matrix = {
'A': {'A': 0, 'B': 2, 'C': 9, 'D': 10, 'E': 5},
'B': {'A': 1, 'B': 0, 'C': 6, 'D': 4, 'E': 8},
'C': {'A': 9, 'B': 6, 'C': 0, 'D': 3, 'E': 7},
'D': {'A': 10, 'B': 4, 'C': 3, 'D': 0, 'E': 6},
'E': {'A': 5, 'B': 8, 'C': 7, 'D': 6, 'E': 0}
}
# 遗传算法参数设置
population_size = 50
elite_size = 10
mutation_rate = 0.01
generations = 100
# 创建一个随机个体(路径)
def create_individual(city_list):
individual = random.sample(city_list, len(city_list))
return individual
# 创建初始种群
def create_population(city_list, population_size):
population = []
for _ in range(population_size):
individual = create_individual(city_list)
population.append(individual)
return population
# 计算路径的总距离
def calculate_fitness(individual):
total_distance = 0
for i in range(len(individual)-1):
city1 = individual[i]
city2 = individual[i+1]
total_distance += distance_matrix[city1][city2]
return total_distance
# 选择精英个体
def select_elite(population, elite_size):
population_fitness = [(individual, calculate_fitness(individual)) for individual in population]
population_fitness = sorted(population_fitness, key=lambda x: x[1])
elite = [individual for individual, _ in population_fitness[:elite_size]]
return elite
# 进行交叉操作
def crossover(parent1, parent2):
child = [None] * len(parent1)
geneA = random.randint(0, len(parent1)-1)
geneB = random.randint(0, len(parent1)-1)
start_gene = min(geneA, geneB)
end_gene = max(geneA, geneB)
for i in range(start_gene, end_gene+1):
child[i] = parent1[i]
for i in range(len(parent2)):
if parent2[i] not in child:
for j in range(len(child)):
if child[j] is None:
child[j] = parent2[i]
break
return child
# 进行变异操作
def mutate(individual):
for i in range(len(individual)):
if random.random() < mutation_rate:
j = random.randint(0, len(individual)-1)
individual[i], individual[j] = individual[j], individual[i]
return individual
# 进化函数
def evolve_population(population, elite_size):
elite = select_elite(population, elite_size)
population_size = len(population)
children = []
while len(children) < population_size:
parent1 = random.choice(elite)
parent2 = random.choice(elite)
child = crossover(parent1, parent2)
child = mutate(child)
children.append(child)
return children
# 主函数
def main():
population = create_population(city_list, population_size)
for i in range(generations):
population = evolve_population(population, elite_size)
best_individual = min(population, key=calculate_fitness)
best_distance = calculate_fitness(best_individual)
print("最佳路径:", best_individual)
print("最短距离:", best_distance)
if __name__ == '__main__':
main()
案例二:极值问题
以下是求 f = x 2 f=x^2 f=x2的极值问题,设自变量x介于0~31之间,求二次函数的最大值
步骤:
(1)编码 遗传算法首先要对实际问题进行编码,用字符串表达问题。这种字符串相当于遗传学中的染色体。每一代所产生的字符串个体总和称为群体。为了实现的方便,通常字符串长度固定,字符选0或1。 本例中,利用5位二进制数表示x值,采用随机产生的方法,假设得出拥有四个个体的初始群体,即:01101,11000,01000,10011。x值相应为13,24,8,19。

(2)计算适应度 衡量字符串(染色体)好坏的指标是适应度,它也就是遗传算法的目标函数。本例中用 x 2 x^2 x2计算。

(3)复制 根据相对适应度的大小对个体进行取舍,2号个体性能最优,予以复制繁殖。3号个体性能最差,将它删除,使之死亡,表中的M表示传递给下一代的个体数目,其中2号个体占2个,3号个体为0,1号、4号个体保持为1个。这样,就产生了下一代群体

复制后产生的新一代群体的平均适应度明显增加,由原来的293增加到421 (4)交换 利用随机配对的方法,决定1号和2号个体、3号和4号个体分别交换,如表中第5列。再利用随机定位的方法,确定这两对母体交叉换位的位置分别从字符长度的第4位及第3位开始。如:3号、4号个体从字符长度第3位开始交换。交换开始的位置称交换点

(5)突变 将个体字符串某位符号进行逆变,即由1变为0或由0变为1。例如,下式左侧的个体于第3位突变,得到新个体如右侧所示。

遗传算法中,个体是否进行突变以及在哪个部位突变,都由事先给定的概率决定。通常,突变概率很小,本例的第一代中就没有发生突变。
上述(2)~(5)反复执行,直至得出满意的最优解。
综上可以看出,遗传算法参考生物中有关进化与遗传的过程,利用复制、交换、突变等操作,不断循环执行,逐渐逼近全局最优解。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
DNA_SIZE = 24
POP_SIZE = 80
CROSSOVER_RATE = 0.6
MUTATION_RATE = 0.01
N_GENERATIONS = 100
X_BOUND = [-2.048, 2.048]
Y_BOUND = [-2.048, 2.048]
def F(x, y):
return 100.0 * (y - x ** 2.0) ** 2.0 + (1 - x) ** 2.0 # 以香蕉函数为例
def plot_3d(ax):
X = np.linspace(*X_BOUND, 100)
Y = np.linspace(*Y_BOUND, 100)
X, Y = np.meshgrid(X, Y)
Z = F(X, Y)
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
plt.pause(3)
plt.show()
def get_fitness(pop):
x, y = translateDNA(pop)
pred = F(x, y)
return pred
# return pred - np.min(pred)+1e-3 # 求最大值时的适应度
# return np.max(pred) - pred + 1e-3 # 求最小值时的适应度,通过这一步fitness的范围为[0, np.max(pred)-np.min(pred)]
def translateDNA(pop): # pop表示种群矩阵,一行表示一个二进制编码表示的DNA,矩阵的行数为种群数目
x_pop = pop[:, 0:DNA_SIZE] # 前DNA_SIZE位表示X
y_pop = pop[:, DNA_SIZE:] # 后DNA_SIZE位表示Y
x = x_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (X_BOUND[1] - X_BOUND[0]) + X_BOUND[0]
y = y_pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2 ** DNA_SIZE - 1) * (Y_BOUND[1] - Y_BOUND[0]) + Y_BOUND[0]
return x, y
def crossover_and_mutation(pop, CROSSOVER_RATE=0.8):
new_pop = []
for father in pop: # 遍历种群中的每一个个体,将该个体作为父亲
child = father # 孩子先得到父亲的全部基因(这里我把一串二进制串的那些0,1称为基因)
if np.random.rand() < CROSSOVER_RATE: # 产生子代时不是必然发生交叉,而是以一定的概率发生交叉
mother = pop[np.random.randint(POP_SIZE)] # 再种群中选择另一个个体,并将该个体作为母亲
cross_points = np.random.randint(low=0, high=DNA_SIZE * 2) # 随机产生交叉的点
child[cross_points:] = mother[cross_points:] # 孩子得到位于交叉点后的母亲的基因
mutation(child) # 每个后代有一定的机率发生变异
new_pop.append(child)
return new_pop
def mutation(child, MUTATION_RATE=0.003):
if np.random.rand() < MUTATION_RATE: # 以MUTATION_RATE的概率进行变异
mutate_point = np.random.randint(0, DNA_SIZE) # 随机产生一个实数,代表要变异基因的位置
child[mutate_point] = child[mutate_point] ^ 1 # 将变异点的二进制为反转
def select(pop, fitness): # nature selection wrt pop's fitness
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,
p=(fitness) / (fitness.sum()))
return pop[idx]
def print_info(pop):
fitness = get_fitness(pop)
max_fitness_index = np.argmax(fitness)
print("max_fitness:", fitness[max_fitness_index])
x, y = translateDNA(pop)
print("最优的基因型:", pop[max_fitness_index])
print("(x, y):", (x[max_fitness_index], y[max_fitness_index]))
print(F(x[max_fitness_index], y[max_fitness_index]))
if __name__ == "__main__":
fig = plt.figure()
# ax = Axes3D(fig)
ax = fig.add_axes(Axes3D(fig))
plt.ion() # 将画图模式改为交互模式,程序遇到plt.show不会暂停,而是继续执行
plot_3d(ax)
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE * 2)) # matrix (POP_SIZE, DNA_SIZE)
for _ in range(N_GENERATIONS): # 迭代N代
x, y = translateDNA(pop)
if 'sca' in locals():
sca.remove()
sca = ax.scatter(x, y, F(x, y), c='black', marker='o')
plt.show()
plt.pause(0.1)
pop = np.array(crossover_and_mutation(pop, CROSSOVER_RATE))
fitness = get_fitness(pop)
pop = select(pop, fitness) # 选择生成新的种群
print_info(pop)
plt.ioff()
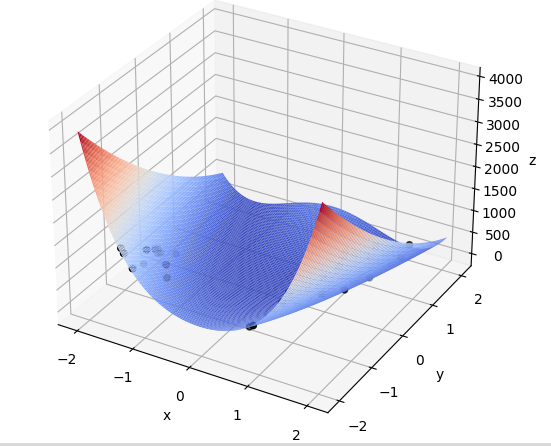
plot_3d(ax)
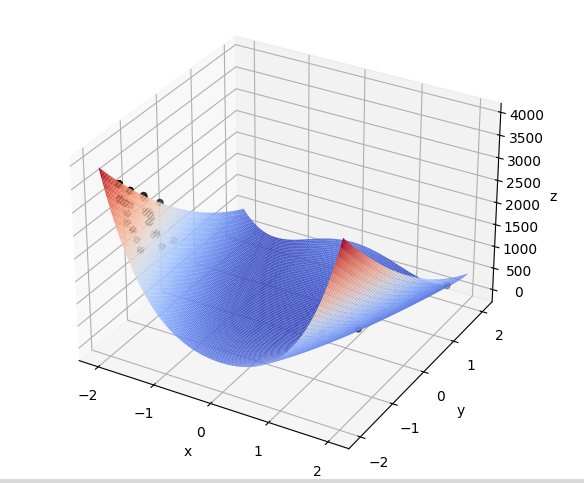
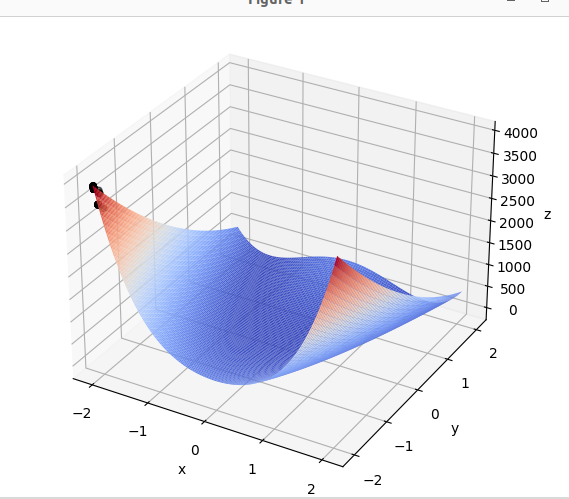
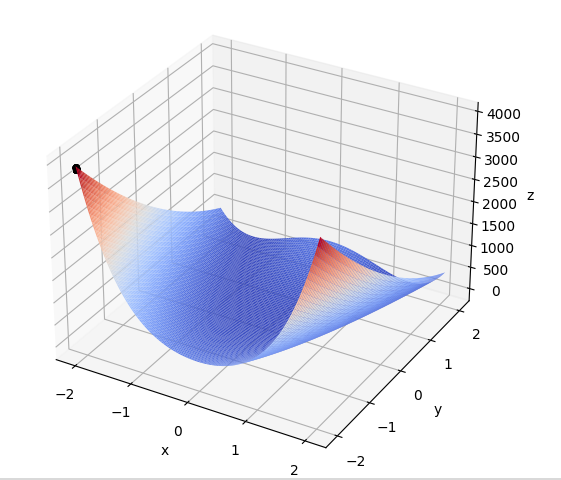
具体过程是一个动图,如下仅截几张作为示例:
参考
[1] https://zhuanlan.zhihu.com/p/378906456
[2] https://blog.csdn.net/liuxin0108/article/details/115923169
[3] https://zhuanlan.zhihu.com/p/100337680