前言
- 📚 笔记专栏:斯坦福CS231N:面向视觉识别的卷积神经网络(23)
- 🔗 课程链接:https://www.bilibili.com/video/BV1xV411R7i5
- 💻 CS231n: 深度学习计算机视觉(2017)中文笔记:https://zhuxiaoxia.blog.csdn.net/article/details/80155166
- 🔥 2023最新课程PPT:https://download.csdn.net/download/Julialove102123/88734395
⚠️ 本节重点内容:
- 正则化Regularization
- 最优化Optimization
- 梯度下降 Grendient descent
- 学习率Learning rate
1. 正则化(Regularization)
1.1 为什么引入正则化
上节讲到了如何选择最合适的超参数W,那有没有可能会出现多个这样的参数W1、W2…都能似的损失函数最小呢,答案是非常有可能!!!本节引入正则化就是确定怎么选最合适的W。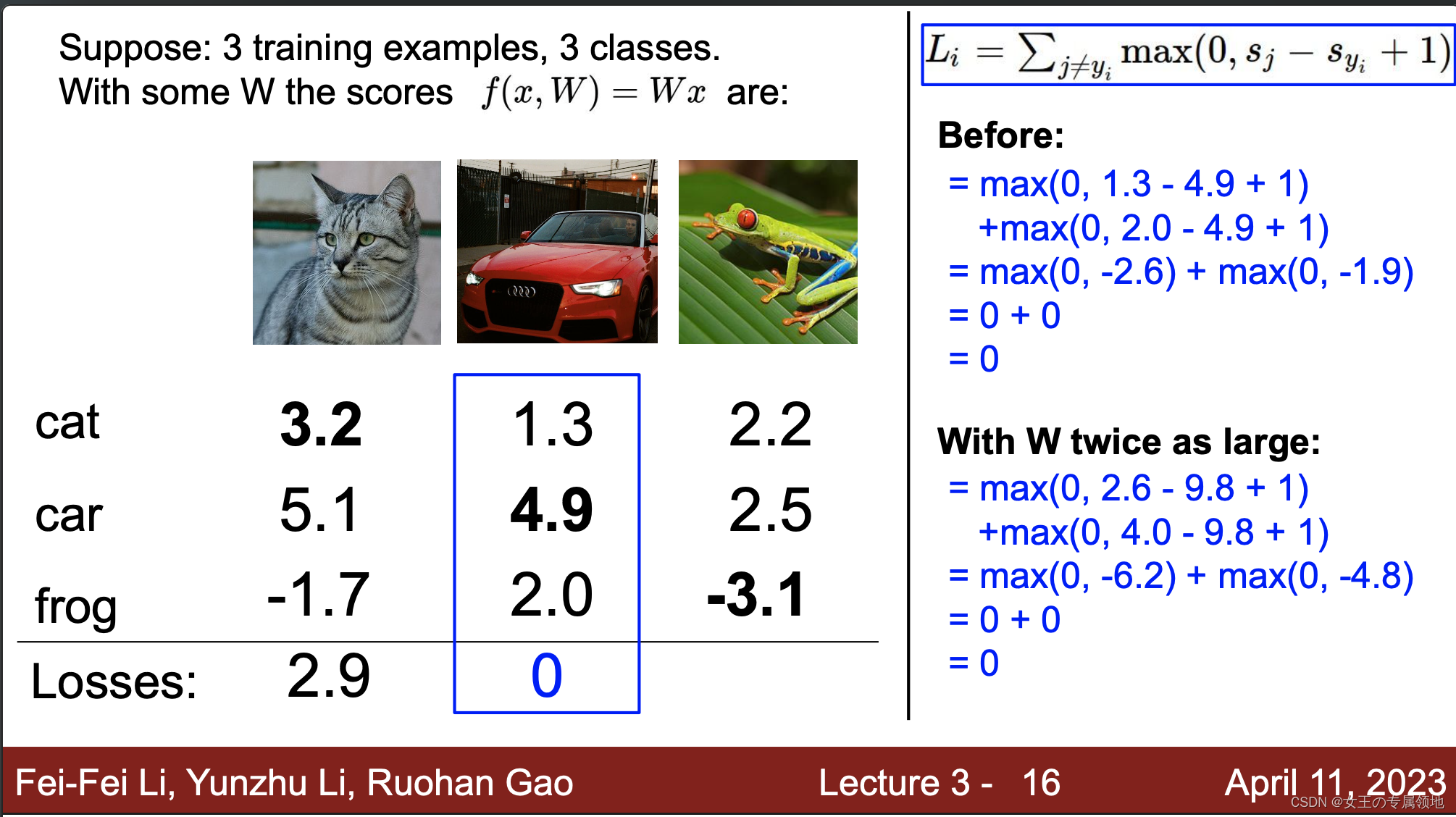

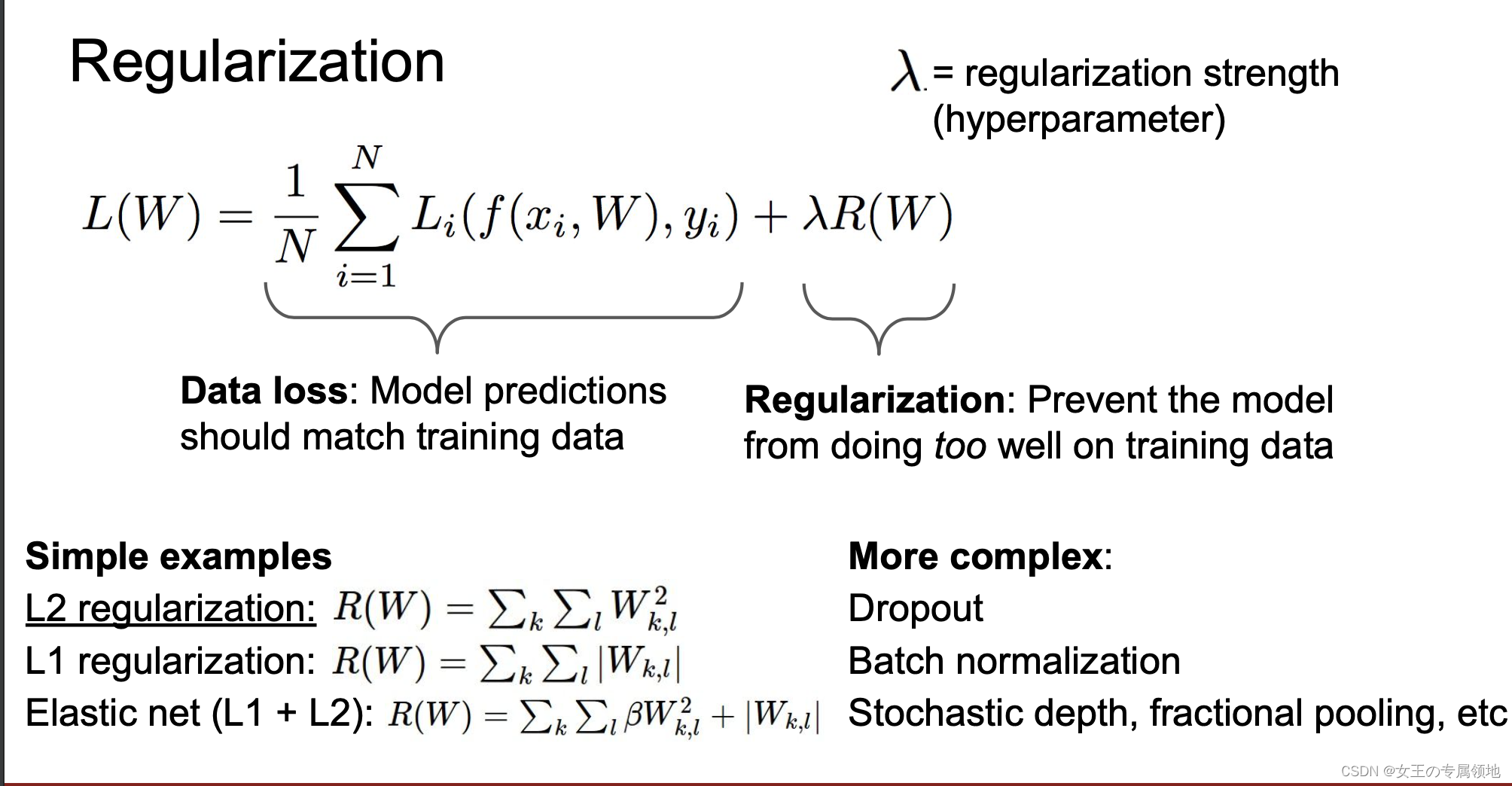
1.2 正则化损失(regularization loss)
为什么要正则化?
- 表达对权重的偏好
- 使模型简单,以便它适用于测试数据
- 通过添加曲率来改进优化


1.3 常见正则化损失
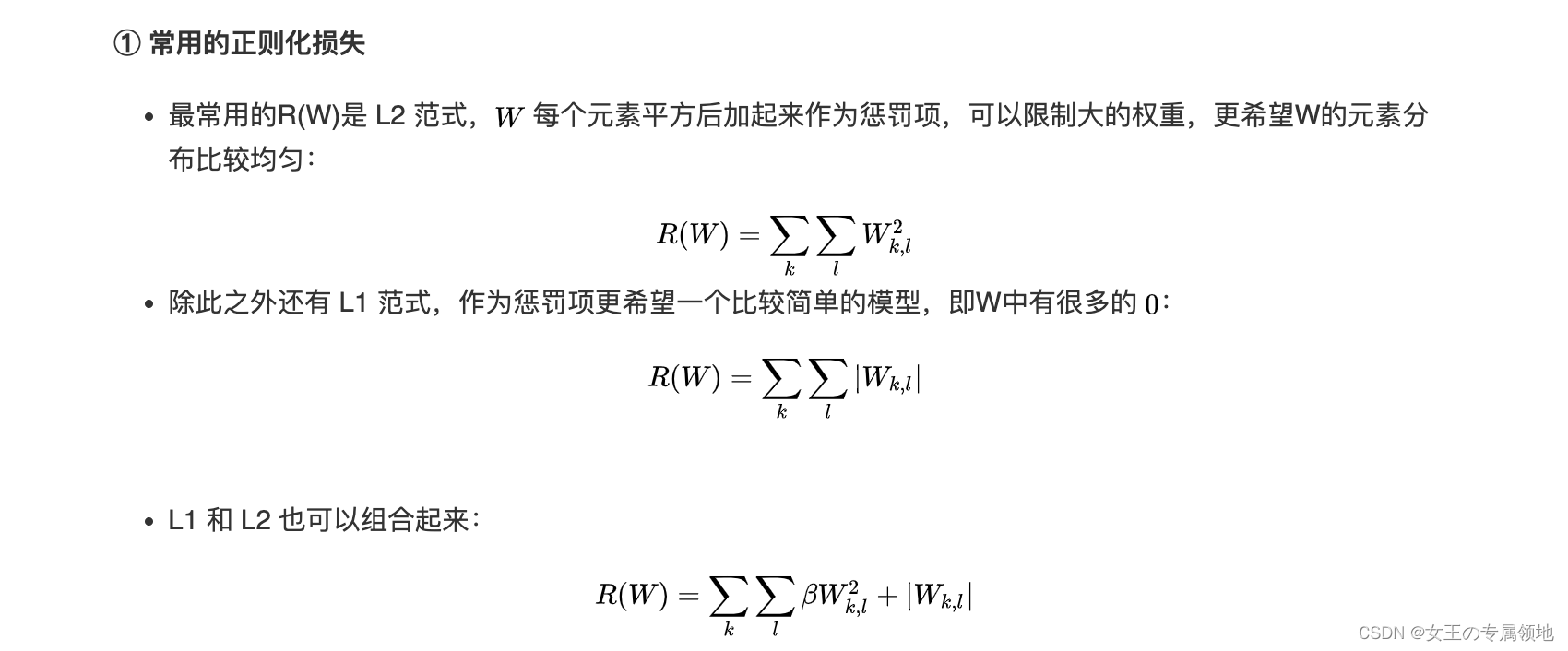

二、优化(Optimization)
🔥🔥🔥重要推荐:可视化工具 :http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/

现在我们有了数据集、评分函数、损失函数,那我们怎么找到最好的超参数W呢?答案是优化!
2.1 优化策略(Optimization Strategy)
优化策略的目标是:找到能够最小化损失函数值的权重W。
1) 策略一:随机搜索(Random search)
随机尝试很多不同的权重,然后看其中哪个最好。这是一个差劲的初始方案。验证集上表现最好的权重W跑测试集的准确率是15.5%,而完全随机猜的准确率是10%,效果不好!
思路调整:新的策略是从随机权重W开始,然后迭代取优,每次都让它的损失值变得更小一点,从而获得更低的损失值。想象自己是一个蒙着眼睛的徒步者,正走在山地地形上,目标是要慢慢走到山底。在 CIFAR-10 的例子中,这山是30730维的(因为W是3073X10)。我们在山上踩的每一点都对应一个的损失值,该损失值可以看做该点的海拔高度。
2) 策略二:随机本地搜索
第一个策略可以看做是每走一步都尝试几个随机方向,如果是上山方向就停在原地,如果是下山方向,就向该方向走一步。这次我们从一个随机W开始,然后生成一个随机的扰动aW,只有当 W+aW 的损失值变低,我们才会更新。用上述方式迭代1000次,这个方法可以得到 公式 的分类准确率。
3) 策略三:跟随梯度
前两个策略关键点都是在权重空间中找到合适的方向,使得沿其调整能降低损失函数的损失值。其实不需要随机寻找方向,我们可以直接计算出最好的方向,这个方向就是损失函数的梯度(gradient)。这个方法就好比是感受我们脚下山体的倾斜程度,然后向着最陡峭的下降方向下山。
在一维函数中,斜率是函数在某一点的瞬时变化率。梯度是函数斜率的一般化表达,它是一个向量。
在输入空间中,梯度是各个维度的斜率组成的向量(或者称为导数 derivatives)。对一维函数的求导公式如下:
三、梯度计算
计算梯度有两种方法:
1.数值梯度法,缓慢的近似方法,实现相对简单。
2. 分析梯度法,计算迅速,结果精确,但是实现时容易出错,且需要使用微分。
3.1 数值梯度法
数值梯度法是借助于梯度的定义对其进行逼近计算。输入函数
f
f
f和矩阵
x
x
x,计算
f
f
f的梯度的通用函数,它返回函数
f
f
f在点
x
x
x处的梯度,利用公式
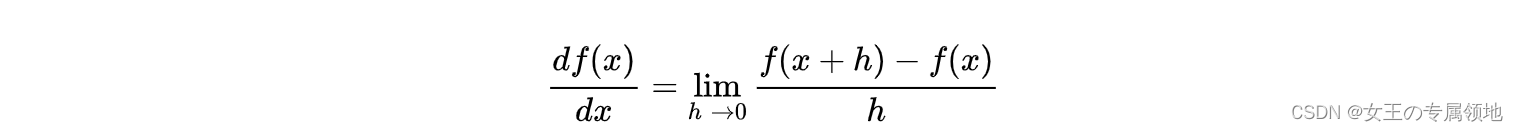
代码对
x
x
x矩阵所有元素进行迭代,在每个元素上产生一个很小的变化
h
h
h,通过观察函数值变化,计算函数在该元素上的偏导数。最后,所有的梯度存储在变量 grad 。实际中用中心差值公式(centered difference formula)
[
f
(
x
+
h
)
−
f
(
x
−
h
)
]
/
2
h
[f(x+h)-f(x-h)]/2h
[f(x+h)−f(x−h)]/2h 效果会更好。
① 在梯度负方向上更新
- 在上面的代码中,为了计算 W_new,要注意我们是向着梯度df的负方向去更新,这是因为我们希望损失函数值是降低而不是升高。(偏导大于0,损失递增,W需要减小;偏导小于0,损失递减,W需要增大。)
② 步长的影响
- 从某个具体的点W开始计算梯度,梯度指明了函数在哪个方向是变化率最大的,即损失函数下降最陡峭的方向,但是没有指明在这个方向上应该迈多大的步子。
- 小步长下降稳定但进度慢,大步长进展快但是风险更大,可能导致错过最优点,让损失值上升。在某些点如果步长过大,反而可能越过最低点导致更高的损失值。选择步长(也叫作学习率)将会是神经网络训练中最重要(也是最麻烦)的超参数设定之一。
③ 效率问题
- 计算数值梯度的复杂性和参数的量线性相关。在本例中有30730个参数,所以损失函数每走一步就需要计算30731次损失函数(计算梯度时计算30730次,最终计算一次更新后的。)
- 现代神经网络很容易就有上千万的参数,因此这个问题只会越发严峻。显然这个策略不适合大规模数据。
3.2 解析梯度法
数值梯度的计算比较简单,但缺点在于只是近似不够精确,且耗费计算资源太多。
得益于牛顿-莱布尼茨的微积分,我们可以利用微分来分析,得到计算梯度的公式(不是近似),用公式计算梯度速度很快,但在实现的时候容易出错。
为了解决这个问题,在实际操作时常常将分析梯度法的结果和数值梯度法的结果作比较,以此来检查其实现的正确性,这个步骤叫做梯度检查。

四、梯度下降(Gradient Descent)
现在可以利用微分公式计算损失函数梯度了,程序重复地计算梯度然后对参数进行更新,这一过程称为梯度下降。
4.1 Batch梯度下降法
Batch梯度下降法 (批梯度下降法) 是最常用的梯度下降形式,它是基于整个训练集的梯度下降算法,在更新参数时使用所有的样本来进行更新。
对整个训练集进行梯度下降法的时候,我们必须处理整个训练数据集,然后才能进行一步梯度下降,即每一步梯度下降法需要对整个训练集进行一次处理,如果训练数据集很大的时候,处理速度就会比较慢。
但是如果每次处理训练数据的一部分,基于这个子集进行梯度下降法,算法迭代速度会更快。而处理的这些一小部分训练子集即称为 Mini-Batch,这个算法也就是我们说的 Mini-Batch 梯度下降法。
4.2 Mini-Batch梯度下降法
Mini-Batch梯度下降法 (小批量梯度下降法) 每次同时处理单个的 Mini-Batch,其他与 Batch 梯度下降法一致。使用 Batch 梯度下降法,对整个训练集的一次遍历只能做一个梯度下降;而使用 Mini-Batch 梯度下降法,对整个训练集的一次遍历 (称为一个 epoch) 能做 Mini-Batch 个数个梯度下降。之后,可以一直遍历训练集,直到最后收敛到一个合适的精度。
例如,在目前最高水平的卷积神经网络中,一个典型的小批量包含 256 个样本,而整个训练集是一百二十万个样本。(CIFAR-10,就有 50000 个训练样本。)比如这个小批量数据就用来实现一个参数更新:
这个方法之所以效果不错,是因为训练集中的数据都是相关的。要理解这一点,可以想象一个极端情况:在ILSVRC中的120万个图像是1000张不同图片的复制(每个类别1张图片,每张图片复制1200次)。那么显然计算这1200张复制图像的梯度就应该是一样的。对比120万张图片的数据损失的均值与只计算1000张的子集的数据损失均值时,结果应该是一样的。实际情况中,数据集肯定不会包含重复图像,那么小批量数据的梯度就是对整个数据集梯度的一个近似。因此,在实践中通过计算小批量数据的梯度可以实现更快速地收敛,并以此来进行更频繁的参数更新。
⚠️小批量数据策略有个极端情况:每批数据的样本量为1,这种策略被称为随机梯度下降(Stochastic Gradient Descent 简称SGD),有时候也被称为在线梯度下降。SGD在技术上是指每次使用1个样本来计算梯度,你还是会听到人们使用SGD来指代小批量数据梯度下降(或者用MGD来指代小批量数据梯度下降)。
小批量数据的大小是一个超参数,但是一般并不需要通过交叉验证来调参。它一般设置为同样大小,比如32、64、128等。之所以使用2的指数,是因为在实际中许多向量化操作实现的时候,如果输入数据量是2的指数,那么运算更快。
可以看一下吴恩达老师的讲解,非常之详尽!!!https://www.showmeai.tech/article-detail/217
4.3 SGD+Momentum
-
Momentum
-
Nesterov Momentum
4.4 AdaGrad
4.5 RMSProp: “Leaky AdaGrad”
4.6 Adam
五、学习率(learning rate)
SGD, SGD+Momentum, Adagrad, RMSProp, Adam 都有超参数学习率。