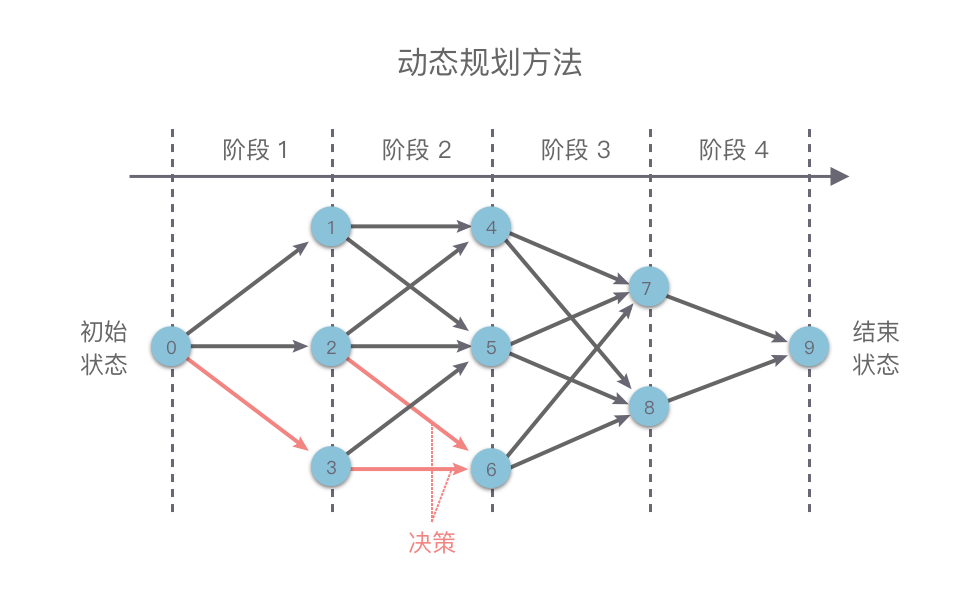
前面我们学习了图与网络分析的基础知识及经典问题,大家是否已经学会了呢?接下来小编和大家学习最后一个经典问题——最小费用最大流问题。
最小费用最大流问题是经济学和管理学中的一类典型问题。在一个网络中每段路径都有“容量”和“费用”两个限制的条件下,此类问题的研究试图寻找出:流量从A到B,如何选择路径、分配经过路径的流量,可以达到所用的费用最小的要求。
如n辆卡车要运送物品,从A地到B地。由于每条路段都有不同的路费要缴纳,每条路能容纳的车的数量有限制,最小费用最大流问题指如何分配卡车的出发路径可以达到费用最低,物品又能全部送到。
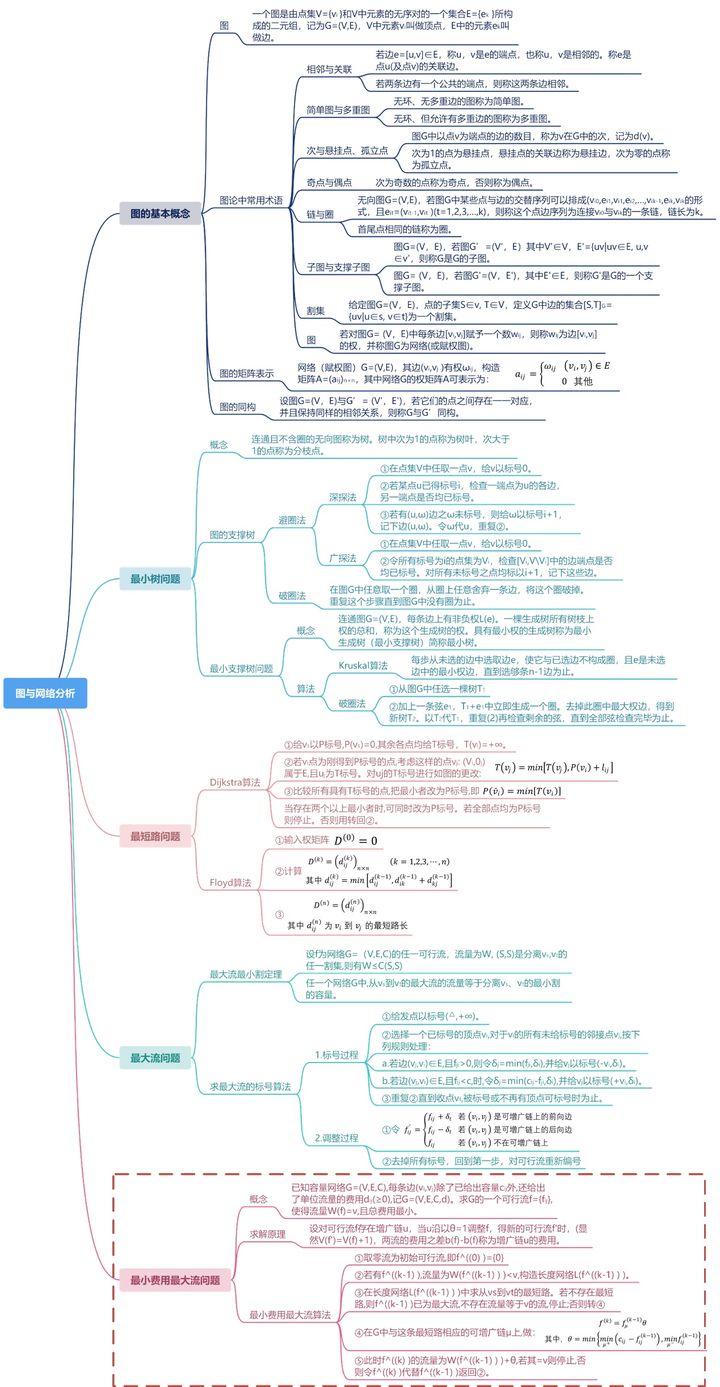
下面,让我们从实际问题出发,学习如何解决最小费用最大流问题吧!
一、问题描述及求解原理
01 问题描述
网络G=(V,E,C),每一弧(vi,vj)∈E,给出(vi,vj)上单位流的费用d(vi,vj)≥0(简记dij),记G=(V,E,C,d)。
最小费用最大流问题:
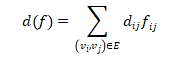
求一个最大流f,使流的总费用取最小值。
02 求解原理
设对可行流f存在增广链𝜇,当沿𝜇以θ=1调整f,得新的可行流f'时,显然V(f')=V(f)+1,两流的费用之差d(f)-d(fx27;):
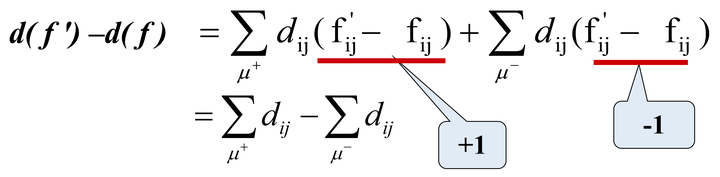
称为增广链𝜇的费用。
原理依据:
若f是流值为V(f)的所有可行流中费用最小者,而𝜇是关于f的所有增广链中费用最小的增广链,则沿𝜇以θ去调整f,得可行流f',f'就是流量为V(f)+θ的所有可行流中费用最小的可行流。这样,当f'是最大流时,f'就是所求的最小费用最大流。
如果已知f是流量为V(f)的最小费用流→求出关于f的最小费用增广链。
在构造最小费用增广链时,会将网络中的每一条条弧(vi,vj)都变成一对方向相反的弧,以形成四通八达的“路”,因此对于有向边(vi,vj)权wij按如下方法取值:
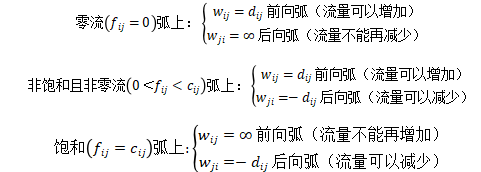
取值说明如下图所示:
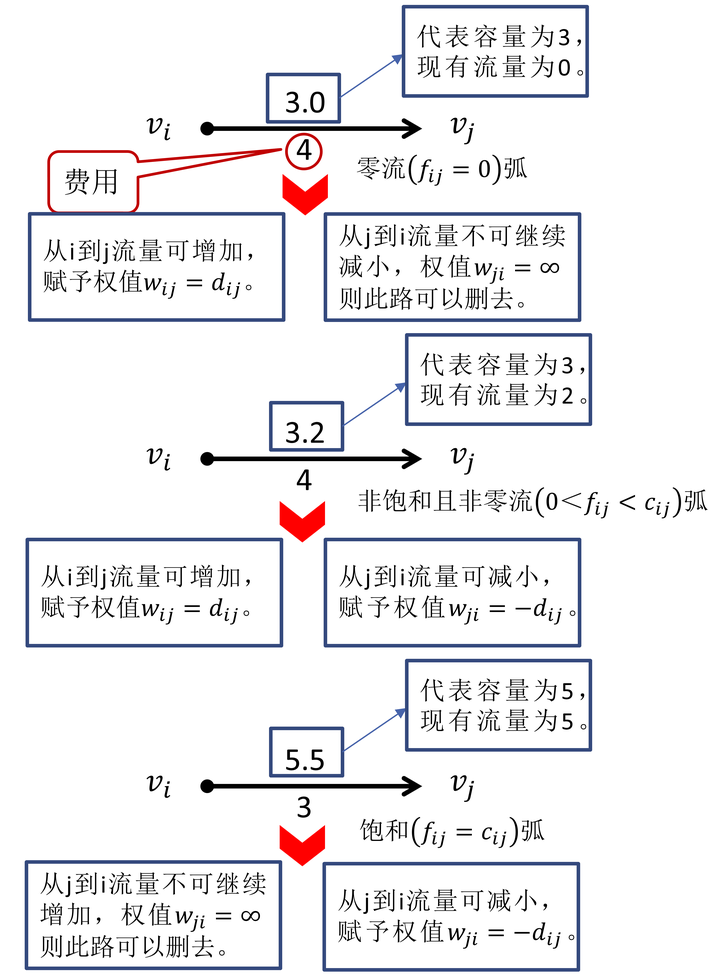
构造赋权有向图W(f),它的顶点是G的顶点,W(f)中弧及其权wij按弧(vi,vj)在G中的情形分为:

新网络W(f)成为流f的(费用)长度网络。
由增广链费用的概念及网络W(f)的定义,知在网络G中寻求关于可行流f的最小费用增广链,等价于在网络W(f)中寻求从vs到vt的最短路。
03 算法步骤
(1)根据网络中的费用首先确定费用最小的长度网络,将该长度网络确定为初始可行流f0=0,令k=0;
(2)应用流量网络对增广链进行调整,记经k次调整得到的最小费用流为fk,构造增量网络W(fk);
(3)在W(fk)中,寻找vs到vt的最短路。若不存在最短路(即最短路路长是∞),则fk就是最小费用最大流;若存在最短路,则此最短路即为原网络G中相应的可增广链𝜇,转入第4步。
(4)在增广链𝜇上fk按下式进行调整,调整量θ为:
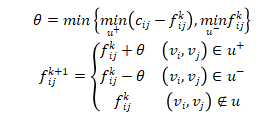
得新的可行流fk+1,返回第2步
二、实例应用
01 例题求解
例1:求下图所示网络的最小费用最大流。弧旁数字为(dij,cij)。
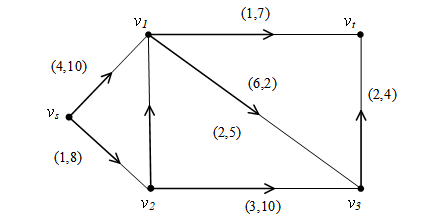
解:
(1)取初始可行流;
(2)按算法要求构造长度网络 ;
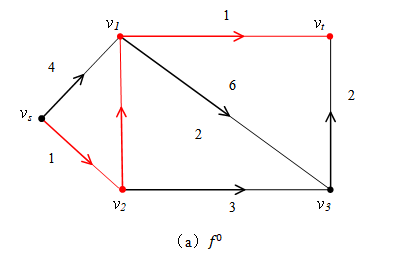
(3)在原网络G中,与这条最短路对应的增广链为 ;
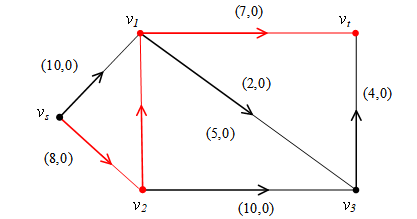
(4)在原网络D中,与这条最短路对应的增广链为 :
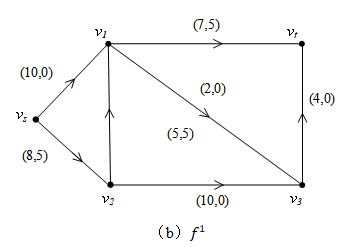
按照上述算法依次得 ,流量依次为
,构造相应的增量网络为
,如图(a),(e),(g),(i)所示。
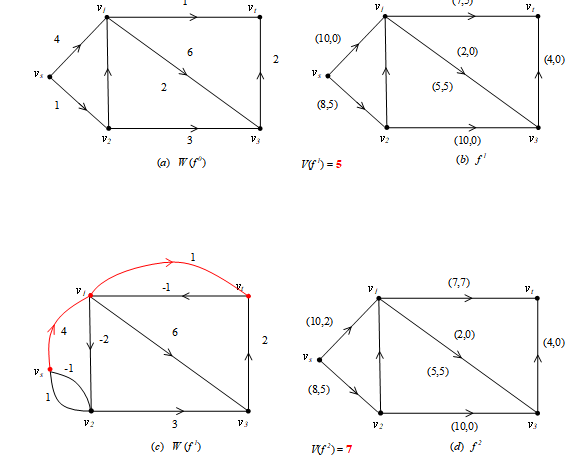
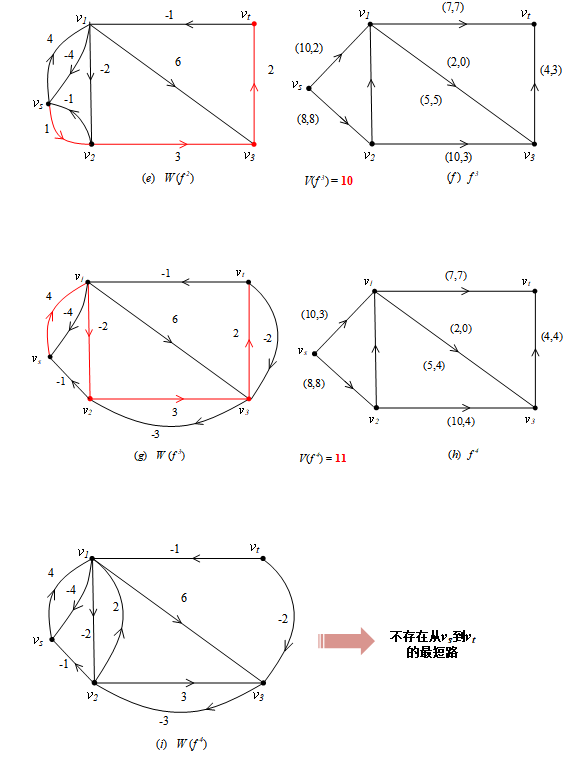
图(i)中,不存在从 到
的最短路,所以
为最小费用最大流。
02 拓展延伸
最小费用最大流问题还可以使用线性规划方法进行求解,思路如下:
(1)通过运筹说第78期相关介绍可以求出最大流量。
(2)在保证总流量等于最大流量的条件下,以最小化总费用为目标求出每条弧上的流量。
例2:某公司有一个管道网络如下图所示,使用这个网络可以将石油从产地v1送到销地v7,给出了每一段管道的容量cij(单位为:万加仑/小时),此外还给出了每段弧上的单位流量的费用dij(单位为:百元/万加仑),(cij,dij)在图的弧上已标出,如果使用这个网络从产地v1向销地v7运送石油,问怎样运送才能运送最多的石油且使总运费最小?
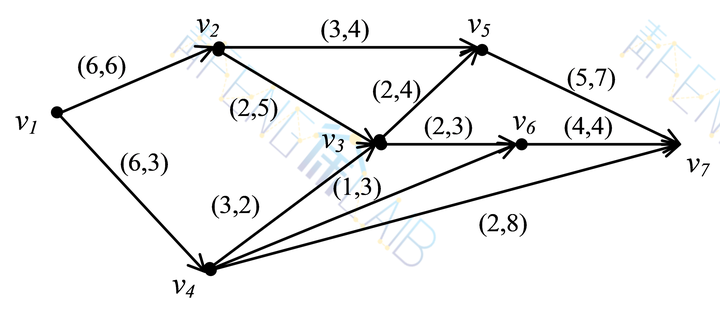
通过标号算法可以求出最大流量为10。然后,在保证总流量等于10的条件下,以最小化总费用为目标求出每条弧上的流量,如下所示:
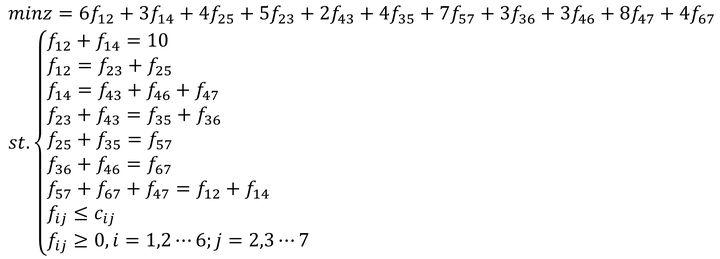
后续步骤使用线性规划求解方法如单纯形法求解即可。
以上就是最小费用最大流问题的全部内容了,通过本节学习大家是否对该问题有了一个初步的认识呢,是否可以求解最小费用最大流问题呢?下一次小编将带大家学习第九章——网络计划,敬请关注!
作者 | 张宇 齐鹏
责编 | 刘文志
审核 | 徐小峰