Aho-Corasick算法简称AC算法，也称为AC自动机(Aho-Corasick)算法，1975年产生于贝尔实验室（The Bell Labs），是一种用于解决多模式字符串匹配的经典算法之一。

the Bell Lab 

本文的运行效果：

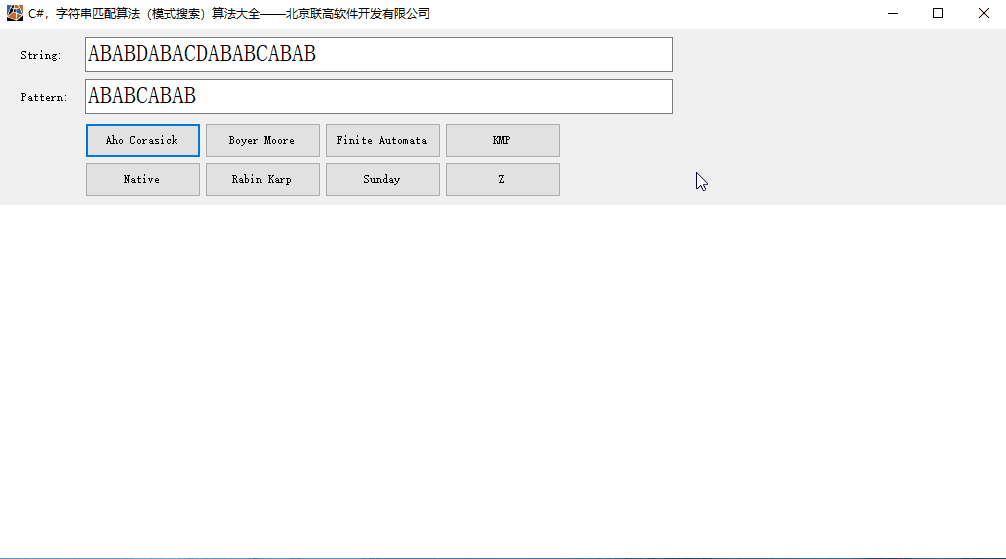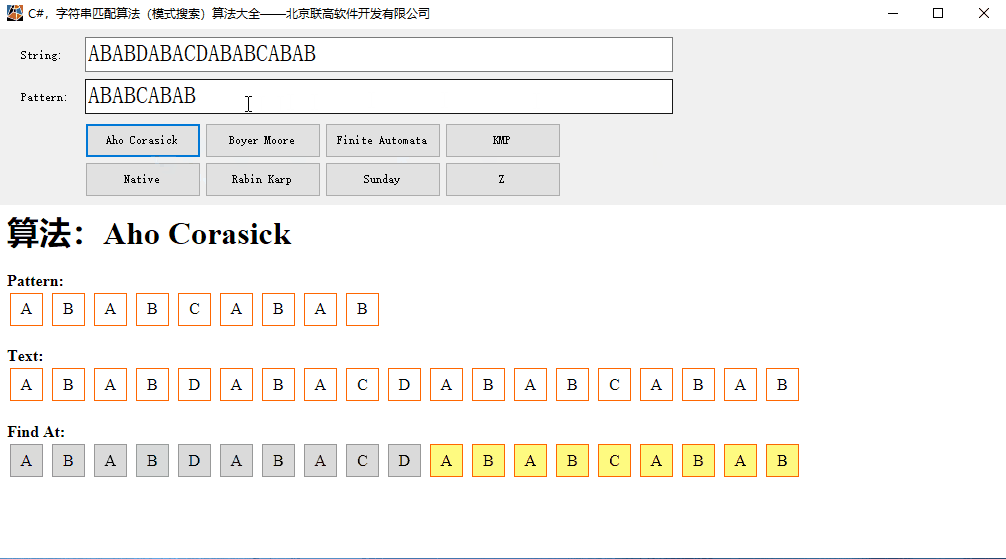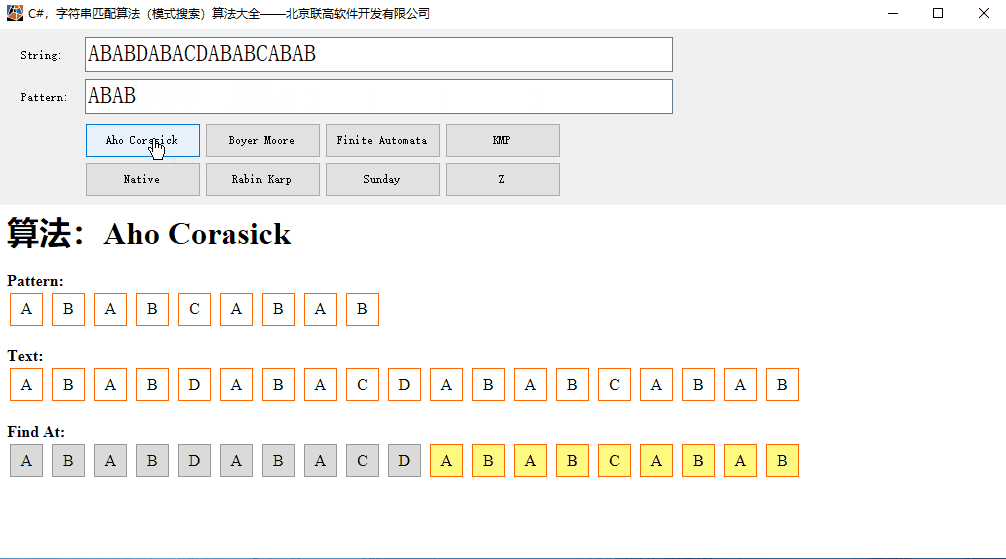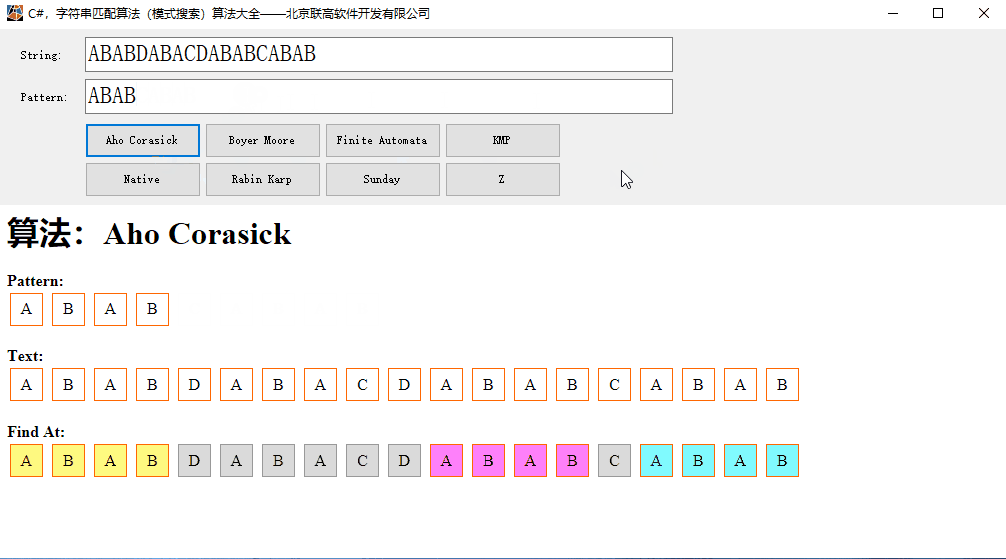
AC算法以模式树（字典树）Trie、广度优先策略和KMP模式匹配算法为核心内容。

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    /// <summary>
    /// Aho_Corasick 算法
    /// </summary>
    public static partial class PatternSearch
    {
        private static int MAXS = 512;
        private static int MAXC = 26;

        private static int[] outt = new int[MAXS];

        private static int[] f = new int[MAXS];

        private static int[,] g = new int[MAXS, MAXC];

        private static int buildMatchingMachine(string[] arr, int k)
        {
            for (int i = 0; i < outt.Length; i++)
            {
                outt[i] = 0;
            }

            for (int i = 0; i < MAXS; i++)
            {
                for (int j = 0; j < MAXC; j++)
                {
                    g[i, j] = -1;
                }
            }

            int states = 1;
            for (int i = 0; i < k; ++i)
            {
                string word = arr[i];
                int currentState = 0;

                for (int j = 0; j < word.Length; ++j)
                {
                    int ch = word[j] - 'A';
                    if (g[currentState, ch] == -1)
                    {
                        g[currentState, ch] = states++;
                    }
                    currentState = g[currentState, ch];
                }

                outt[currentState] |= (1 << i);
            }

            for (int ch = 0; ch < MAXC; ++ch)
            {
                if (g[0, ch] == -1)
                {
                    g[0, ch] = 0;
                }
            }

            for (int i = 0; i < MAXC; i++)
            {
                f[i] = 0;
            }

            Queue<int> q = new Queue<int>();
            for (int ch = 0; ch < MAXC; ++ch)
            {
                if (g[0, ch] != 0)
                {
                    f[g[0, ch]] = 0;
                    q.Enqueue(g[0, ch]);
                }
            }

            while (q.Count != 0)
            {
                int state = q.Peek();
                q.Dequeue();

                for (int ch = 0; ch < MAXC; ++ch)
                {
                    if (g[state, ch] != -1)
                    {
                        int failure = f[state];
                        while (g[failure, ch] == -1)
                        {
                            failure = f[failure];
                        }

                        failure = g[failure, ch];
                        f[g[state, ch]] = failure;

                        outt[g[state, ch]] |= outt[failure];

                        q.Enqueue(g[state, ch]);
                    }
                }
            }
            return states;
        }

        private static int findNextState(int currentState, char nextInput)
        {
            int answer = currentState;
            int ch = nextInput - 'A';

            while (g[answer, ch] == -1)
            {
                answer = f[answer];
            }
            return g[answer, ch];
        }

        public static List<int> Aho_Corasick_Search(string text, string pattern, int k = 1)
        {
            List<int> matchs = new List<int>();

            string[] arr = new string[1] { pattern };
            buildMatchingMachine(arr, k);

            int currentState = 0;

            for (int i = 0; i < text.Length; ++i)
            {
                currentState = findNextState(currentState, text[i]);

                if (outt[currentState] == 0)
                {
                    continue;
                }

                for (int j = 0; j < k; ++j)
                {
                    if ((outt[currentState] & (1 << j)) > 0)
                    {
                        matchs.Add((i - arr[j].Length + 1));
                    }
                }
            }

            return matchs;
        }
    }
}

POWER BY TRUFFER.CN

using System;
using System.Collections;
using System.Collections.Generic;

namespace Legalsoft.Truffer.Algorithm
{
    /// <summary>
    /// Aho_Corasick 算法
    /// </summary>
    public static partial class PatternSearch
    {
        private static int MAXS = 512;
        private static int MAXC = 26;

        private static int[] outt = new int[MAXS];

        private static int[] f = new int[MAXS];

        private static int[,] g = new int[MAXS, MAXC];

        private static int buildMatchingMachine(string[] arr, int k)
        {
            for (int i = 0; i < outt.Length; i++)
            {
                outt[i] = 0;
            }

            for (int i = 0; i < MAXS; i++)
            {
                for (int j = 0; j < MAXC; j++)
                {
                    g[i, j] = -1;
                }
            }

            int states = 1;
            for (int i = 0; i < k; ++i)
            {
                string word = arr[i];
                int currentState = 0;

                for (int j = 0; j < word.Length; ++j)
                {
                    int ch = word[j] - 'A';
                    if (g[currentState, ch] == -1)
                    {
                        g[currentState, ch] = states++;
                    }
                    currentState = g[currentState, ch];
                }

                outt[currentState] |= (1 << i);
            }

            for (int ch = 0; ch < MAXC; ++ch)
            {
                if (g[0, ch] == -1)
                {
                    g[0, ch] = 0;
                }
            }

            for (int i = 0; i < MAXC; i++)
            {
                f[i] = 0;
            }

            Queue<int> q = new Queue<int>();
            for (int ch = 0; ch < MAXC; ++ch)
            {
                if (g[0, ch] != 0)
                {
                    f[g[0, ch]] = 0;
                    q.Enqueue(g[0, ch]);
                }
            }

            while (q.Count != 0)
            {
                int state = q.Peek();
                q.Dequeue();

                for (int ch = 0; ch < MAXC; ++ch)
                {
                    if (g[state, ch] != -1)
                    {
                        int failure = f[state];
                        while (g[failure, ch] == -1)
                        {
                            failure = f[failure];
                        }

                        failure = g[failure, ch];
                        f[g[state, ch]] = failure;

                        outt[g[state, ch]] |= outt[failure];

                        q.Enqueue(g[state, ch]);
                    }
                }
            }
            return states;
        }

        private static int findNextState(int currentState, char nextInput)
        {
            int answer = currentState;
            int ch = nextInput - 'A';

            while (g[answer, ch] == -1)
            {
                answer = f[answer];
            }
            return g[answer, ch];
        }

        public static List<int> Aho_Corasick_Search(string text, string pattern, int k = 1)
        {
            List<int> matchs = new List<int>();

            string[] arr = new string[1] { pattern };
            buildMatchingMachine(arr, k);

            int currentState = 0;

            for (int i = 0; i < text.Length; ++i)
            {
                currentState = findNextState(currentState, text[i]);

                if (outt[currentState] == 0)
                {
                    continue;
                }

                for (int j = 0; j < k; ++j)
                {
                    if ((outt[currentState] & (1 << j)) > 0)
                    {
                        matchs.Add((i - arr[j].Length + 1));
                    }
                }
            }

            return matchs;
        }
    }
}