基于算术电路的全同态加密方案介绍
摘 要: 云计算技术目前已经发展得相对成熟,应用也逐步得到普及,它所具有的强大的数据处理能力,能够帮助个体用户计算复杂的数据。但它带来便利的同时,也催生了一系列用户隐私数据保护的问题。其中最为重要的便是数据安全问题。在用户将自己的隐私数据交给第三方处理时,需要将加密上传的数据进行解密,这样自己的数据是极有可能泄露的。全同态加密在密文处理上具有特殊的性质,即能够在不解密的情况下,对密文进行有效的计算。这对于用户数据的隐私保护有着极大的作用。本文主要介绍了全同态加密的发展历程,并着重讲述了第二代全同态加密方案的技术细节。
关键词:云计算;密码学;同态加密
An Introduction of fully homomorphic encryption scheme based on arithmetic circuits
Abstract: Cloud computing technology has been developed relatively mature, and its application has been gradually popularized. It has powerful data processing capability, which can help individual users calculate complex data. However, while it brings convenience, it has also given rise to a series of user privacy data protection issues. One of the most important issues is data security. When users hand over their private data to a third party for processing, they need to decrypt the encrypted uploaded data, so their data is highly likely to be leaked. Full homomorphic encryption has a special nature in ciphertext processing, i.e., it can effectively calculate the ciphertext without decrypting it. This has a great effect on the privacy protection of user data. In this paper, we introduce the development history of fully homomorphic encryption and focus on the technical details of the second generation fully homomorphic encryption scheme.
Keywords: Cloud Computing; Cryptography; Fully Homomorphic Encryption
**1 **背景
近年来,随着网络通信技术的不断发展,促使云计算和大数据的产生,这对于用户的隐私数据安全保护提出了新的问题和挑战。对于数据量很大的研究如机器学习、深度学习等来说,将数据放在个人电脑上计算是需要耗费很长的时间的。而云计算有着很大的优势,它提供可充分利用网络中的闲置计算资源,完成用户上传数据的计算需要。因此,用户需要将这些隐私的数据传送到云服务器上面执行计算任务。在传统的加密模式下,当用户需要与计算的强大计算力的时候,用户会首先将数据进行加密,并将解密密钥和加密信息一同传递至云端完成解密和计算,但如果这样做将会导致,用户的隐私数据完全的暴露给云平台,这显然不利于用户隐私数据的保护。
全同态加密是一种对密文进行计算的技术,也是安全多方计算的核心之一,它能够在不知道密钥的情况下,对密文进行计算,拿到想要的结果。这种奇特的性质使得全同态加密技术拥有广泛的实际运用,能够解决上述问题,还能在更多领域如隐私计算保护、密文检索、隐私集合求交等进行运用以解决实际问题。
尽管多年来密码学家们提出了许多支持对密文进行任意运算的密码方案,但是构造一个紧致的完全同态加密(Fully Homomorphic Encryption,FHE)方案仍然是十分困难的。
**2 **相关工作
FHE相关问题的提出最早可以追溯到1978年由Rivest, Adleman和Dertouzos[1]提出的利用同态加密的思想来保护数据信息的安全性,随后就相继诞生了许多部分同态加密方案。这些方案要么仅满足加法同态,要么仅满足乘法同态,还有部分能满足有限次加法与乘法的同态方案。
目前FHE的发展大致可以分为三个阶段,第一个阶段开始于Gentry在2009年博士毕业论文里提出的基于理想格的方案[2],后续的第一代方案本质上都是在各种环的理想上,先构建一个部分同态加密方案(Somewhat Homomorphic Encryption, SWHE),即方案由于计算时噪声的增长导致方案只能执行低次多项式的计算,然后依赖于稀疏子集和问题假设,进行压缩解密电路从而达到执行自己的解密函数进行同态解密。达到控制密文中噪声膨胀的目的。最后利用Gentry的核心思想“自举(Bootstrapping)”技术,在循环安全假设下得到FHE方案。
第二个阶段的FHE方案是基于算数电路和格加密的另一种假设错误学习问题(Learning With Errors,LWE),由两位大佬Brakerski和Vaikuntanathan提出,该方案体系使得方案构造更为简洁高效,其安全性可以归约到一般格上的标准困难问题。2011年,Brakerski和Vaikuntanathan基于LWE问题构造了BV11b方案[3],该方案通过使用一种重线性化(Re-linearization)技术密文计算时的扩张问题,通过使用维度-模约减(Dimension-Modulus Reduction)技术来将SWHE方案转化为FHE方案,无需使用压缩解密电路。2012年,Brakerski等人又共同构造了BGV12方案[4],该方案基于BV11的重现性化进行优化,提出了密钥交换(Key Switching)技术来解决密文运算中的密文扩张问题,并提出了模交换()技术以抑制密文运算中的噪声增长问题,将其稳定在一个合适的增长速率,无需使用Bootstrapping技术便能将SWHE方案化为层次型同态加密方案(Leveled Homomorphic Encryption,LHE),同时可以使用Bootstrapping技术达到FHE。这是一个重大转折,打破了Gentry原有的框架,效率上有了质的提升。而后,Brakerski等人又提出了BFV方案[5],该方案对比BGV方案,采用了最大比特编码技术,将噪声放到了最低位,将模交换技术内嵌入了密文乘法计算里,使得能完成更加深层次的密文计算。而后为了适应实数的需求,2017年韩国的Jung Hee Cheon等人又提出了CKKS方案[6],该方案是首个能处理复数和浮点数的同态加密方案,以前的方案都是在处理整数,该方案采用了定点近似计算技术使得处理结果为近似值,
另外还使用了重缩放技术(Rescale)来将密文还原并降低噪声消耗。
第三个阶段开启于2013年Gentry、Sahai 和 Waters的GSW方案[7],该方案基于LWE问题和布尔电路,但是采用了近似特征向量技术,构造出了矩阵形式的层次型同态加密方案,和以往的多项式形式大不同。该方案的无需密钥交换和模交换技术,采用了矩阵的乘法和加法,因而避免了之前方案中密文乘法造成的维度扩张问题,但运行效率要大大低于BGV和BFV。
再后面密码圈就百花齐放了,基于原来的三代全同态系统之上,出现了各种各样新的设计,致力于优化和加速BGV与GSW系统的运行效率。同态的发展路线如图1所示
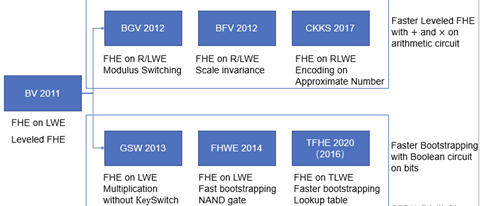
图1 FHE发展历程
**3 **技术内容介绍与分析
本文重点介绍目前最常用的第二代全同态加密方案的相关技术内容。
**3.1 **LWE与RLWE(Ring Learning With Errors)问题
在第二代FHE方案中,LWE问题是核心,很多方案都是基于这个问题而建立的,它还有一个环上的版本,称为RLWE问题,基于RLWE问题构建的方案比LWE问题更具有效率。
3.1.1 LWE问题
这是一个近似NP-hard问题,可以归约到格中的CVP(Closest Vector Problem)问题。
基础的概念如下,已知一个矩阵A以及一个向量e,求解方程。这里的e是一个固定数值范围内随机采集的一个随机噪音向量,所以这个问题就转化为通过A和b,来还原x。也就是理解为需要找到一组系数,使得一组基向量的线性组合无线逼近目标向量,使用噪音误差的大小来定义需要距离目标向量有多近。
LWE问题主要分为两类决策型LWE(DLWE)和搜索型LWE(SLWE)。二者难度相近,定义也很类似,但区别在于是否需要找出x。
SLWE问题定义为,随机从素数有限域取维矩阵A,随机从素数有限域取n维密钥s,随机从噪声最大值为B随机分布里取一个噪声e。然后给定,需要从中找到一个合理的使得。也就是可以理解为给定一个矩阵和带有误差的式子,从中计算出未知的密钥。
DLWE问题的定义很类似,不同之处是需要辨别出和,其中v是一个随机的变量,也就是说解决DLWE问题的关键是辨别出给定的数据究竟是一个LWE问题实例还是一组随机变量。
3.1.2 RLWE问题
RLWE问题是LWE问题在环上的版本,也就是A和s都选取是在多项式环上。由于多项式环中的每个项都是由多个元素组成,每一次的操作都相当于对多个元素进行操作,这样对比LWE每次仅能对一个元素操作来说能够大大的提升效率。这也是各大方案中SIMD(Single Instruction Multiple Data)操作的核心。
当然,RLWE问题也分为两个版本决策型和搜索型,基本定义和LWE问题的两个类型类似,这里就不多叙述了。
**3.2 **BGV12方案
BGV方案是由Brakerski等大佬12年提出的,是第二代FHE的一个重要里程碑。主要的核心是优化了BV11b方案里的Dimension-Modulus Reduction和Re-linearization技术,提出了Modulus Switching和Key Switching技术,这就使得无需Gentry的Bootstrapping技术也能够做到较多层数的同态乘法达到LFHE级别。
3.2.1 Key Switching技术
在BGV方案里,同态乘法被定义为了克罗内克积(Kronecker product),也叫做张积。因此在做密文乘法的时候会导致密文和私钥膨胀得很厉害,由此就诞生了Key Switching,核心是保持解密的消息基本不变,而将因为张量积膨胀的大密文和大密钥替换成小密文和小密钥。
Key Switching技术用到了一个核心操作称为扁平化操作(Flatten),实际上这个操作很多地方都要用,它包含两个重要的函数BitDecomp( )和Powerof2( ),前者的功能是将参数向量的每一维都拆为二进制表示,后者的功能则是把参数扩张为2的幂次乘以每一维的形式,这样能使得内积保持不变,同时能减小噪声。
Key Switching主要有两个步骤算法,第一个算法称为交换密钥生成算法,作用是输出一些能够将大密钥化为小密钥的辅助信息。第二个算法则是利用第一个算法的辅助信息,将大密文化为小密文。
3.2.2 Modulus Switching技术
密文计算中产生膨胀的不只是密文,随之而来的噪声也将会增长得很快,如果不采取措施,那么噪声的增长将是双指数级别的。而Modulus Switching正是用来控制噪声增长的,将噪声的增长削减为线性,变为很慢,无需自举,以达成一个LFHE方案。
Modulus Switching的核心是用模数链进行放缩,也就是设定一条模数链,其中的模数接近于噪声上限B,满足和原模数同余。在一次同态乘法后,噪声将会变为B2,那么这时候对结果除以模数,噪声就会变回B,这样每一次乘法都调用一次Modulus Switching,就能使得噪声基本维持不变。但是付出的代价就是计算的层数将由模数链的长度限制。
主要的算法是一个取整算法,即获取一个和密文向量同余的,最接近的一个整数向量。利用整个整数向量加上上述放缩步骤就组成了Modulus Switching。
3.2.3 同态方案
1)初始算法:初始算法主要是生成方案所必须的参数包含生成阶梯式的模数链,以及每一层的参数集(多项式阶数、噪声随机分布等)。
2)密钥生成算法:密钥生成算法要做的就是,生成每一层的私钥和公钥,接着生成每一层的密钥交换的辅助信息。
3)加密算法:使用参数集对明文进行加密,核心是将明文加密到LWE实例上去。
4)解密算法:可以根据层数选择对应的私钥,进行解密,还原明文。
5)刷新算法:这个算法中包含了Modulus Switching和Key Switching,就是用来解决密文扩张和噪声增长过快的问题。每一次乘法计算都调用一次,能够使得计算能力得到增加。
**3.3 **BFV方案
BFV依旧是基于LWE问题,对比于BGV方案,它采用了最大比特编码,也就是将明文消息编码到了高位。其次,是它取消了模数必须为素数的限制,无需Modulus Switching,将这一步骤直接加入到了密文乘法运算中。但由于所有的运算都是在整数之上,所以运算速度会比BGV慢,但是由于更加优秀的噪声控制,会使得电路的深度更深。同样BFV也对密文的扩张进行了处理,使用的是和Key Switching类似的Re-linearization算法。
3.3.1 Re-linearization算法
在BFV方案里的同态乘法中,两个具有两项的密文相乘之后将得到一个新的三项密文,这对比之前的密文增加了一项,如果不想加以控制,这个项数将随着乘法次数的增加而增加的很快。Re-linearization算法就是一个控制项数的算法。其核心是把密文乘积增加的第三项平方项使用一个修补项进行代替,这个修补项能够和其他两项进行合并而不会影响解密的结果,这样就能将三项化为两项,以达到削减密文规模的目的。
3.3.2 同态方案
1)初始算法:初始算法主要是生成方案所必须的参数包含每一层的参数集(多项式阶数、噪声随机分布等),注意这里没有模数链了,BFV无需模交换。
2)密钥生成算法:这里的密钥生成算法要生成的就是初始的加密公钥,用于Re-linearization的评估密钥链,还有用于最终解密的私钥。
3)加密算法:使用参数集对明文进行加密,核心是将明文加密到LWE或RLWE实例上去。
4)解密算法:使用最终的私钥,进行解密,还原明文。
5)重线性化算法:在每一次乘法计算后,需要调用这个算法,来削减密文的规模。
**3.4 **CKKS方案
因为实际的大部分场景使用的是浮点数,而更多需要的不是精确的结果,而是一个大致的近似值,而BGV和BFV方案不能满足这个需求。于是在2017年,韩国的学者提出了CKKS方案。此方案是一个近似精度计算的方案,允许复数和实数计算。它的核心思想是,将加密产生的噪声视为近似计算误差的一部分,也就是解密出来的结果可以直接视为原始消息的近似值,它在加密之前将消息乘以了一个缩放因子,这样可以保障在计算时的精确度,并在后续计算后使用Rescale算法来将缩放变回去,还能顺带削减一部分低位噪声。当然对于密文的规模控制,也使用了Re-linearization算法。对比前面的BGV和BFV算法,CKKS的编码也是很不同的。
3.4.1 CKKS的编码
一般的基于RLWE同态算法如BGV、BFV等的明文空间都是整数多项式,而CKKS由于是进行复数(实数)计算,它的消息空间是复数空间,且维度只有前两个方案的一半,为此,需要将消息从复数向量给“编码”成整数多项式。
首先是将消息的维度扩充一倍,方法是将取出的原消息取共轭然后拼接到原消息上面。接着是乘以一个缩放因子,用于放大小数部分,确保后续计算的精确度,最后才是将它转变为多项式。
3.4.2 Rescale算法
需要使用这个算法的原因是在之前的编码步骤里将消息乘以了一个缩放因子,一次乘法过后这个因子将变为平方项,显然会对还原明文信息造成影响,所以需要除以这个缩放因子。CKKS采用的做法和BGV方案有点类似,它使用了一条模数链,里面的模数大小和缩放因子接近,每一次Rescale都将除以一个模数,并将这个模数从模数链上去除。由于是对密文使用,密文中包含的噪声也同步进行了缩放,也就是缩小了噪声。当然这也使得CKKS具有BGV一样的诟病,方案能计算的深度受限制于模数链长度。
3.4.3 同态方案
1)编码:将消息编码为整数多项式。
2)初始算法:初始算法主要是生成方案所必须的参数包含生成阶梯式的模数链,以及每一层的参数集(多项式阶数、噪声随机分布等)。
3)密钥生成算法:这里的密钥生成算法要生成的就是初始的加密公钥,用于Re-linearization的评估密钥链,还有用于最终解密的私钥。
4)加密算法:使用参数集对明文进行加密,核心是将明文加密到LWE或RLWE实例上去。
5)解密算法:使用最终的私钥,进行解密,还原明文。
6)重线性化算法:在每一次乘法计算后,需要调用这个算法,来削减密文的规模。
7)重缩放算法:将密文的缩放因子变为原样并进一步缩减噪声。
**4 **总结
目前主流的算术电路同态方案还是都是基于LWE和RLWE的,最常用的就是BGV、BFV和CKKS,三者各有千秋,但终归效率比较低,而且对于目前的FHE来说,Bootstrapping的开销很大,所以一般都还是用的LFHE方案。当然还有其他类型的同态加密方案,如基于布尔电路的以FHEW和TFHE为代表的方案,优点是能够运行任意的函数,能够快速的Bootstrapping,但也有相应的不足,它们对多项式打包很不友好。对于目前的同态研究,主流还是CKKS的安全性问题、布尔电路方案和算术电路方案结合、快速自举、将同态与MPC结合、硬件上实现同态加速等等。
参 考 文 献
[1] Rivest R L, Adleman L, Dertouzos M L. On data banks and privacy homomorphisms[J]. Foundations of secure computation, 1978, 4(11): 169-180
[2] Gentry C. Fully homomorphic encryption using ideal lattices[C]. STOC. 2009, 9(2009): 169-178.
[3] Brakerski Z, Vaikuntanathan V. Efficient fully homomorphic encryption from (standard) LWE[C]. Proc of the 52nd Annual Symposium on Foundations of Computer Science. Washington DC: IEEE Computer Society, 2011: 97-106
[4] Brakerski Z, Gentry C, Vaikuntanathan V. (Leveled) fully homomorphic encryption without bootstrapping[C]. Proc of the 3rd Innovations in Theoretical Computer Science Conference. NewYork: ACM, 2012: 309-325.
[5] Brakerski Z. Fully homomorphic encryption without modulus switching from classical GapSVP[C]. In: Advances in cryptology–CRYPTO 2012. Springer, Berlin, Heidelberg, 2012: 868-886
[6] Jung Hee Cheon, Andrey Kim, Miran Kim, and Yongsoo Song. 2017. Homomorphic encryption for arithmetic of approximate numbers. In Int’l Conf. on the Theory and Application of Cryptology and Information Security. Springer, 409–437
[7] Gentry C, Sahai A, Waters B. Homomorphic encryption from learning with errors: Conceptually-simpler, asymptotically-faster, attribute-based [C]. Advances in Cryptology–CRYPTO 2013, LNCS, Springer Berlin Heidelberg, 2013: 75-92