题目
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例
- 输入:
lists = [[1,4,5],[1,3,4],[2,6]] - 输出:[1,1,2,3,4,4,5,6]
- 解释:链表数组如下:[ 1->4->5, 1->3->4, 2->6]将它们合并到一个有序链表中得到。1->1->2->3->4->4->5->6
题解
题目很好理解,其实方法也很好实现,但是对于优先队列的方法还是有一些疑惑。这个题目的题意很容易理解,该题目的主要有两类方法,一类是直接利用有序队列存储所有有序列表的值,然后基于有序队列构建一个新的满足要求的链表,该方法有些取巧;一类是把多链表合并转换成两个有序链表合并的问题(leetcode 21),该类方法还可以利用分治方法进行优化。下面分别对每类方法及其复杂性进行详细分析。
方法1
方法1 明确要根据k个有序链表构建一个有序列表。首先想到的是遍历k个链表的值逐一的加入到一个list中,然后对list进行降序排序。再从队尾逐个取数构建一个新链表。这个方法比较容易想到,而且比较好实现。代码如下:
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
#新建一个list存储所有链表的值
heap=[]
#遍历lists中所有链表的值,逐个加入到heap列表中
for sub_list in lists:
while sub_list:
heap.append(sub_list.val)
sub_list=sub_list.next
#对heap进行降序排序
heap.sort(reverse=True)
#新建一个链表
head=ListNode(None)
curr_list=head
while heap:
#从heap列表的尾部取最小数加入到链表中
temp_list=ListNode(heap.pop())
curr_list.next=temp_list
curr_list=curr_list.next
return head.next
复杂性分析:
假设k个链表中每个链表的长度最长为n。
- 时间复杂性:时间复杂主要有三块,一部分是遍历k个链表的所有值时间复杂性为 O ( k n ) O(kn) O(kn),然后是排序复杂性为 O ( k n ∗ l o g ( k n ) ) O(kn*log(kn)) O(kn∗log(kn)),最后构建新链表的复杂性相当于遍历一遍有序链表复杂性也为 O ( k n ) O(kn) O(kn)。因此整个算法的时间复杂性为 O ( k n ∗ l o g ( k n ) ) O(kn*log(kn)) O(kn∗log(kn))。
- 空间复杂性:空间复杂性主要是新构建的链表空间复杂性为 O ( k n ) O(kn) O(kn)。
方法1的优化(官方有序列表)
官方代码中关于有序列表的介绍这里采用heapq来实现有序列表,也就是把上面方法的列表用heapq最小堆来实现。整体思路没有大的变化,代码如下:
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
import heapq
#把lists所有数据入heapq
heap=[]
for list_1 in lists:
while list_1:
heapq.heappush(heap,list_1.val)
list_1=list_1.next
#从heapq中逐个取数据构建有序链表
curr_list=ListNode(None)
head=curr_list
while heap:
#逐个取最小的数据
temp_node=ListNode(heapq.heappop(heap),None)
curr_list.next=temp_node
curr_list=curr_list.next
return head.next
复杂性分析:
假设k个链表中每个链表的长度最长为n。
- 时间复杂性:时间复杂主要有两块,一部分是构建heapq的最小堆,复杂性为 O ( k n ∗ l o g ( k n ) ) O(kn*log(kn)) O(kn∗log(kn)),然后构建新链表的复杂性相当于遍历一遍有序链表复杂性也为 O ( k n ) O(kn) O(kn)。因此整个算法的时间复杂性为 O ( k n ∗ l o g ( k n ) ) O(kn*log(kn)) O(kn∗log(kn))。可以看到利用heapq与前面直接使用list再排序其实复杂性是一样的。
- 空间复杂性:空间复杂性主要是新构建的链表空间复杂性为 O ( k n ) O(kn) O(kn)。
方法1 优化2
最小堆其实还有一种线性复杂度的构建方法heapify。下面是代码实现:
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
#使用一个队列存储
heap=[]
for sub_list in lists:
while sub_list:
heap.append(sub_list.val)
sub_list=sub_list.next
#对heapify进行堆排序
import heapq
heapq.heapify(heap)
print(heap)
#heap.sort(reverse=True)
head=ListNode(None)
curr_list=head
while heap:
temp_list=ListNode(heapq.heappop(heap))
curr_list.next=temp_list
curr_list=curr_list.next
return head.next
复杂性分析:
假设k个链表中每个链表的长度最长为n。
- 时间复杂性:时间复杂主要有三块,一部分是遍历k个链表的所有值时间复杂性为 O ( k n ) O(kn) O(kn),然后是利用heapify构建最小堆复杂性为 O ( k n ) O(kn) O(kn),最后构建新链表的复杂性相当于遍历一遍有序链表复杂性也为 O ( k n ) O(kn) O(kn)。因此整个算法的时间复杂性为 O ( k n ) O(kn) O(kn)。这里复杂性有明显提升,但是跑的效果跟前面两种方法没有本质区别。
- 空间复杂性:空间复杂性主要是新构建的链表空间复杂性为 O ( k n ) O(kn) O(kn)
方法2:
在介绍k个有序链表的合并前需要简单介绍下两个链表的有序合并(leetcode21)方法。如果不考虑时间复杂性与空间复杂性实现的方法比较简单,这里要求时间复性为
O
(
n
)
O(n)
O(n),空间复杂性为
O
(
1
)
O(1)
O(1)。以示例中的前两个链表为例来说明相关过程。
首先,需要定义一个head链表头来作为最终结果链表的表头。
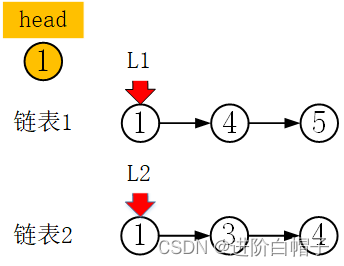
对比两个链表的当前节点的值,取小的作为head的next。先选择当前的l1加入到head链表中,然后l1跳到下一个节点。
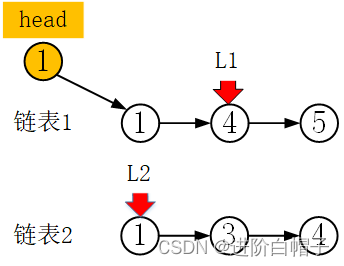
再比较当前的L1与l2值的大小。
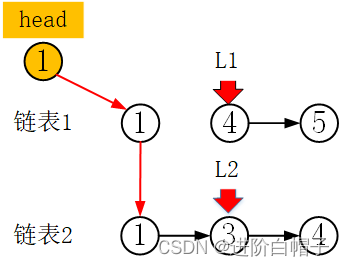
重复整个过程真到最后:
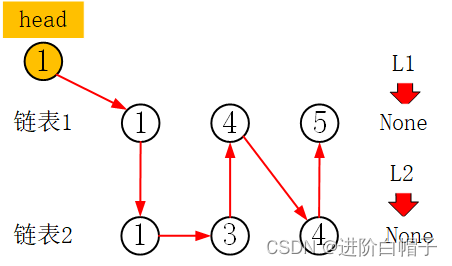
代码如下:
class Solution:
#合并两个链表leetcode 21
def merge2Lists(self,list1,list2):
head=ListNode(0)
curr_list=head
while list1 and list2:
if list1.val<list2.val:
curr_list.next=list1
list1=list1.next
else:
curr_list.next=list2
list2=list2.next
curr_list=curr_list.next
if list1:
curr_list.next=list1
if list2:
curr_list.next=list2
return head.next
下面基于两个有序列链表的合并方法来实现k个有序链表的合并。方法也很简单,逐个的对k链表两两合并。代码实现如下:
class Solution:
#合并两个链表leetcode 21
def merge2Lists(self,list1,list2):
head=ListNode(0)
curr_list=head
while list1 and list2:
if list1.val<list2.val:
curr_list.next=list1
list1=list1.next
else:
curr_list.next=list2
list2=list2.next
curr_list=curr_list.next
if list1:
curr_list.next=list1
if list2:
curr_list.next=list2
return head.next
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
n=len(lists)
ans=None
for i in range(n):
ans=self.merge2Lists(ans,lists[i])
return ans
复杂性分析:
- 时间复杂性:这里的时间复杂性相跟两个链表合并的长度有关,还是假设k为链表个数,n为每个链表的长度,第一次合并后,ans的长度为n,第二次合并后,ans的长度为2n,第i次合并ans的长度是i*n。因此总的代价为所有之和 O ( k 2 ∗ n ) O(k^2*n) O(k2∗n)
- 空间复杂度与两个链表一样,没有额外的空间资源占用 ( 1 ) (1) (1)
方法2优化
显示两两链表依次合并复杂性可以利用分治进行优化,可以减少一定的复杂性。官方有图比较明确这里就不再细说。代码如下:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
#合并两个链表leetcode 21
def merge2Lists(self,list1,list2):
head=ListNode(0)
curr_list=head
while list1 and list2:
if list1.val<list2.val:
curr_list.next=list1
list1=list1.next
else:
curr_list.next=list2
list2=list2.next
curr_list=curr_list.next
if list1:
curr_list.next=list1
if list2:
curr_list.next=list2
return head.next
def dac(self,lists,l,r):
if l==r:
return lists[l]
if l>r:
return None
m=(l+r)//2
return self.merge2Lists(self.dac(lists,l,m),self.dac(lists,m+1,r))
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
n=len(lists)
if n==0:
return None
if n==1:
return lists[0]
return self.dac(lists,0,len(lists)-1)
这里需要注意的是边界的两种特殊情况,一种是列表是空,一种是k个链表为空的情况。
复杂性分析:
- 时间复杂性:第一轮合并 k / 2 k/2 k/2 组链表,每一组的时间代价是 O ( 2 ∗ n ) O(2*n) O(2∗n),第二轮是合并 k / 4 k/4 k/4 组链表,每一组的时间代价是 O ( 4 ∗ n ) O(4*n) O(4∗n)。依次所有的时间代价之处为O(kn*logk)$
- 空间复杂度与两个链表一样,没有额外的空间资源占用 O ( l o g k ) O(logk) O(logk)