李宏毅-预测PM2.5

---

1 实验目的

巩固课堂所学知识，学习使用Linear Regression中梯度下降预测模型，并将所学运用至实践，根据从空气质量监测网下载的观测数据，使用Linear Regression 预测出空气污染指数(即PM2.5) 的数值。

---

2 实验要求

•不可以使用numpy.linalg.lstsq

•可以使用pandas库读取csv文件数据信息(其他库亦可)

•必须使用线性回归，方法必须使用梯度下降法

•可以使用多种高阶的梯度下降技术（如Adam、Adagrad等）

•程序运行时间不得大于3分钟

---

3 实验环境

3.1 硬件环境

笔记本电脑、Intel Core i5

3.2 软件环境

windows10操作系统、Python 3.8 64-bit、Visual Studio Code

---

4 实验原理

4.1 z-score标准化

$$\begin{gathered} \sigma =\sqrt{\frac{1}{\mathrm{N}}\sum _{i=1}^{\mathrm{N}}{\left({\mathrm{x}}_{\mathrm{i}}-\mu \right)}^2} \\ {\mathrm{z}}_{\mathrm{i}}=\frac{{\mathrm{x}}_{\mathrm{i}}-\mu }{\sigma } \end{gathered}$$

4.2 损失函数

$$L=\frac{1}{n}\sum _{i=0}^{n-1}{\left(y^n-\sum _{j=0}^k{w}_j{x}_j-b\right)}^2$$

4.3 偏微分

$$\begin{gathered} \frac{\partial \mathrm{L}}{\partial {\mathrm{w}}_j}=\frac{1}{n}\sum _i^{n-1}\left(y^i-\sum _{j=0}^k{w}_j{x}_j-b\right)\left(-x_j\right) \\ \frac{\partial \mathrm{L}}{\partial \mathrm{b}}=\frac{1}{n}\sum _{i=0}^{n-1}{\left(y^i-\sum _{j=0}^k{w}_j{x}_j-b\right)}^{\ast }(-1) \end{gathered}$$

4.4 参数迭代

$$\begin{gathered} \begin{array}{l}{w}_{\text{newi }}=w_i-{\eta }_w\frac{\partial L}{\partial w_i}\\ b_{\text{new }}=b-{\eta }_b\frac{\partial L}{\partial b}\end{array} \\ \begin{array}{l}if\left({\frac{dL}{dw}|}_{w=w^i}==0\right)\text{ then stop; }\end{array} \end{gathered}$$

4.5 Adagrad梯度更新优化算法

$${\eta }_n=\frac{\eta }{\sqrt{{\sum }_{i=1}^{n-1}{g}^{{\mathrm{i}}^2}}}$$

---

5 数据处理

5.1 读取训练数据.csv文件

这一步我们使用pandas库提供的函数提取训练数据，并对数据作初步处理，将一些无用指标剔除，以及将字符串数据转换为整数，方便之后的数学运算。

#读取数据csv文件，data类型为矩阵
data = pd.read_csv("train.csv")
#数据切片，去掉前三列无用且不方便数据处理的信息(日期、站点和测项)
data = data.iloc[:, 3:]
#为了数学运算方便，将FAINFULL为NR的值转换为0
data=data.replace(["NR",[0]])
#将data转换为numpy矩阵，规模为12(months)*20(days)*18行×24列
arr_data = data.to_numpy()

最后还需要将数据转为numpy库的矩阵类型，方便之后进一步的处理和更快的数学运算。

打印切片提取出的所有数据构成的array，确定处理无误：

5.2 整理训练数据

由于.csv中的数据是按照每天分散开的，题目要求给出连续9小时的数据预测第10小时的PM2.5数据，为了增大训练集的规模，拥有更多的训练数据，达到更好的训练效果，我们把同一个月的每一天数据连接起来：

#创建字典以月份为索引将同一个月的0-24小时数据连接起来
#大大增加了训练集的规模，模型可以更好地达到训练效果
month_data = {}
for month in range(12):
    #创建一个空的矩阵存放特征值
    #20天0-24时的数据共20*24行，18个特征共18列
    sample = np.empty([20*24,18])
    for day in range(20):
        #使用transpose()转置数据矩阵
        sample[(day*24):(day+1)*24,:] = arr_data[18 * (month*20 + day) : 18 * (month*20 + day + 1), :].transpose()
    #将整理好的数据集对应到字典中的月份索引
    month_data[month] = sample

5.3 划分模型输入和输出

矩阵x作为输入，在不同模型下有不同的规模（以模型A为例），矩阵y作为输出，即第10小时的PM2.5数值：

#创建一个空的矩阵用于存放训练集的输入，每连续9个小时为一组训练数据
#每个月有471组10小时训练数据，共12*471行
#每行是一组9个小时训练数据，1个小时有18个特征，矩阵共9*18列
#矩阵的元素类型为float
x = np.empty([12*471,9],dtype=float)
#训练集的输出矩阵，同样共12*471行，但不包含特征值，只有1列第10个小时的PM2.5的数据
#矩阵的元素类型为float
y = np.empty([12*471,1],dtype=float)
#为数据集赋值
for month in range(12):
    for day in range(20):
        for hour in range(24):
            #判断是否为这个月的数据最后一天的最后一组数据
            if day == 19 and hour > 14:
                continue
            #对训练集x和y进行赋值，reshape将数据转变为一行
            x[month*471 + day*24 + hour, :] = month_data[month][day*24 + hour : day * 24 + hour + 9,9].reshape(1, -1)  
            y[month*471 + day*24 + hour, 0] = month_data[month][day*24 + hour + 9, 9]

5.4 z-score标准化

Z-Score通过（x-μ）/σ将两组或多组数据转化为无单位的Z-Score分值，使得数据标准统一化，提高了数据可比性，削弱了数据解释性:

#每一个特征的平均值
mean_x = np.mean(x, axis=0)
#每一个特征的标准差
std_x = np.std(x, axis=0)
#z-score标准化
for i in range(len(x)):
    for j in range(len(x[0])):
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

5.5 读取测试数据.csv文件

训练数据和测试数据文件均为.csv且格式类似，方法类比读取训练数据即可：

#读取数据csv文件，data类型为矩阵
data = pd.read_csv("test.csv")
#数据切片
data = data.iloc[:, 2:]
#为了数学运算方便，将FAINFULL为NR的值转换为0
data=data.replace(["NR",[0]])
#将data转换为numpy矩阵
arr_data = data.to_numpy()

5.6 整理测试数据

sample = np.empty([9*240,18])
for id in range(240):
    #使用transpose()转置数据矩阵
    sample[(id*9):(id+1)*9,:] = arr_data[18 * id : 18 * (id + 1), :].transpose()
#输入矩阵
x = np.empty([240,9],dtype=float)
#输出矩阵
y = np.empty([240,1],dtype=float)
#赋值
for i in range(240):
            #reshape将数据转变为一行
            x[i,:] = sample[(i*9):(i+1)*9,9].reshape(1, -1)
#每一个特征的平均值
mean_x = np.mean(x, axis=0)
#每一个特征的标准差
std_x = np.std(x, axis=0)
#z-score标准化
for i in range(len(x)):
    for j in range(len(x[0])):
        if std_x[j] != 0:
            x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]

5.7 计算预测值并输出

y矩阵就是我们的预测值，但是实验要求了输出.csv文件的格式要求，所以我们要为其增加表头并标明id的顺序：

#求出预测值
y=np.dot(x,w)+b
#整理输出内容
headers=['id','value']
data=[]
for i in range(240):
    row=[]
    row.append('id_'+str(i))
    if y[i][0]>=0:
        row.append(y[i][0])
    else:
        row.append(0)
    data.append(row)
#写入
with open ('model_B_output.csv','w',encoding='utf-8',newline='') as fp:
    #写
    writer =csv.writer(fp)
    #设置第一行标题头
    writer.writerow(headers)
    #将数据写入
    writer.writerows(data)

---

6 模型设计

6.1 模型A：单独考虑PM2.5一个特征

为了对比不同学习率下的拟合过程以及后续作图比较，我们定义一个learning_rate列表设置不同的学习率，为了更好地比较，共设置6个不同的学习率：

#学习率
learning_rate = [0.001,0.005,0.01,0.05,0.1,0.5,1]
#图表颜色
color_list=['red','green','blue','yellow','black','pink','purple']

另外我们需要提前定义好迭代次数和#adagrad初始系数，以及数据集的大小方便平均数的计算，加快程序运行时间：

#迭代次数
iter_time = 10000
#adagrad系数
eps = 0.0000001
#记下x的长度
x_len=len(x)

每一个学习率对应一次迭代过程，每一次新的迭代都需要初始化w和b，以及记录迭代次数的列表iter和记录损失函数值随迭代次数变化的列表loss_list。

迭代过程中会计算损失函数的微分，并采用梯度下降法修改b和w的值：

for k in range(len(learning_rate)):
    #记录开始时间
    start=time.time()
    #列表用于记录损失函数值随迭代次数变化过程
    iter=[]
    loss_list=[]
    #初始化权重w和偏移b  
    w = np.empty([9,1])
    for i in range(len(w)):
        w[i]=[1]
    b = 0
    #初始化adagrad参数
    w_adagrad = 0
    b_adagrad = 0
    #梯度下降法迭代
    for i in range(iter_time):
        #这里是loss function
        loss = np.sum(np.power(np.dot(x,w)+b-y,2))/(x_len)
        #每10次迭代存一次值
        if i % 10 == 0:
            iter.append(i)
            loss_list.append(loss)
        #求w梯度
        w_gradient= 2*np.dot(x.transpose(), np.dot(x,w)+b-y)/x_len
        w_adagrad += np.mean(w_gradient) ** 2
        #求b梯度
        b_gradient= 2*np.sum(np.dot(x,w)+b-y)/x_len
        b_adagrad += b_gradient ** 2
        #更新w
        w = w - learning_rate[k] * w_gradient / np.sqrt(w_adagrad + eps)
        #更新b
        b = b - learning_rate[k] * b_gradient / np.sqrt(b_adagrad + eps)
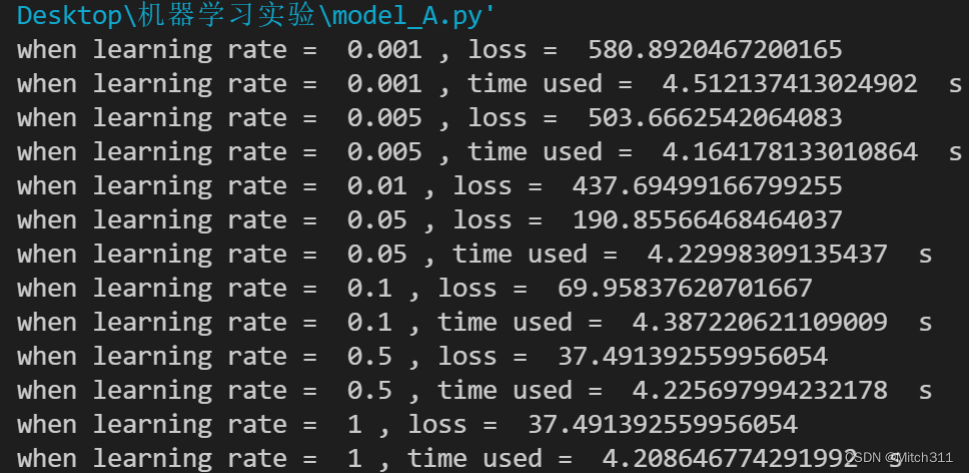
    print("when learning rate = ",learning_rate[k],", loss = ",loss)
    print("when learning rate = ",learning_rate[k],", time used = ",time.time()-start," s")
    plt.plot(iter, loss_list, c=color_list[k],label='learning_rate = '+str(learning_rate[k]))

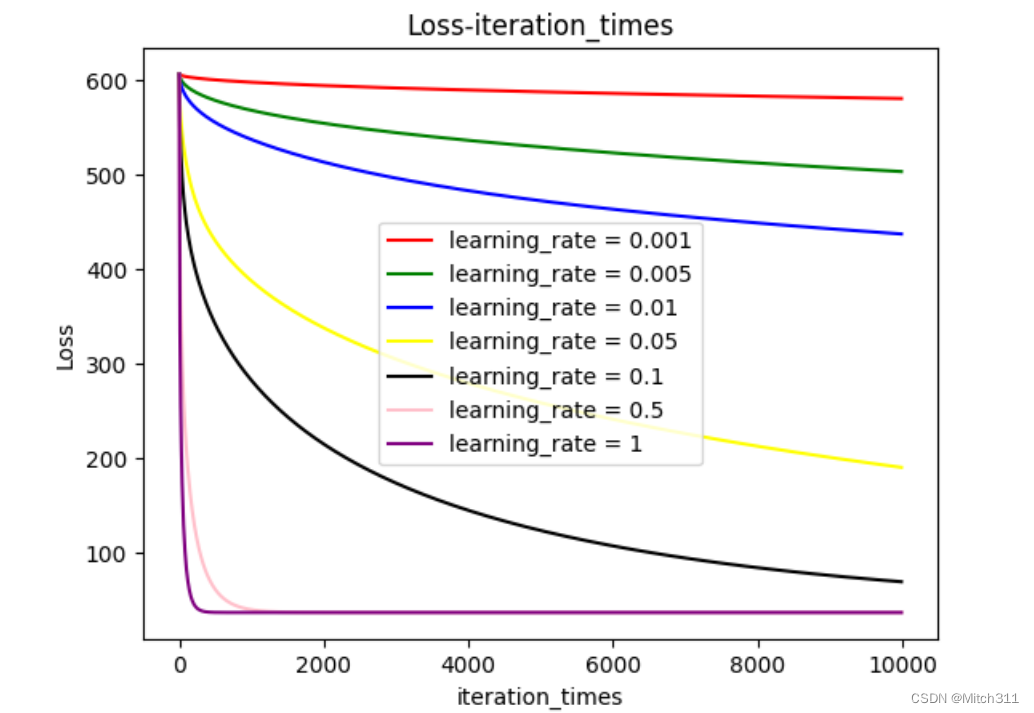
最后我们用图表来展示整个训练过程，loss随迭代次数的增加呈现出的变化过程：

#图表展示
plt.xlabel('iteration_times')
plt.ylabel('Loss')
plt.title('Loss-iteration_times')
plt.legend(loc='best')
plt.show()

6.2 模型B：考虑对PM2.5影响较大的七个特征

模型B不仅考虑pm2.5本身这个特征，额外考虑了几个对PM2.5影响较大的特征：NO₂、NO_x、O₃、PM10、降雨情况、RH。

因此模型的输入规模变化为12×471行/9×7列，数据提取时需要提取更多数据。

另外存储权重w的数组规模也随之变化为9×7行/1列。

其他的代码与模型A大同小异，具体详见附件中的源代码。

6.3 模型C：考虑数据集提供的所有十八个特征

模型C在模型B的基础上进一步发挥，综合全面运用所给的所有数据，考虑提供的所有特征值。

因此模型的输入规模变化为12×471行/9×18列，数据提取时需要提取更多数据。

另外存储权重w的数组规模也随之变化为9×18行/1列。

其他的代码与模型A大同小异，具体详见附件中的源代码。

---

7 实验结果

7.1 模型A：单独考虑PM2.5一个特征

7.1.1 loss值和运行时间

7.1.2 不同学习率下loss随迭代次数的变化情况

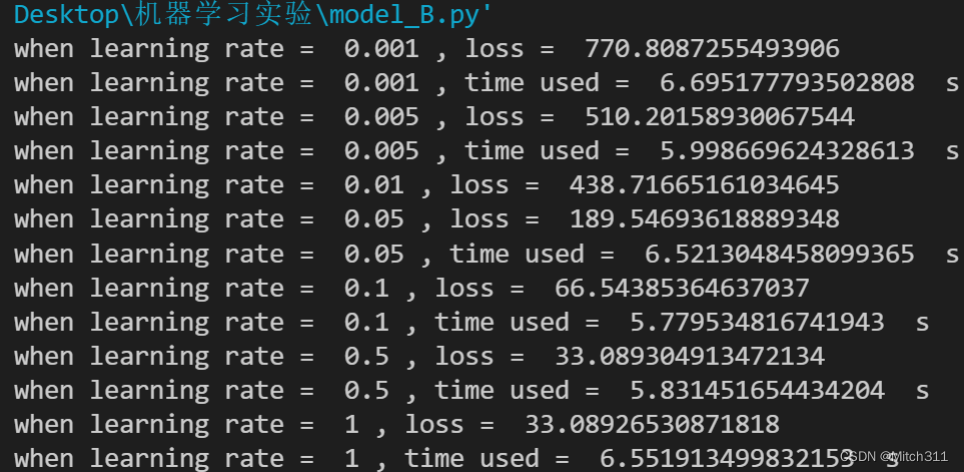
7.2 模型B：考虑对PM2.5影响较大的七个特征

7.2.1 loss值和运行时间

7.2.2 不同学习率下loss随迭代次数的变化情况

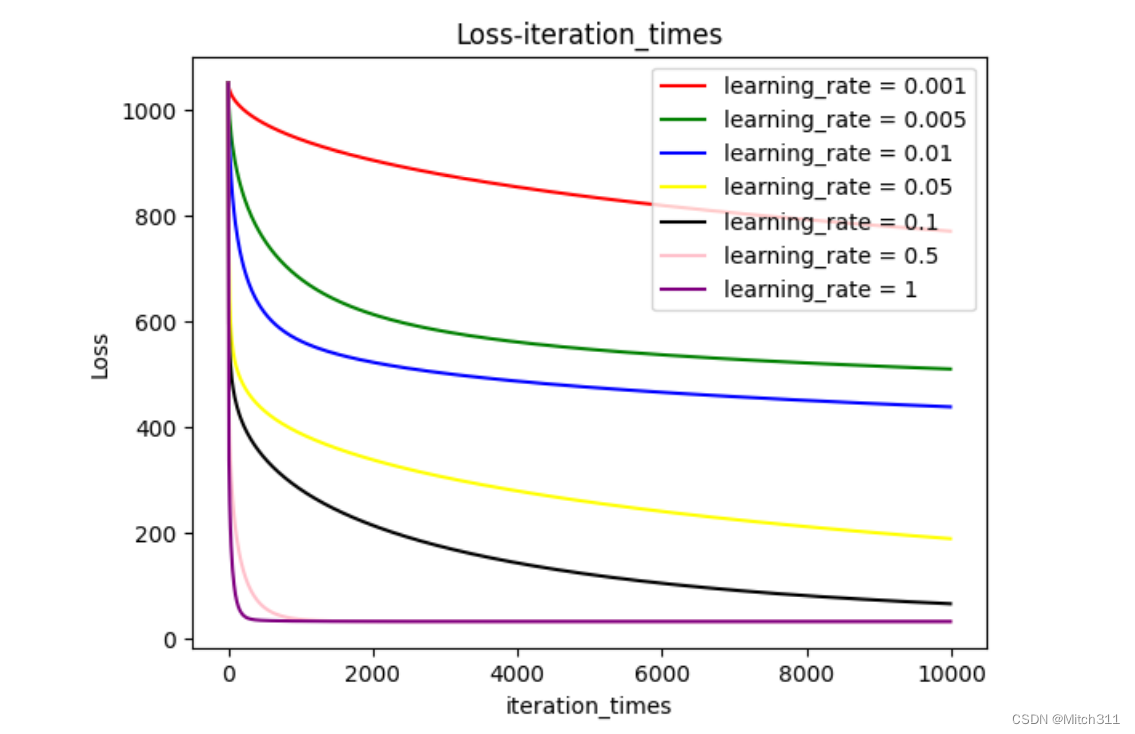
7.3 模型C：考虑数据集提供的所有十八个特征

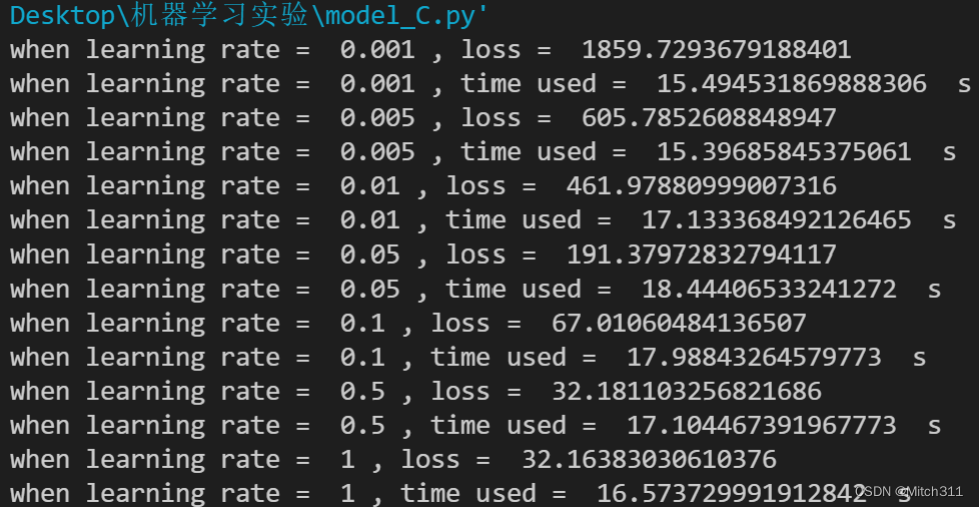
7.3.1 loss值和运行时间

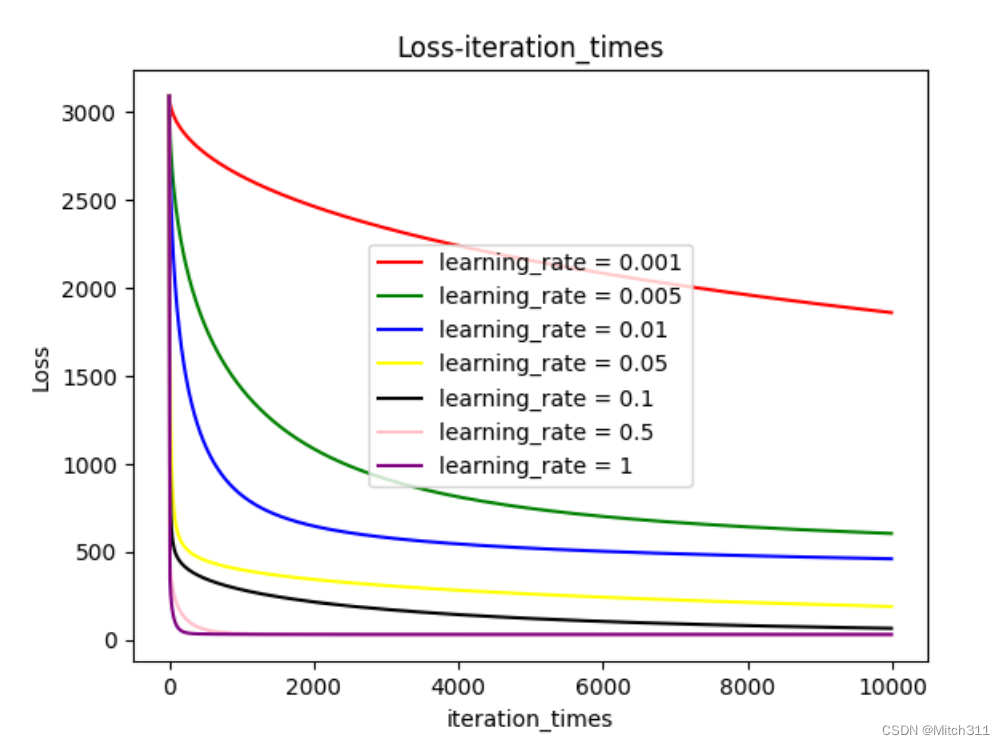
7.3.2 不同学习率下loss随迭代次数的变化情况

7.4 测试集的预测结果

使用三个模型分别预测了240笔testing data中的PM2.5值，见附件中的output.csv文件。

---

8 分析评估

8.1 不同模型对学习过程的影响

首先，比较三个模型的程序运行时间，模型A＜模型B＜模型C，原因显然是考虑的因素越多使用的资源就越多即运行时间越长，其中模型C的运行时间几乎是模型A和模型B的三倍之多。

其次比较三个模型在训练集上的表现，模型B和模型C比模型A略好，loss可以降得更低，但是差距不大，计算需要的时间稍长一点。

另外比较三个模型在测试集上的表现，模型B和模型C相比模型A同样更加出色，参见附件中的output文件，模型B和模型C在测试集上的输出更加合理，相比模型A的loss更小。

以上两个指标说明合理的测试模型能让机器学习的效果事半功倍，适当考虑一些对预测特征相关的因素可以让模型的拟合效果更好。

综上，个人认为模型B的性价比最高，因为考虑的特征更少，运行时间更短，并且在训练集和测试集上的表现都和C几乎一样，相比之下C消耗的资源显然是更多的。

8.2 不同学习率对学习过程的影响

一共测试了6种不同学习率下loss随迭代次数增加的变化过程，三种模型在图像上描绘出来的结果主要不同在于loss值的大小，但是整个变化过程大同小异。

和预想的一致，更高的学习率意味着更快的收敛，学习率越高收敛越快，学习率越低收敛越慢，而且如果学习率过小甚至无法在规定的迭代次数内呈现出收敛趋势。

另外，收敛线对应loss值的大小也不一样，学习率高的模型收敛时loss更小，学习率低的模型收敛时loss更大。

分析原因是由于使用了Adagrad算法，如果初始设置的学习率过小，随着迭代次数增加，学习率越来越小，很有可能在没有到达极值点的时候就处于停滞不前的状态。

---

9 References

[1] python.org

[2] kaggle.com

[3] 百度百科

[4] CSDN专业开发者技术社区

[5] 十分钟入门 Pandas | Pandas 中文 (pypandas.cn)