给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

• 节点的左子树只包含 小于 当前节点的数。
• 节点的右子树只包含 大于 当前节点的数。
• 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

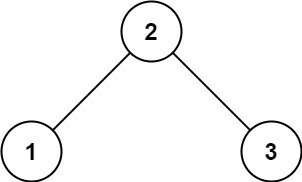
输入：root = [2,1,3]
输出：true

示例 2：

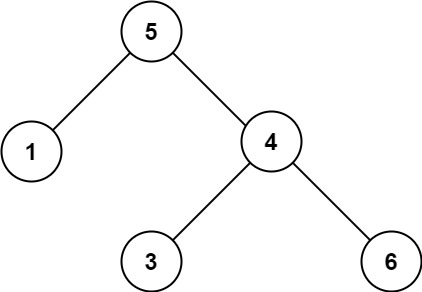
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：

• 树中节点数目范围在[1, 104] 内
• -231 <= Node.val <= 231 - 1

该二叉树符合中序遍历的思想，所以利用中序遍历的代码模式进行递归就可以结题

回顾中序遍历的递归代码:

        中序遍历是二叉树的一种遍历方式，它先遍历左子树，再遍历根节点，最后遍历右子树。而我们二叉搜索树保证了左子树的节点的值均小于根节点的值，根节点的值均小于右子树的值，因此中序遍历以后得到的序列一定是升序序列

    private void inorderHelper(TreeNode root, List<Integer> result) {
        if(root == null) return;
        inorderHelper(root.left, result); // 递归遍历左子树
        result.add(root.val); // 访问根节点
        inorderHelper(root.right, result); // 递归遍历右子树
  }

本题目的思路：
1、要满足两边子树也都是二叉搜索树【即中序遍历前数小于后数】

2、中序遍历代码改为如下所示：

3、前书用一个变量“pre”，将中序遍历的中间步骤换成pre的赋值

        boolean l=isValidBST(root.left);
        if(root.val<=min)   return false;
        min=root.val;
        boolean r=isValidBST(root.right);

 

代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
            
    long min=-Long.MIN_VALUE;// 记录上一个节点的值，初始值为int的最小值

    public boolean isValidBST(TreeNode root) {

        if(root==null){
            return true;
        }
        boolean l=isValidBST(root.left);
        if(root.val<=min){
            return false;
        }
        else{
            min=root.val;
        }
        boolean r=isValidBST(root.right);

        return r&&l;

    }
}