目录
一、查找的基本概念
二、顺序查找
关键代码
完整代码
运行结果
增加哨兵
三、二分查找(折半查找)
关键代码
完整代码
运行结果
四、分块查找
图示
关键代码
完整代码
一、查找的基本概念
- 对查找表进行的操作
1.查找某个特定的数据元素是否存在
2.检索某个特定数据元素的属性
3.在查找表中插入一个数据元素
4.在查找表中删除一个数据元素 - 静态查找(Static Search Table)——在查找过程中仅查找某个特定元素是否存在或它的属性的,称为静态查找。
- 动态查找(Dynamic Search Table)——在查找过程中对查找表进行插入元素或删除元素操作的,称为动态查找。
- 关键字(Key)——数据元素(或记录)中某个数据项的值,用它可以标识数据元素(或记录)。
- 主关键字(Primary Key)——可以唯一地标识一个记录的关键字称为主关键字。
- 次关键字(Secondary Key)——可以标识若干个记录的关键字称为次关键字。
- 查找(Searching)——在查找表中确定是否存在一个数据元素的关键字等于给定值的操作,称为查找(也称为检索)。若表中存在这样一个数据元素(或记录),则查找成功;否则,查找失败。
- 内查找和外查找——若整个查找过程全部在内存进行,则称为内查找;若在查找过程中还需要访问外存,则称为外查找。
- 平均查找长度ASL——查找算法的效率,主要是看要查找的值与关键字的比较次数,通常用平均查找长度来衡量。
二、顺序查找
- 顺序查找,也称线性查找,通常用于线性表。
- 算法思想:从头到尾挨个找
-
关键代码
int Search_Seq(SSTable S, ElemType key)
{
for (int i = 0; i < S.len ; i++)
{
if (S.elem[i] == key)
return i;//查找成功,返回元素下标
}
return -1;
}-
完整代码
#include<iostream>
#include<stdio.h>
#include<malloc.h>
#include<iomanip>
using namespace std;
typedef int ElemType;
typedef struct
{
ElemType* elem;//动态数组基址
int len;//表的长度
}SSTable;
int Search_Seq(SSTable S, ElemType key)
{
for (int i = 0; i < S.len ; i++)
{
if (S.elem[i] == key)
return i;//查找成功,返回元素下标
}
return -1;
}
int main()
{
SSTable s;
s.elem = (int*)malloc((80*sizeof(int)));
s.len = 0;
for (int i = 0; i <80 ; i++)
{
s.elem[i] = (rand() % 150 + 1);//产生【1,150】之间任意的随机整数
s.len++;
}
int key;
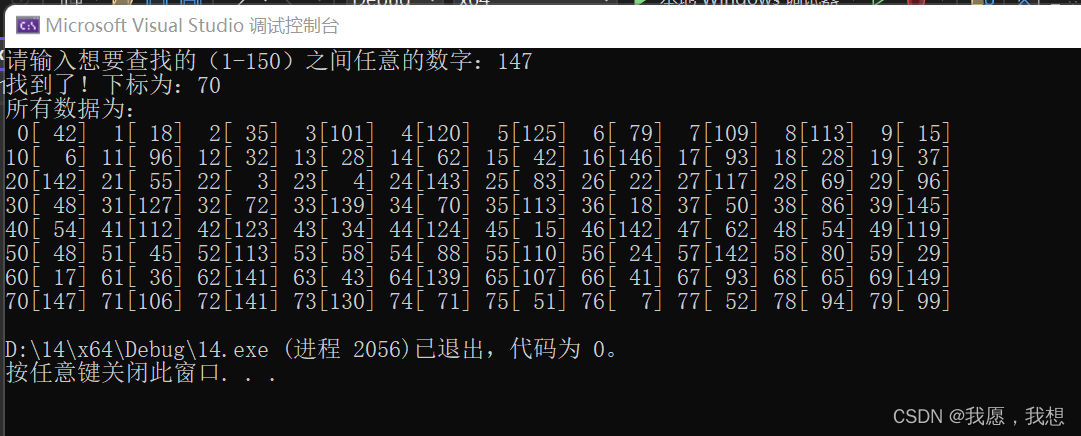
cout << "请输入想要查找的(1-150)之间任意的数字:";
cin >> key;
if (Search_Seq(s, key) != -1)
{
cout << "找到了!下标为:" << Search_Seq(s, key)<<endl;
}
else
cout << "未找到!" << endl;
cout << "所有数据为:" << endl;
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 10; j++)
{
cout << setw(2) << 10 * i + j << "[" <<setw(3)<< s.elem[10 * i + j] << "]" << " ";
//setw()函数使输出对齐
}
cout << endl;
}
return 0;
}-
运行结果
-
增加哨兵
int Search_Seq(SSTable S, ElemType key)
{
S.elem[0] = key;//S.elem[0]称为监视哨,可以起到防止越界的作用。
int i = S.len;
while (S.elem[i] != key)//从后往前找
{
i--;
}
return i;//查找成功返回元素下标,查找失败返回0
}三、二分查找(折半查找)
- 基本思路:在有序表中,取中间元素作为比较对象,若给定值与中间元素的关键字相等,则查找成功;若给定值小于中间元素的关键字,则在中间元素的左半区继续查找;若给定值大于中间元素的关键字,则在中间元素的右半区继续查找。不断重复上述查找过程,直到查找成功,或所查找的区域无数据元素,查找失败。
-
关键代码
int BinSearch(int* data,int n, int key)//折半查找
{
int low = 0, high = n - 1;
int mid = 0;
while (low <= high)
{
mid = (low + high) / 2;
if (key < data[mid])//继续在data[low,mid-1]左区间查找
high = mid - 1;
else if (key > data[mid])//继续在data[mid+1,high]右区间查找
low = mid + 1;
else
return mid;//查找成功
}
return -1;//查找失败,返回-1
}-
完整代码
#include<iostream>
#include<stdio.h>
#include<algorithm>//sort函数的头文件
#include<iomanip>//setw()函数的头文件
using namespace std;
int BinSearch(int* data,int n, int key)//折半查找
{
int low = 0, high = n - 1;
int mid = 0;
while (low <= high)
{
mid = (low + high) / 2;
if (key < data[mid])//继续在data[low,mid-1]左区间查找
high = mid - 1;
else if (key > data[mid])//继续在data[mid+1,high]右区间查找
low = mid + 1;
else
return mid;//查找成功
}
return -1;//查找失败,返回-1
}
int main()
{
int a[80] = { 0 };
for (int i = 0; i < 80; i++)
{
a[i] = (rand() % 200 + 1);//产生【1,200】之间任意随机数
}
sort(a, a + 80,less<int>());//使用现成的sort函数,从小到大排序
//sort(a, a + 80, greater<int>());//从大到小排序
int key;
cout << "请输入(1-200)之间想要查找的数字:";
cin >> key;
if (BinSearch(a, 80, key) != -1)
{
cout << "查找成功!" << "下标为:" << BinSearch(a, 80, key) << endl;
}
else
{
cout << "查找失败!" << endl;
}
cout << "所有数据是:" << endl;
for (int i = 0; i < 8; i++)
{
for (int j = 0; j < 10; j++)
{
cout << setw(2) << 10 * i + j << "[" << setw(3) << a[10 * i + j] << "]" << " ";
}
cout << endl;
}
}-
运行结果

四、分块查找
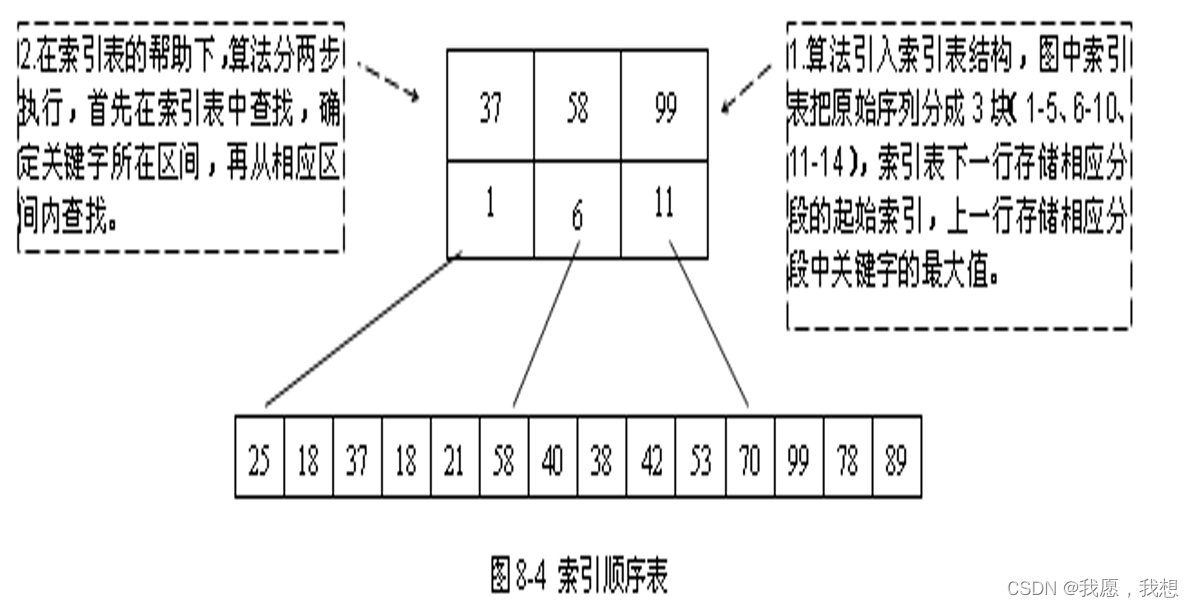
- 分块存储的索引表中保存的是各个分块的最大的元素和分块的存储区间
- 特点:块内无序、块间有序
- 算法过程:
1.在索引表中确定待查记录所属分块
2.在块内顺序查找 -
图示
-
关键代码
int IdxSearch(int*data, Index I[], ElemType key,int n,int b)
//分块查找key,索引表为I[0,..,b-1]
{
int s=n/b;//索引表内每块元素个数
int low = 0, high = b - 1;
int mid = 0;
while (low <= high)//在索引表中折半查找
{
mid = (low + high) / 2;
if (key <= I[mid].maxkey)
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}
if (low <= b - 1)
{
for (int i = I[low].link; i <= I[low].link+s-1&&i<n; i++)//在数组中顺序查找
{
if (key == data[i])
return i;
}
return 0;
}
}-
完整代码
#include<iostream>
#include<stdio.h>
using namespace std;
//#define b 6;//索引表的最大长度
typedef int ElemType;
typedef struct//索引表
{
ElemType maxkey;
int link;//分块区间的起始下标
}Index;
int Max(int& a, int& b)
{
if (a <= b)
return b;
else
return a;
}
void Init(int* data, Index I[], int n, int b)//初始化索引表
//索引表为I[0, .., b - 1]
{
int max = 0;
int s = n / b;
for (int i = 0; i <=b-1; i++)//初始I[i]分块
{
for (int j = i * s; j <= s * (i + 1) - 1; j++)
{
max = Max(max, data[j]);
}
I[i].maxkey = max;
I[i].link = i * s;
}
}
int IdxSearch(int*data, Index I[], ElemType key,int n,int b)
//分块查找key,索引表为I[0,..,b-1]
{
int s=n/b;//索引表内每块元素个数
int low = 0, high = b - 1;
int mid = 0;
while (low <= high)//在索引表中折半查找
{
mid = (low + high) / 2;
if (key <= I[mid].maxkey)
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}
if (low <= b - 1)
{
for (int i = I[low].link; i <= I[low].link+s-1&&i<n; i++)//在数组中顺序查找
{
if (key == data[i])
return i;
}
return 0;
}
}
int main()
{
int a[] = { 8,14,6,9,10,22,34,18,19,31,40,38,54,66,46 };
int size = sizeof(a) / sizeof(a[0]);//数组a中元素个数
Index I[3];
Init(a, I, size, 3);
int x;
cout << "请输入想要查找的元素:";
cin >> x;
cout<<"下标为:"<<IdxSearch(a, I, x, size, 3);
return 0;
}