期末考核方式

• 微分方程的两种解：解析解和数值解。
• 期末考试，会有一个大题，两小问：给你一阶常微分方程，要么是变量可分离的形式，要么是一阶线性形式。第一小问，会要求求解析解，第二小问会使用数值解。
• 解析解：要求使用的分离变量法或者积分因子法
• 数值解：显示欧拉、隐式欧拉、改进欧拉，三种都考

基础知识

• 微分方程：方程中为未知数的导数

• 常微分方程：方程中仅仅只有一个未知数

• 偏微分方程：方程中有多个未知数

• 阶数：方程中未知数导数的最高阶

• 初边值条件：求微分的过程中，需要知道常数信息，才能唯一确定方程的解。
  

• 如果是自己针对实际问题建立微分模型，不要着急求解，需要先判定合理性。在物理上判定模型的建立过程是否符合客观定律，从数学的角度看，方程是否是适定的。

• 适定性：

  • 连续依赖定解条件，用来定界的初边值条件误差足够小，你解出来的最终解误差就可以足够小。
  • 解存在且唯一

• L：近似为f（x，y）对y的一阶偏导的绝对值。

• 求解方式
  

• 解析解：一般是最好的解决方式的，但是一般解不出来。

• 数值解：未知函数，在足够多点上，足够高精度的近似。

解析解（公式法）

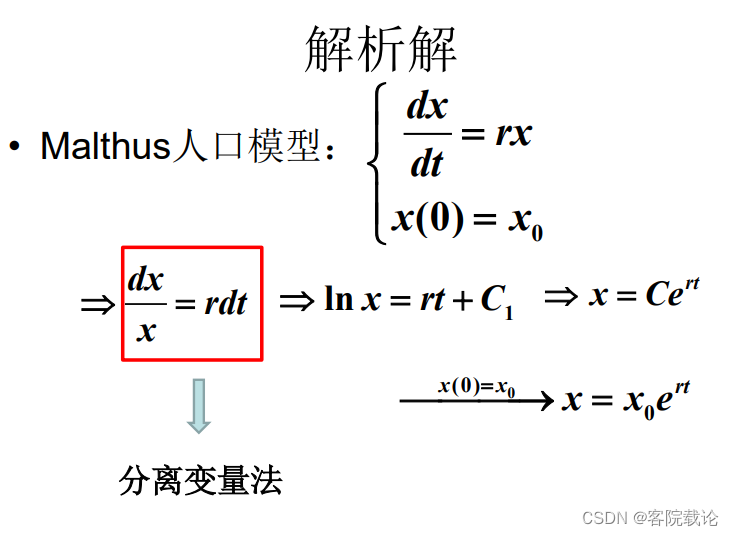
• 条件：f（x，y）是一个变量可分离的形式，将一阶常微分转变为两个不定积分。

• 为了实现整体的协调性，这里将r替换为单调递减的函数，来控制变量的增加。
• f（x，y）要是变量可分离的形式，将微分方程写成两个解析解。
  
• 公式法，任何一个一阶线性都可以使用公式法进行求解。转化之后的不定积分要会积分。
  
  
• 变量可分离，转化为的两个不定积分，然后转化之后的不定积分可以求解。

解析解例题（使用公式法，必考）

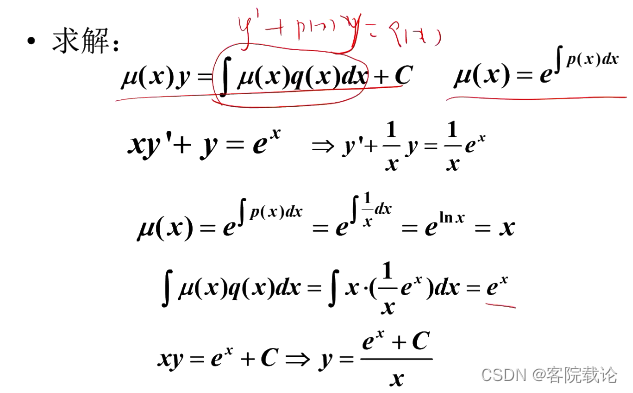
• 注意，这里先微分方程化成一般的形式，然后求取对应μ（x）

解析解的局限性

• 数值解是求取目标函在某些点上十分精确的近似。

数值解

数值解的基本流程

• 网格剖分，最好的情况是使用自适应的方法解决，过于复杂，不作为本课程的研究内容。默认是使用均匀划分进行解决
• 离散：根据之前网格剖分获得的点，带入微分方程，生成新的代数方程
• 求解：求解对应的代数方程，重在于表示离散点的导数关系。
  

显示Euler法

显示欧拉（差值理解）

• 显式：右侧使用的条件都是已知的
• 向前：计算Xk的时候，使用了Xk+1的值
• 这里始终是近似，并不是真实值。

显示欧拉（Taylor展开理解）

• 做泰勒展开，只展开到线性项，将高阶导数丢弃。

显示欧拉（数值积分法理解）

• 先对原来的方程做定积分
  
• 使用左矩形公式计算定积分

几何意义

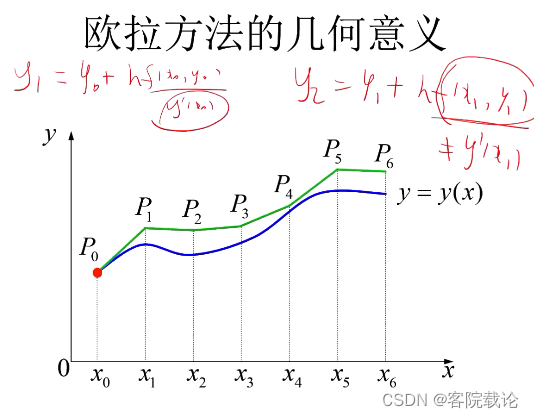
• 欧拉折线法，使用折线近似原始的函数。
• 任何一个一阶常微分方程都可以使用显示欧拉进行计算。

显示欧拉法例题（必考）

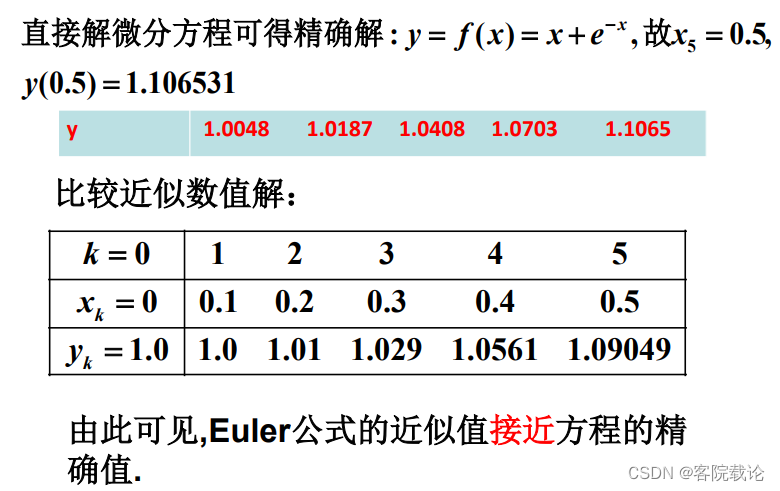
隐式Euler

• 向后欧拉，通过向后找前面的点。需要解方程，才能获得下一次迭代的点。
• 这里不同于显示欧拉，主要是通过差分近似的是前面一个点还是后面一个点。
  
• 如果你的隐式欧拉方程解的是非线性，就需要使用不动点迭代。
  
• 不动点迭代未必收敛，需要关心不动点迭代收敛的条件。
• 一般来说，隐式欧拉更加准确。
  
• 没听懂，不会考，会做题就行。
• 左矩形得到显式欧拉，右矩形得到隐式欧拉。

使用梯形公式的隐式欧拉

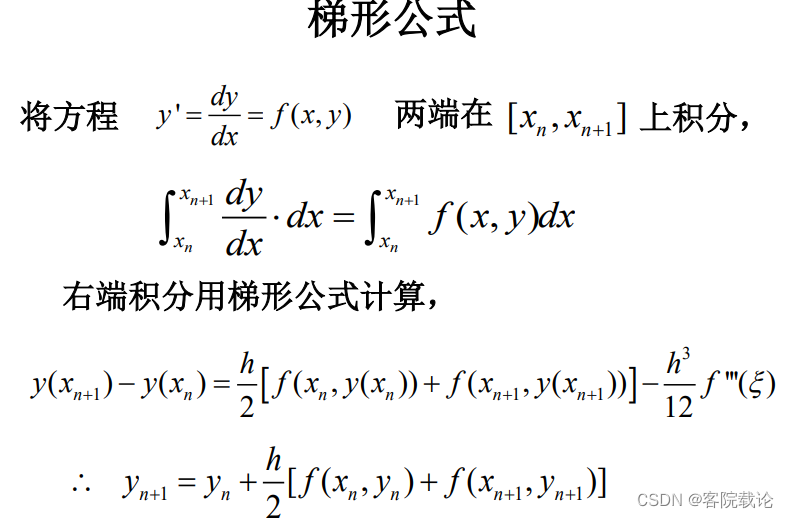
改进Euler（欧拉预估校正公式）（必考）

• 已经讲了三个格式：显示欧拉，隐式欧拉，梯形公式
• 先使用显示欧拉，预估一次，然后在使用梯形公式进行矫正，然后迭代一次即为最终的结果。
• 改进欧拉是显格式
  

改进欧拉的计算例题（必考）

• 需要写好公式，然后在逐个代入计算

误差（了解）

整体截断误差Error

• 很难分析，因为计算不出来实际值，所以一般使用局部截断误差进行估计。
• 整体截断误差：前一步产生的误差+当前近似计算产生的误差

局部截断误差Trunction Error

• 局部截断误差比整体截断误差更容易分析，可以用来参考，用来分析整体截断误差。真是需要的是整体截断误差，但是实际计算中使用的是局部截断误差。
• 整体截断误差比局部截断误差更大，局部截断误差是建立在之前都是正确的情况下，进行分析的。

• 注意：P+1次方，是P阶算法

局部截断误差分析

• 隐式和显示都是一阶方法，梯形和改进都是二阶方法。

R-K方法（不考，就没记）

总结