回归

简单模型的梯度计算

最简单的线性模型可以简化为y=wx,x是输入，w是参数，是模型需要计算出来的，y是预测值，*可以看成网络中的计算。

其实这就可以是一个简单的神经元模型。w需要不断更新：计算损失函数loss对w的导数


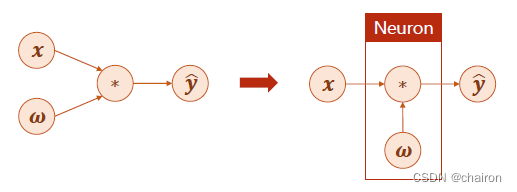
那么对于复杂的神经网络该怎么样进行梯度计算，进行参数的更新呢?

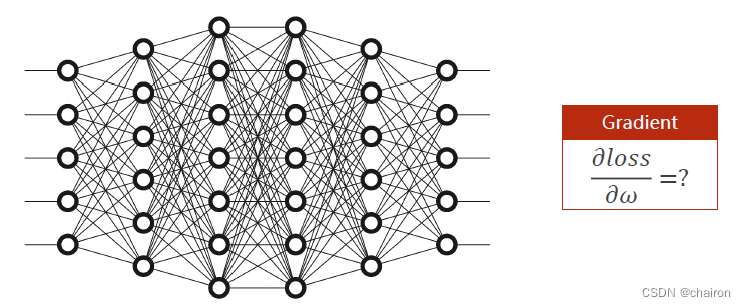
分析：假设输入x1~x5，经过多层神经元最后得到y1-y5。每个神经元都有一个权重w需要计算，如何计算损失函数对每一个输入的微分呢？
如果按照之前的梯度下降，根据链式求导法则，那么需要计算的微分公式非常长，计算非常复杂。

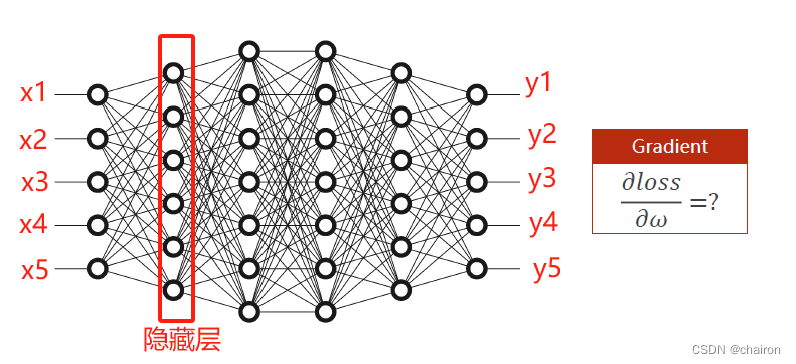
那么有没有一种方式能够比较方便的计算这种复杂的神经网络的梯度呢？
反向传播！

反向传播

计算图

一个神经元：输入X和权重W先进行矩阵乘法，再进行矩阵加法。（所有输入、输出、参数都是向量或者矩阵）

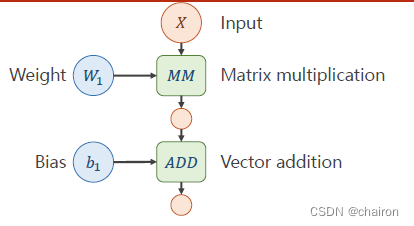
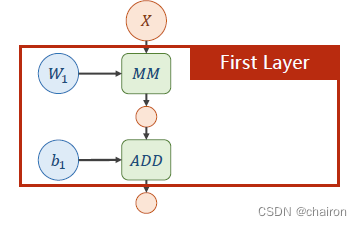
图中绿色部分表示运算：
MM：矩阵乘法，ADD：加法。
两种运算的求导方法不一样哟！

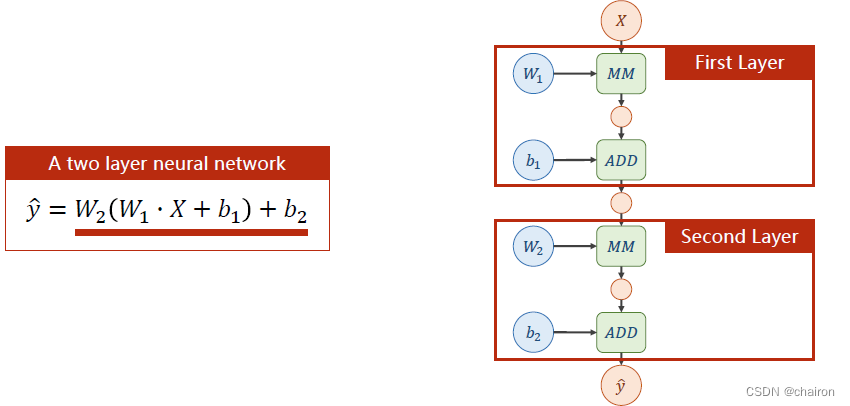
对这两层神经元计算公式进行展开，我们会发现：不管有多少层神经元，最终都可以表示成一个形式：$WX+B$。这个计算式是可以展开的，这样计算量是完全没有变化的！

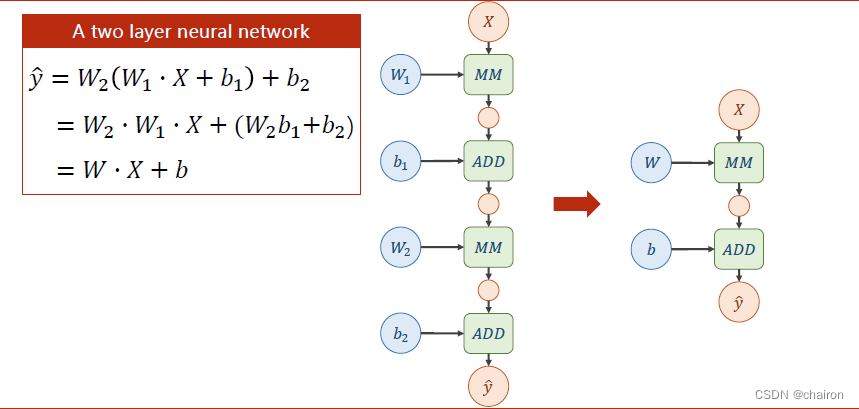
于是！我们可以在每层神经元之后加一个非线性激活函数！比如说Sigmoid函数，这样函数就没法再展开了。

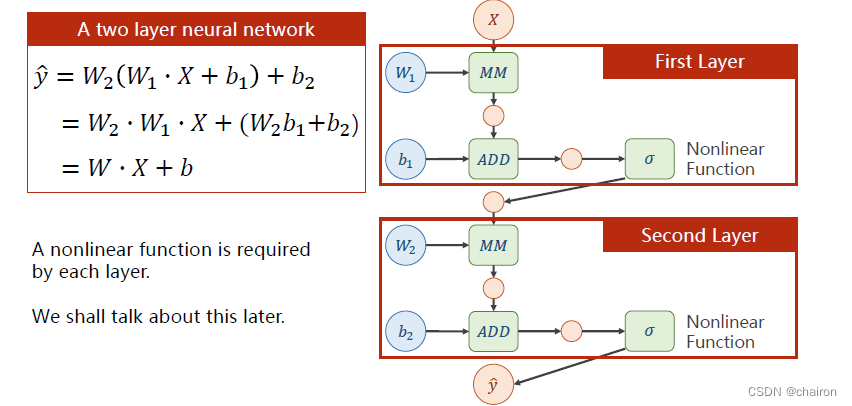
链式求导

链式法则定理：

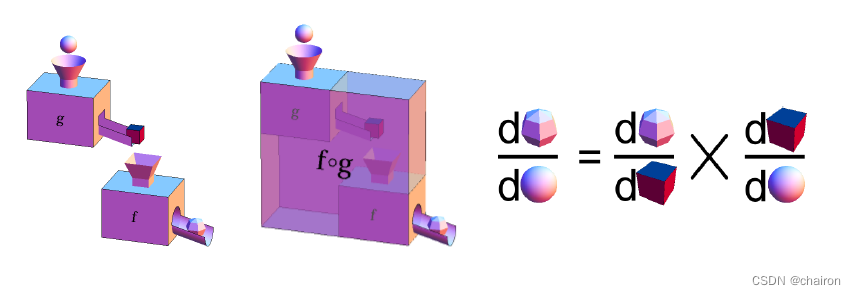
假如 y = f (u)是一个u的可微函数，u = g (x)是一个x 的可微函数，则 y = f (g(x)) 是一个x 的可微函数，并且：

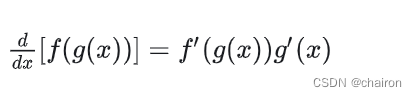
即y 对x 的导数，等于y 对u 的导数，乘以u 对x 的导数。
或者，写成等价形式：

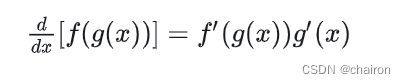
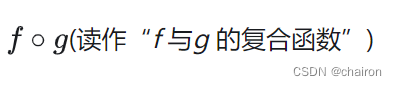
Forward 前馈计算

Forward 前馈计算：就是从输入x一步步往后计算$Z=f(x,w)$，得到最后Loss的过程。

• 在这个过程中能够很容易计算出Z对x、w的偏导数。
  
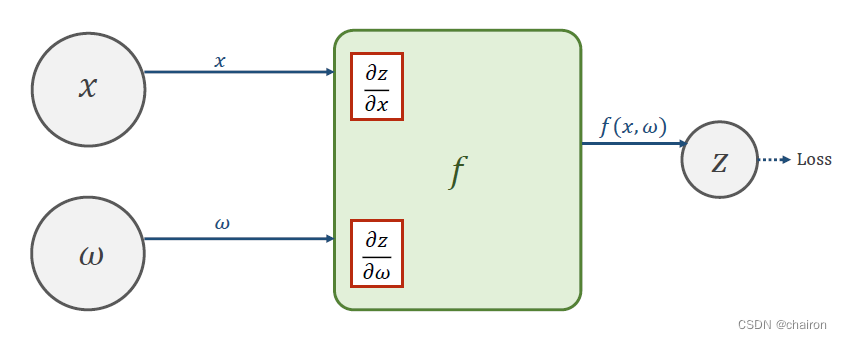
  求得Loss以后，就可以很容易得到Loss对Z偏的导数：
  

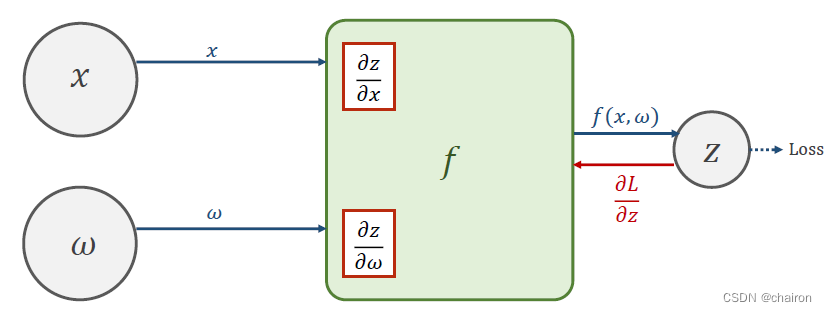
反向传播Back Propagation

然后就可以反向利用链式求导法则计算：Loss对x、w的偏导数（我们最终要求的结果！这就是更新阐述w所需要的梯度）这就是反向传播！

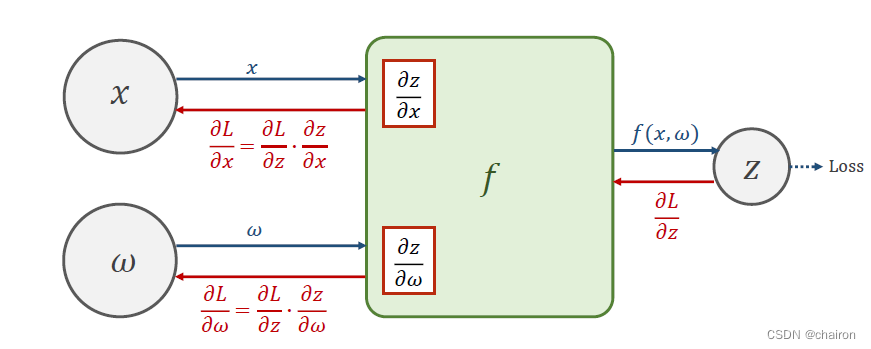
其实这个Back Propagation 过程就算一个逆向的Forward过程。

例子

假设：𝑓 = 𝑥 ∙ 𝜔, 𝑥 = 2, 𝜔 = 3
前馈过如下，一层层计算最后可以得到Z，然后计算出Loss。

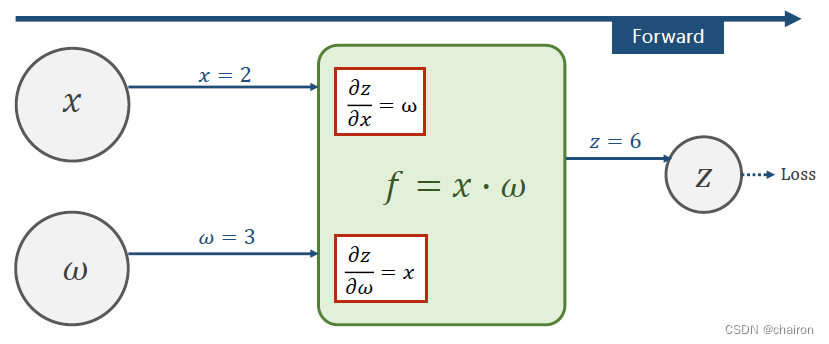
假设Loss对Z的偏导数为5（可以根据损失函数计算出来），反向传播过程计算如下：

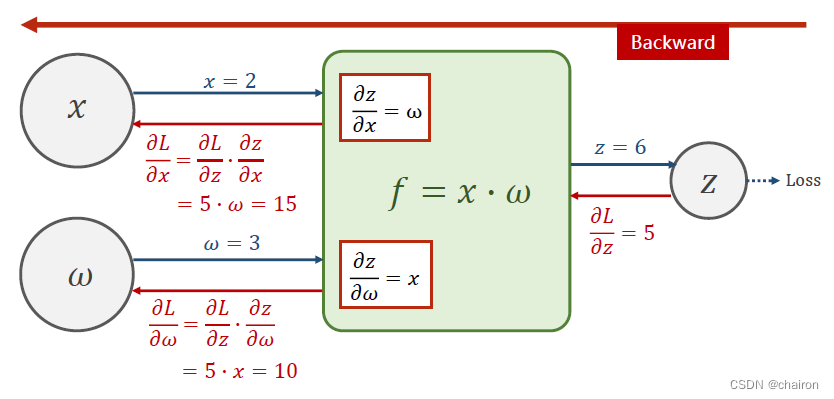
反向传播的目的是进行梯度计算，即：计算Loss对w的偏微分

线性模型的计算图计算

前馈过程

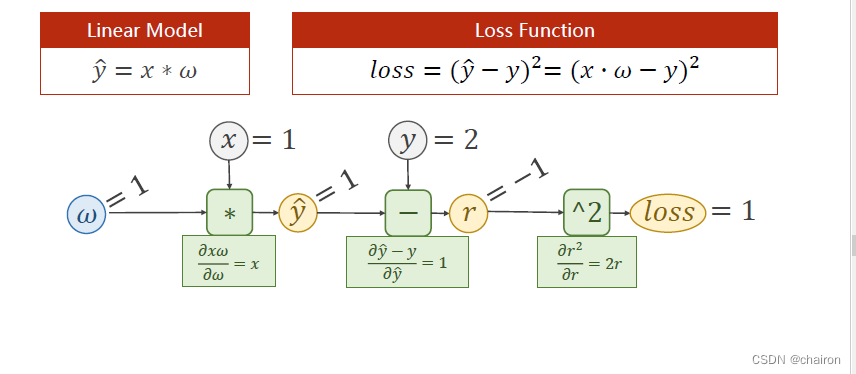
已知：x=1，y=2；设置w的初始值为1.
则：y_hat=1,y_hat-y=1,loss=1
则：可以求出y_hat 对 w的偏导数：x=1；r=y_hat-y,求出r对y_hat的偏导数：1；求出loss对r的偏导数：2r=-2

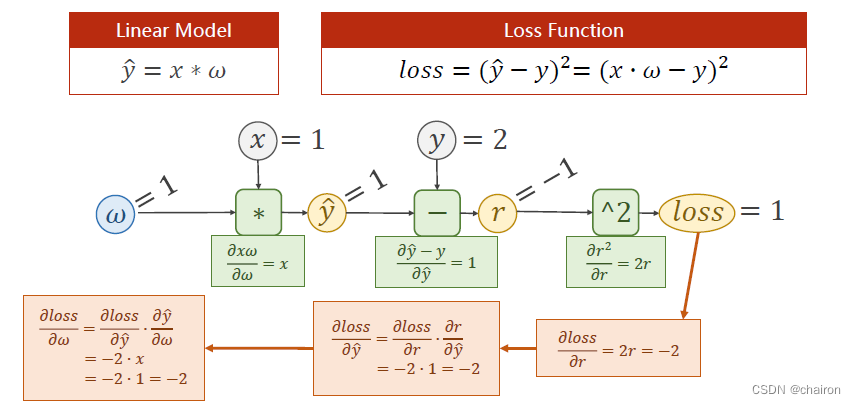
反向传播过程（逆向求导）

已知：loss对r的偏导数：-2 、r对y_hat偏导数：1、y_hat对w偏导数：1
求得：loss对w的偏导数：根据链式求导法则，相乘就可以得到啦！

练习

1. 假设：𝑓 = 𝑥 ∙ 𝜔, 𝑥 = 2, 𝜔 = 1，
   请根据上述计算图的过程，计算出梯度（loss对w的偏微分）
   
2. 假设：𝑓 = 𝑥 ∗ 𝜔 + 𝑏,𝑥 = 1, 𝜔 = 1，𝑏=2
   请根据上述计算图的过程，计算出梯度（loss对w、b的偏微分）
   
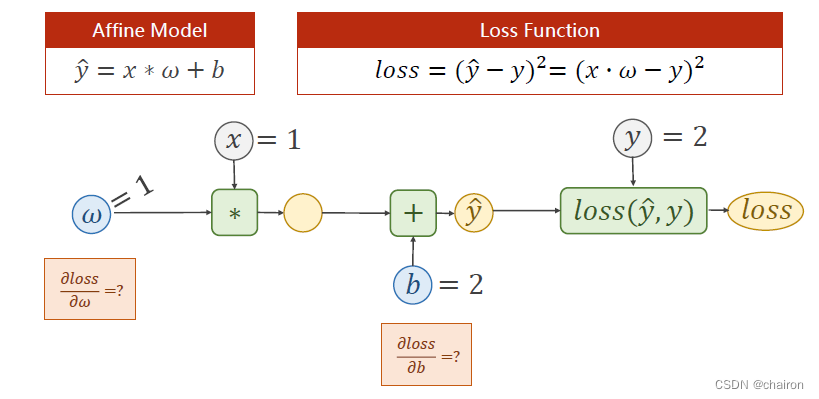
   丑丑的计算过程：
   

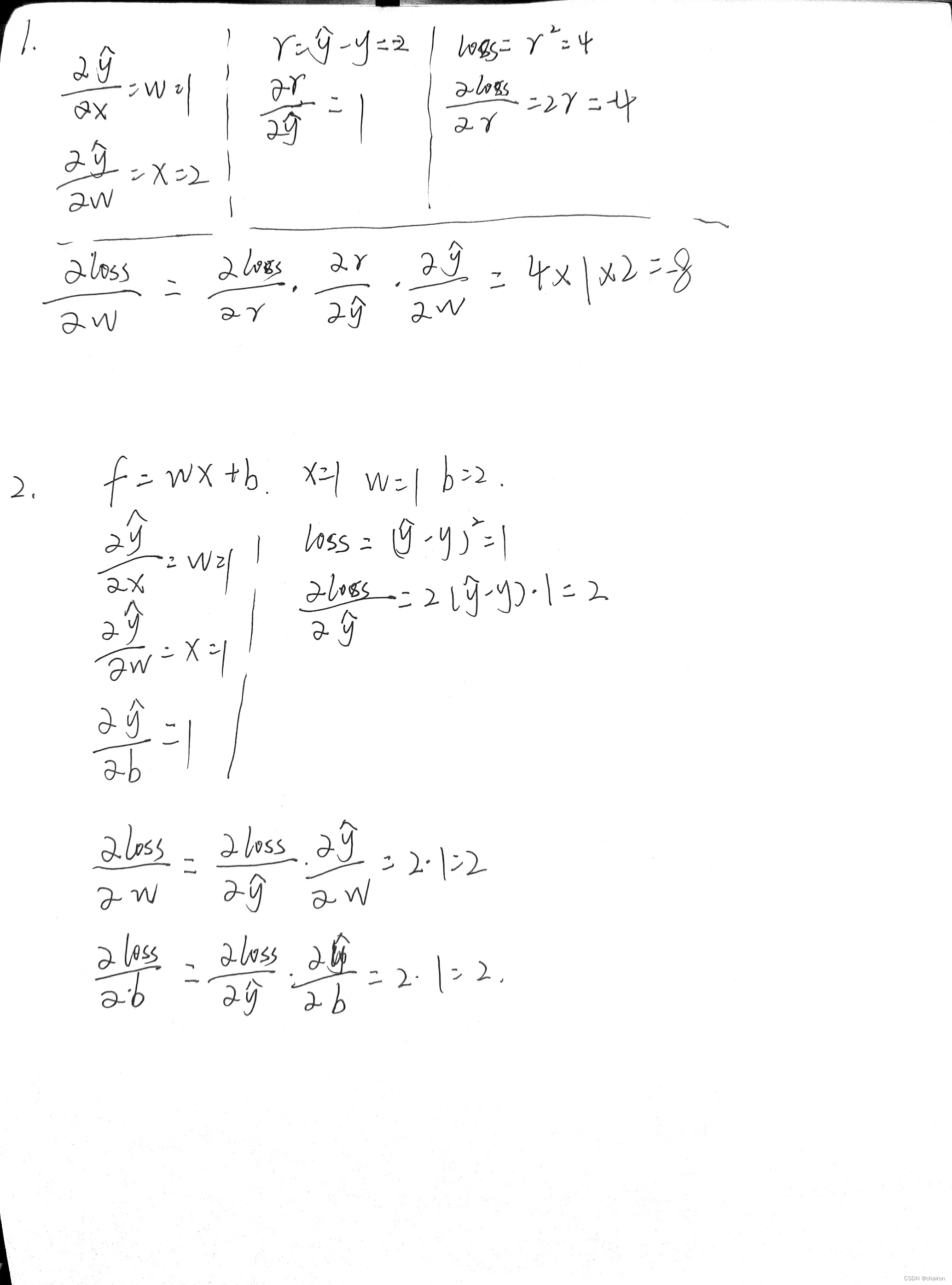
Pytorch中的前馈过程和反向传播过程

Tensor

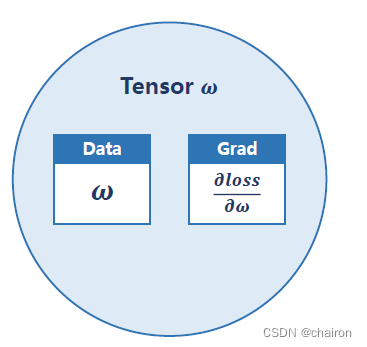
Tensor（张量）：可以是标量、向量、矩阵、多维向量… 包含两个属性：

• data:存储参数w数据
• grad:存储梯度：loss对w的偏导数