【POJ No. 1988】 方块栈 Cube Stacking

POJ 题目地址

【题意】

贝西正在玩方块游戏，方块编号为1～N（1≤N ≤30,000），开始时每个方块都相当于一个栈。

贝西执行P 个（1≤P ≤100,000）操作，操作类型有两种：M X Y ，将包含X 的栈整体移动到包含Y 的栈顶部；C X ，查询X 方块下的方块数量。请统计贝西每个操作的结果。

【输入输出】

输入：

第1行为单个整数P ，表示操作的数量。第2～P +1行：每一行都描述一个操作（注意：N 的值不会出现在输入文件中，没有一种移动操作会请求将栈移动到自身）。

输出：

对每个C操作，都输出统计结果。

【样例】

【思路分析】

这道题包括移动和计数两种操作，方块的整体移动可以使用二维数组实现，但是操作数量很大，若一个一个地移动，则会超时。

整体移动相当于集合的合并，因此可以借助并查集实现，在集合查找和合并时，更新树根下方的方块数量即可。使用并查集可以快速、高效地解决该问题。

【算法设计】

① 初始化。初始化每个方块的集合号都为其自身。

② 查询或者合并。

• C X ：查询X 的集合号，并输出X 方块下的方块数量。d [i ]表示第i 个方块下的方块数量。查询X 的祖宗，在返回过程中将经过路径上节点的集合号统一为祖宗的集合号，将当前节点的d 值加上其父节点的d 值。
• M X Y ：合并X 、Y 集合号。cnt[i ]表示第i 个栈的方块数量。首先找到X 、Y 所在的集合祖宗a 、b ，然后将a 的集合号修改为b ，fa[a ]=b ，更新d [a ]=cnt[b ]，cnt[b ]+=cnt[a ]。

【举个栗子】

① 初始化。根据输入样例，初始时每个方块的集合号都为其自身，fa[i ]=i ；在每个方块下都有0个方块，d [i ]=0；每个栈只有1个方块，cnt[i ]=1。

② 合并。M 1 6：将包含1的栈整体移动到包含6的栈。首先找到1和6的祖宗1、6，然后将1的集合号修改为6，fa[1]=6，更新d[1]=cnt[6]=1，cnt[6]+=cnt[1]=2。

③ 查询。C 1：查询1下面有多少个方块。首先查询1的集合号，找祖宗，在查询过程中将当前节点的d 值加上其父节点的d 值，d[1]+=d [6]=1。

④ 合并。M 2 4：将包含2的栈整体移动到包含4的栈。首先找到2和4的祖宗2、4，然后将2的集合号修改为4，fa[2]=4，更新d[2]=cnt[4]=1，cnt[4]+=cnt[2]=2。

⑤ 合并。M 2 6：将包含2的栈整体移动到包含6的栈。首先找到2和6的祖宗4、6，然后将4的集合号修改为6，fa[4]=6，更新d[4]=cnt[6]=2，cnt[6]+=cnt[4]=4

注意：只修改祖宗集合号，2号方块的集合号及d 值并没有修改，下次查询2的集合号时才会更新。这正是并查集的妙处。

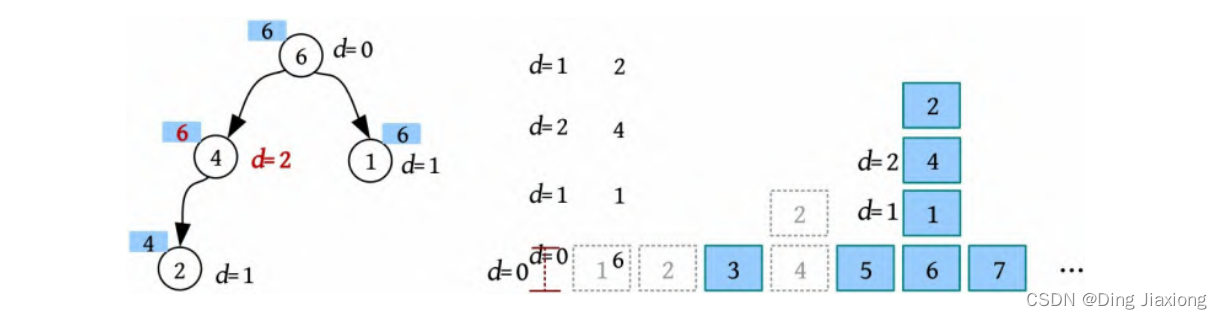
⑥ 查询。C 3：查询3下面有多少个方块。首先查询到3的集合号为3，d [3]=0。

⑦ 查询。C 4：查询4下面有多少个方块。首先查询4的集合号，在查询过程中将当前节点的集合号修改为其父节点的集合号，将当前节点的d 值加上其父节点的d 值，d [4]+=d [6]=2。

⑧ 若继续查询C 2，则查询2下面有多少个方块。先查询2的祖宗，在返回过程中将当前节点的d 值加上其父节点的d 值，d [2]+=d[4]=3。

【算法实现】

① 初始化。

void Init(){
	for(int i = 1;  i < N ; i ++){
		fa[i] = i; //每个方块的集合号 都为其自身
		d[i] = 0; //第i 个节点下方的方块数量 为0
		cnt[i] = 1; //第 i个栈 的方块数量为 1
	}
}

② 查询。查询x 的集合号，集合号等于自身时停止。在返回过程中，将经过路径上节点的集合号都统一为祖宗的集合号，将当前节点的d 值加上其父节点的d 值。

int Find(int x){
	int fx = fa[x];
	if(x != fa[x]){
		fa[x] = Find(fa[x]);
		d[x] += d[fx];
	}
	return fa[x];
}

③ 合并。首先找到x、y 所在的集合祖宗a 、b ，然后将a 的集合号修改为b ，更新d [a ]=cnt[b ]，cnt[b ]+=cnt[a ]。

void Union(int x, int y){
	int a , b;
	a = Find(x);
	b = Find(y);
	
	fa[a] = b;
	d[a] = cnt[b];
	cnt[b] += cnt[a];
}

[解决]

#include<cstdio>
#include<cstring>

using namespace std;

#define N 30010

int n , fa[N] , d[N] , cnt[N];

void Init(){
	for(int i = 1;  i < N ; i ++){
		fa[i] = i; //每个方块的集合号 都为其自身
		d[i] = 0; //第i 个节点下方的方块数量 为0
		cnt[i] = 1; //第 i个栈 的方块数量为 1
	}
}

int Find(int x){
	int fx = fa[x];
	if(x != fa[x]){
		fa[x] = Find(fa[x]);
		d[x] += d[fx];
	}
	return fa[x];
}

void Union(int x, int y){
	int a , b;
	a = Find(x);
	b = Find(y);
	
	fa[a] = b;
	d[a] = cnt[b];
	cnt[b] += cnt[a];
}

int main(){
	
	char op[3];
	
	int i , j;
	while(~scanf("%d" , &n)){
		
		Init();
		while(n --){
			
			scanf("%s", op);
			if(op[0] == 'C'){
				
				scanf("%d" , &i);
				int fi = Find(i);
				printf("%d\n" , d[i]);
			}
			else{
				
				scanf("%d%d" ,&i , &j);
				Union(i , j);
			}
		}
	}
	
	return 0;
}