矩阵空间

知识概要

​ 从矩阵空 间谈起，介绍矩阵空间的维数，基等问题。渗透一些微分方程与线性代数之间的 联系，并介绍秩为 1 的矩阵特点。

矩阵空间

对角阵D不是很理解。

（1）基与维数

再看对角阵 D，明显只有三个基:

即对角阵维数为 3，基正好为 S与U的交集。也可以写为: dim (SnU) = 3聊完交集，再考虑一下并集，之前向量空间中也介绍过，这样的两个子空间的并集不是向量空间，因为两个向量加和会脱离范围。
这个空间叫做:S+U，它与并集的不同就在于，并集只包含了 S 与U，而 S+U集合包含了它们两个的线性组合,就是任意对称阵加上任意上三角矩阵的和都包含于这个集合里。另外，很容易看出来，这个集合就是 M，所以 S+U 的维数是 9。联系上面的所有维数，有这样一个等式:
dim(S) + dim(u) = dim(Snu) + dim(S+U)

秩–矩阵

（1）秩–矩阵的优点

秩一矩阵的另外一个优点是它可以“搭建”其他矩阵，比如秩为 4 的矩阵， 通过四个秩一矩阵就能搭建出来。具体过程类似于矩阵乘法中的“列乘行”形式， 通过一列一行搭出一个矩阵。

（2）空间角度解释同秩矩阵

​ 那么从空间角度看，所有秩为 4 的矩阵构成的集合 M，能称之为空间么?肯定不是。其中都不包含零向量。另外，因为有这样一个性质存在:
​ R(A+B) ≤ R(A) + R(B)
​ 这就意味着 M 这个集合对加法也不封闭。两个秩为 4 的矩阵相加，结果的秩可能大于 4。所以所有秩为 4 的矩阵集合并不能构成空间。同理，秩为 1的矩阵集合也不能构成空间。

图

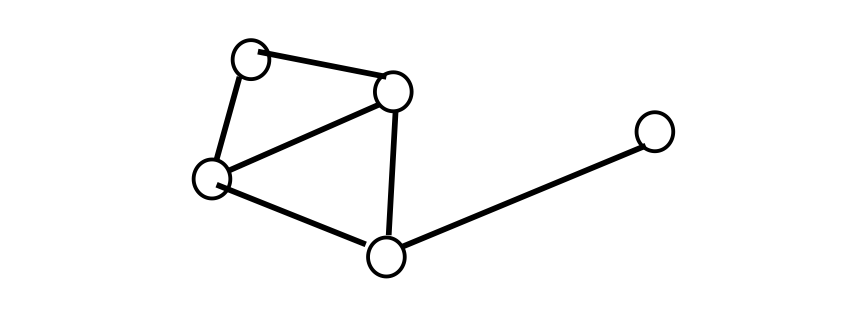
这个图包括五个节点和六条边，可以用一个 5*6 的矩阵来表示其中的所有信 息。详情请听下一章。