Bandit算法学习[网站优化]01——Multiarmed Bandit 算法引入

参考资料

White J. Bandit algorithms for website optimization[M]. " O’Reilly Media, Inc.", 2013.
https://github.com/johnmyleswhite/BanditsBook
easy-rl

一、探索与利用（exploration-exploitation）

在强化学习里面，探索和利用是两个很核心的问题。探索即我们去探索环境，通过尝试不同的动作来得到最佳的策略（带来最大奖励的策略）。利用即我们不去尝试新的动作，而是采取已知的可以带来很大奖励的动作。在刚开始的时候，强化学习智能体不知道它采取了某个动作后会发生什么，所以它只能通过试错去探索，所以探索就是通过试错来理解采取的动作到底可不可以带来好的奖励。利用是指我们直接采取已知的可以带来很好奖励的动作。所以这里就面临一个权衡问题，即怎么通过牺牲一些短期的奖励来理解动作，从而学习到更好的策略。

下面举一些探索和利用的例子。以选择餐馆为例，利用是指我们直接去我们最喜欢的餐馆，因为我们去过这个餐馆很多次了，所以我们知道这里面的菜都非常可口。探索是指我们用手机搜索一个新的餐馆，然后去尝试它的菜到底好不好吃。我们有可能对这个新的餐馆感到非常不满意，这样钱就浪费了。以做广告为例，利用是指我们直接采取最优的广告策略。探索是指我们换一种广告策略，看看这个新的广告策略可不可以得到更好的效果。以挖油为例，利用是指我们直接在已知的地方挖油，这样可以确保挖到油。探索是指我们在一个新的地方挖油，这样就有很大的概率可能不能发现油田，但也可能有比较小的概率可以发现一个非常大的油田。以玩游戏为例，利用是指我们总是采取某一种策略。比如，我们玩《街头霸王》游戏的时候，采取的策略可能是蹲在角落，然后一直出脚。这个策略很可能可以奏效，但可能遇到特定的对手就会失效。探索是指我们可能尝试一些新的招式，有可能我们会放出“大招”来，这样就可能“一招毙命”

与监督学习任务不同，强化学习任务的最终奖励在多步动作之后才能观察到，这里我们不妨先考虑比较简单的情形：最大化单步奖励，即仅考虑一步动作。需注意的是，即便在这样的简单情形下，强化学习仍与监督学习有显著不同，因为智能体需通过试错来发现各个动作产生的结果，而没有训练数据告诉智能体应当采取哪个动作。

想要最大化单步奖励需考虑两个方面：一是需知道每个动作带来的奖励，二是要执行奖励最大的动作。若每个动作对应的奖励是一个确定值，那么尝试遍所有的动作便能找出奖励最大的动作。然而，更一般的情形是，一个动作的奖励值是来自一个概率分布，仅通过一次尝试并不能确切地获得平均奖励值。

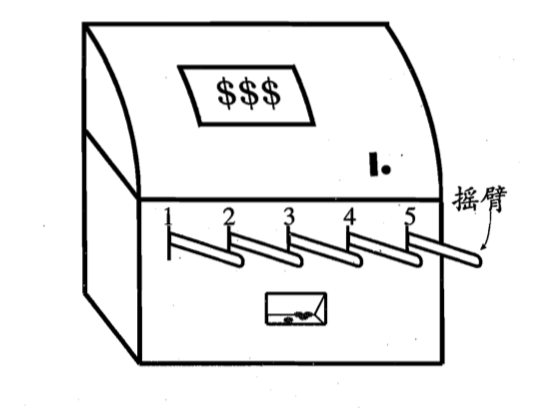
实际上，单步强化学习任务对应于一个理论模型，即K-臂赌博机（K-armed bandit），也被称为多臂赌博机**（multi-armed bandit）**。

如图 1.23 所示，K-臂赌博机有 K个摇臂，赌徒在投入一个硬币后可选择按下其中一个摇臂，每个摇臂以一定的概率吐出硬币，但这个概率赌徒并不知道。赌徒的目标是通过一定的策略最大化自己的奖励，即获得最多的硬币。若仅为获知每个摇臂的期望奖励，则可采用仅探索（exploration-only）法：将所有的尝试机会平均分配给每个摇臂（即轮流按下每个摇臂），最后以每个摇臂各自的平均吐币概率作为其奖励期望的近似估计。若仅为执行奖励最大的动作，则可采用仅利用（exploitation-only）法：按下目前最优的（即到目前为止平均奖励最大的）摇臂，若有多个摇臂同为最优，则从中随机选取一个。

显然，仅探索法能很好地估计每个摇臂的奖励，却会失去很多选择最优摇臂的机会；仅利用法则相反，它没有很好地估计摇臂期望奖励，很可能经常选不到最优摇臂。因此，这两种方法都难以使最终的累积奖励最大化。

事实上，探索（估计摇臂的优劣）和利用（选择当前最优摇臂)这两者是矛盾的，因为尝试次数（总投币数）有限，加强了一方则自然会削弱另一方，这就是强化学习所面临的探索-利用窘境（exploration-exploitation dilemma）。显然，想要累积奖励最大，则必须在探索与利用之间达成较好的折中。