文章目录
- 一、内容介绍
- 二、算法总结
- 2.1 二叉树结构
- 2.2 完整代码
- 2.3 输出结果
- 三、Reference
- 四、总结
一、内容介绍
上一年备考数据结构中自己整理并验证过的二叉树递归算法。包括:
1、二叉树的创建;
2、二叉树的先、中、后序的递归遍历;
3、输出二叉树中所有度为2的节点;
4、输出二叉树中所有度为1的节点;
5、输出二叉树中所有度为0的节点;
6、输出二叉树中所有节点的个数;
7、输出二叉树中所有节点的度数;
8、输出二叉树的高度;
9、输出二叉树先序遍历中第三个节点值;
10、输出二叉树先序遍历中data域为65的节点;
11、输出二叉树中 右孩子指针将二叉树的叶子节点从左向右链接成的单链表;
12、输出二叉树根节点的右孩子节点的层数;
二、算法总结
2.1 二叉树结构
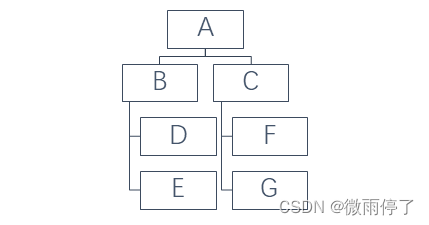
2.2 完整代码
#include<stdio.h>
#include<stdlib.h>
#include <iostream>
using namespace std;
//二叉树的链式存储结构
struct Tree{
char data;
// int data; //会自动转为ASCII码
struct Tree *lchild,*rchild;
};
//前序创建二叉树
void CreateTree(Tree **t) {
char ch;
cin >> ch;
//递归的终止条件,如果输入#号创建空指针,说明当前节点左子树已创建完毕
if (ch == '#')
*t = NULL;
else {
*t = new Tree;
(*t)->data = ch;
CreateTree(&((*t)->lchild));
CreateTree(&((*t)->rchild));
}
}
//二叉树的三种遍历
void visit(Tree *t){
//对结点的一些操作
cout << t->data << " ";
}
//先序
void preorder(Tree *t){
if(t!=NULL){
visit(t);
preorder(t->lchild);
preorder(t->rchild);
}
}
//中序
void inorder(Tree *t){
if(t!=NULL){
inorder(t->lchild);
visit(t);
inorder(t->rchild);
}
}
//后序
void postorder(Tree *t){
if(t!=NULL){
postorder(t->lchild);
postorder(t->rchild);
visit(t);
}
}
//计算二叉树的所有双分支节点(度为2)节点个数
int Degree_2(Tree *t){
if(t==NULL){ //为空节点
return 0;
}else if(t->lchild!=NULL && t->rchild!=NULL){ //为双分支节点
return Degree_2(t->lchild)+Degree_2(t->rchild)+1; //双分支节点个数=递归的双分支节点数+自己
}else{ //为单分支节点
return Degree_2(t->lchild)+Degree_2(t->rchild); //双分支节点个数=递归的双分支节点数
}
}
//计算二叉树的所有单分支节点(度为1)节点个数
int Degree_1(Tree *t){
if(t==NULL){
return 0;
}else if(t->lchild!=NULL && t->rchild==NULL || t->lchild==NULL && t->rchild!=NULL){ //单分支节点
return Degree_1(t->lchild)+Degree_1(t->rchild)+1;
}else{
return Degree_1(t->lchild)+Degree_1(t->rchild);
}
}
//计算二叉树的所有叶子节点(度为0)节点个数
int Degree_0(Tree *t){
if(t==NULL){
return 0;
}else if(t->lchild==NULL && t->rchild==NULL){
return 1;
}else{
return Degree_0(t->lchild)+Degree_0(t->rchild);
}
}
//计算二叉树的所有节点个数
int n = 0;
int count(Tree *t){
if(t!=NULL){
++n; //先序:根节点visit()改写,每次递归,n=n+1
count(t->lchild);
count(t->rchild);
}
return n;
}
//计算二叉树高度
int depth(Tree *t){
if(t==NULL){
return 0; //递归到空树,返回0
}else{
int lh = depth(t->lchild); //递归求左子树高
int rh = depth(t->rchild); //递归求右子树高
if(lh>=rh){
return lh+1;
}else{
return rh+1;
}
}
}
//把二叉树中所有节点的左右子树交换
void swap(Tree *t) {
if(t!=NULL){
Tree *temp = new Tree(); //临时变量
temp = t->lchild;
t->lchild = t->rchild;
t->rchild = temp;
swap(t->lchild); //递归交换左
swap(t->rchild); //递归交换右
}
}
//求二叉树先序遍历中的第k个节点值
int i = 0;
void find_k(Tree *t, int k){
if(t!=NULL){
++i; //visit()
if(k==i){
cout<< t->data;
return;
}else{
find_k(t->lchild,k); //递归查左
find_k(t->rchild,k); //递归查右边
}
}
}
//查找二叉树data域等于key的节点是否存在,若存在,将q指向它,否则q为空
void find_key(Tree *t,Tree *q,int key){
if(t!=NULL){
if(t->data==key){ //找到
q=t;
cout<<q->data;
}else{
find_key(t->lchild,t,key); //递归查左
find_key(t->rchild,t,key); //递归查右
}
}
}
//利用节点的右孩子指针将一个二叉树的叶子节点从左向右链接成一个单链表(head指向第一个,tail指向最后一个)
void link(Tree *t,Tree *head,Tree *tail){
if(t!=NULL){
if(t->lchild==NULL&&t->rchild==NULL){ //叶子节点
if(head==NULL){ //还未指向时
head=t;
tail=t;
}
tail->rchild=t; //链接
tail=t;
cout<<t->data<< " ";
}else{ //非叶子节点,递归
link(t->lchild,head,tail);
link(t->rchild,head,tail);
}
}
}
int h=0;
//求出指定节点在二叉排序树中的层次
//中序遍历二叉排序树得一个递增的序列
int find_ceng(Tree *t,Tree *p) {
if(t!=NULL){
Tree *head=t;
if(head!=NULL){
while(head->data!=p->data){
if(head->data<=p->data){
head=head->rchild;
}else{
head=head->lchild;
}
++h;
}
return h;
}
}
}
//求二叉树的带权路径长度
int wpl_inorder(Tree *t,int deep){
int wpl=0;
if(t!=NULL){
if(t->lchild==NULL&&t->rchild==NULL){ //叶子节点
// cout<<int(t->data);
wpl+=(int(t->data))*deep;
}
// cout<<"here2";
if(t->lchild!=NULL)
wpl_inorder(t->lchild,deep+1); //递归左
if(t->rchild!=NULL)
wpl_inorder(t->rchild,deep+1); //递归右
return wpl;
}
}
int main(){
Tree *t;
cout << "请按先序遍历的顺序创建二叉树,ABD##E##CF##G##" << endl;
CreateTree(&t);
cout << "先序遍历的结果为:";
preorder(t) ;
cout << endl;
cout << "中序遍历的结果为:";
inorder(t) ;
cout << endl;
cout << "后序遍历的结果为:";
postorder(t) ;
cout << endl;
cout << "二叉树中所有度为2的节点:";
cout << Degree_2(t);
cout << endl;
cout << "二叉树中所有度为1的节点:";
cout << Degree_1(t);
cout << endl;
cout << "二叉树中所有度为0的节点:";
cout << Degree_0(t);
cout << endl;
cout << "二叉树的所有节点个数:";
cout << count(t);
cout << endl;
cout << "二叉树的高度:";
cout << depth(t);
cout << endl;
cout << "二叉树先序遍历中的第3个节点值 :";
find_k(t,3);
cout << endl;
cout << "二叉树先序遍历中data域等于65的节点 :";
Tree *q = NULL;
find_key(t,q,65);
cout << endl;
cout << "右孩子指针将二叉树的叶子节点从左向右链接成一个单链表:";
Tree *head = NULL;
Tree *tail = NULL;
link(t,head,tail);
cout << endl;
cout << "求二叉树根节点的右孩子节点的层次:";
Tree *p = t->rchild;
cout << find_ceng(t,p);
cout << endl;
// cout << "求二叉树的wpl:";
// cout << wpl_inorder(t,0);
// cout << endl;
}
2.3 输出结果
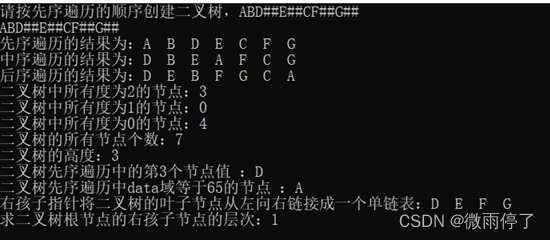
三、Reference
大师兄的手把手教你写考研数据结构代码题:https://www.bilibili.com/video/BV1hQ4y1R7Tw
四、总结
这份总结分享给有需要的同学们。也希望2022年自己的努力,开花结果。
2023年1月3日于家中。
![[项目说明]-基于人工智能博弈树,极大极小(Minimax)搜索算法并使用Alpha-Beta剪枝算法优化实现的可人机博弈的AI智能五子棋游戏。](https://img-blog.csdnimg.cn/a37a67a97ec2444688af952eefe7c005.png)