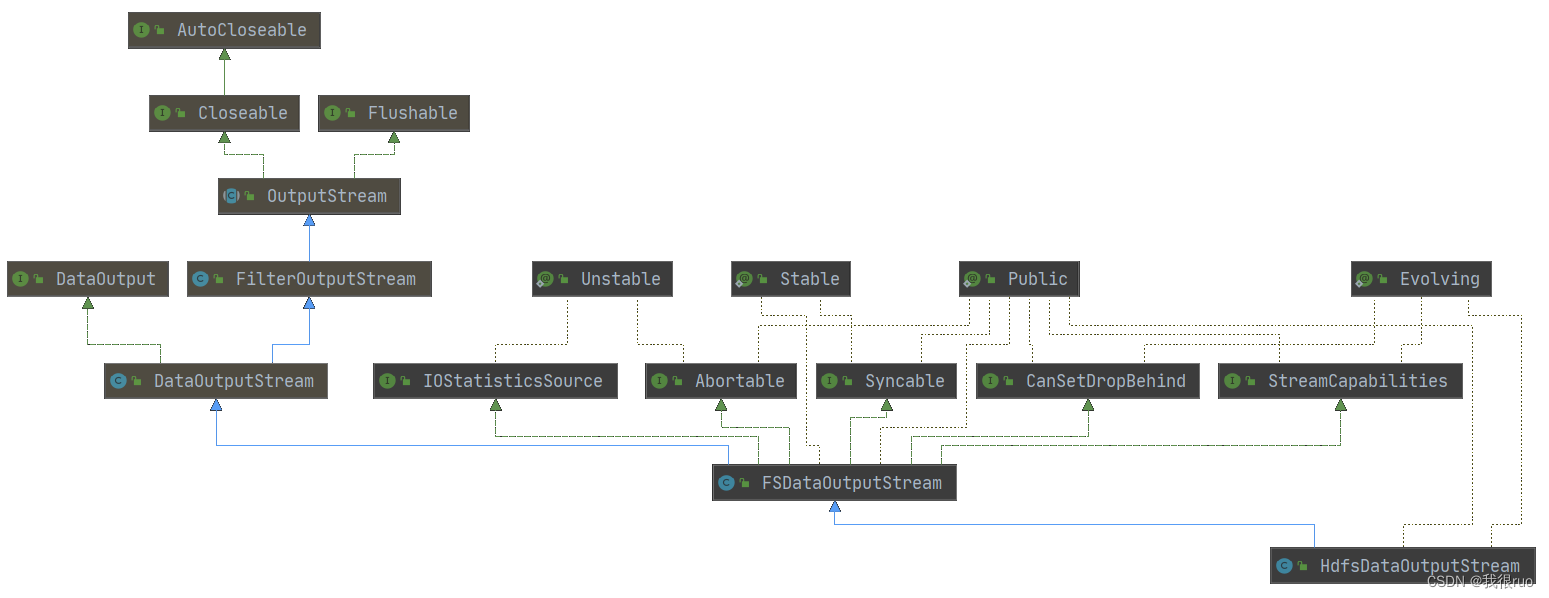
循环队列

front：头指针

rear：尾指针

m：循环队列的长度

元素个数=（rear-front+m）%m

19-11+40=48%40=8

11-19+40=32%40=32

二叉树

入度=出度，n-1=n0+n1+n2-1=n1+2n2,有n2+1=n0,对于完全二叉树，度为1的节点要么只有1个，要么没有，n=n0+n1+n2=2n2+n1+1,由于为偶数，所以N1为奇数，即n1=1,所以n2=15,n0=16 

在先序里确定根节点，然后划分左右子树，A

查找

12个元素，左指针为1，右指针12，1+12>>1=6.5=6,65

左指针为6，右指针12，6+12>>1=9,80

左指针6，右指针9，6+9>>1=7.5=7,70

左指针7，右指针9，8；；经过了4次比较

堆

朴素建堆是加到最后，然后一直往上进行操作，如果比上面大，就和上面交换，直到不能交换为止，即上面比现在的大；

快速建堆是，先输入所有的序列，然后从第一个非叶子节点开始，向下进行操作，维护从下至上一直是大根堆，这样在上面的时候，向下比较，通往下面的路径就都是有序的，递减的，所以交换的时候，就是向下调整，直到不比下面的小，就是最后的位置

如果是要建小根堆，就向下找两个孩子最小的；要建大根堆，就找两个孩子最大的，为了防止选出另一个孩子后，依然不满足要求，就需要再次调整，就很麻烦，所以就直接选最小或最大的，就不用再进行调整了

向下调整，就是找这个节点中最大/最小的孩子，换上来

或者向下调整可以看成是在向下的路径牌堆中找到合适的位置，就是插入排序，插入操作 C

顺序表

如果是要删除的话，删除第一个元素，移动的次数为N-1,删除最后一个元素移动的次数为0，其它平均分布在这之间，所以是（N-1)/2

往顺序表中插入元素时，有N个时，最多移动N次，即放在顺序表的头部，N个元素都要动；最少0次，即插在队尾，其它情况就平均分布在这中间，所以平均就是二分之N

在顺序表中，逻辑上相邻的两个元素物理存储上也一定相邻（对）

某顺序表的第一个元素的存储地址是500，每个元素占4个单元，则第8个元素的起始地址是（D）

A.504 B.508 C.516 D.528

长度为n的非空线性表采用顺序存储结构，在第i个元素前插入一个数据元素，i的合法值应该是（A)

A.1<=i<=n+1 B.0<=i<=n+1 C.i>0 D.1<=i<=n-1

（取n+1就是在队尾插入元素）

在长度为n的顺序表中的第i（1<=i<=n+1）个元素前插入一个元素，需要移动的元素个数为（B)

A.n-i B.n-i+1 C.i D.n-i-1（就是i~n区间里元素的个数，为n-i+1)

在长度为n的顺序表中的第i（1<=i<=n+1）个元素前删除一个元素，需要移动的元素个数为（A)

A…n-i B.n-i+1 C.n-i-1 D.i

假设删除长度为n的顺序表中的每个元素的概率相同，则删除一个元素平均要移动的元素的个数是（D)
A.n/2 B.(n+1)/2 C.n D.(n-1)/2

在长度为n的顺序表中的第i（1<=i<=n+1）个元素前插入一个元素，其算法复杂度为（B）

A.O(1) B.O(n）C.O(n*n) D.O(logn)(以2为底）

在长度为n的顺序表中读取第i（1<=i<=n+1）个元素，其算法复杂度为（A）这道题考察的是getelem,不是定位操作locateelem

A.O(1) B.O(n）C.O(n*n) D.O(logn)(以2为底）

在长度为n的顺序表中删除第i（1<=i<=n+1）个元素，其算法复杂度为（B）
A.O(1) B.O(n）C.O(n*n) D.O(logn)(以2为底)

生成树

所有边权均不相同的无向图最小生成树是唯一的

同一个图不同最小生成树的边权重序列相同。

都可有K算法得出 

哈夫曼树

 

这个路径指的是节点到节点那个棍子的数量，而不是节点和节点间的节点数量 

初始时会入队13个叶子节点，然后每次操作都会减少队列中一个节点，生成一个非叶子节点，直到留下一个根节点，总共操作12次，产生12个非叶子节点，所以一共有25个节点

排序

停止时，左指针指向6，右指针指向3，然后交换，交换后左右指针移动，左指针指向6，右指针指向3，且左指针比右指针大，那么3和5交换，即3，2，5，6，8