一、最优二叉树
1、定义
官方定义:在权值为w1,w2,…,wn的 n个叶子所构成的所有二叉树中,带权路径长度最小(即代价最小)的二叉树称为
最优二叉树或哈夫曼树。
通俗来讲,就是给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树(Full Binary Tree)或者哈夫曼树(Huffman Tree)。
哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
2、几个概念
2.1 路径长度
路径是从树中一个结点到另一个结点之间的通路,路径上的分支数(边)称为它的路径长度。
2.2 树的路径长度
树的路径长度是从树根到每一叶子结点之间的路径长度之和。
2.3 树的带权路径长度(WPL)
树的带权路径长度(Weighted Path Length of Tree,简记为WPL):定义为树中所有叶子结点的带权路径长度之和.
- 结点的权值:在一些应用中,赋予树中结点的一个有某种意义的实数。
- 结点的带权路径长度:从该结点到树根之间的路径长度与该结点上权值的乘积。
2.4 示例:计算WPL
计算下面三颗二叉树的带权路径长度总和,其中每个点的权重为:a(7), b(5), c(2), d(4)。
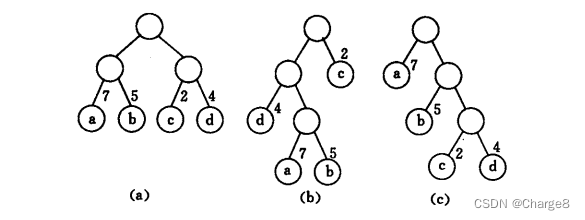
WPL(a):7*2 + 5*2 + 2*2 + 4*2 = 36
WPL(b):7*3 + 5*3 + 2*1 + 4*2 = 46
WPL(c):7*1 + 5*2 + 2*3 + 4*3 = 35
其中 ©树的 WPL最小,可以验证,它就是哈夫曼树。
注意:
- 叶子上的权值均相同时,完全二叉树一定是最优二叉树,否则完全二叉树不一定是最优二叉树。
- 最优二叉树中,权越大的叶子离根越近。
- 最优二叉树的形态不唯一,WPL最小。
3、哈夫曼编码
任一字符的编码都不是另一个字符的编码的前缀,这种编码称为
哈夫曼编码,也称为前缀码。
我们可以:
- 根据所提供的字母数据建立一个 Huffman树;
- 根据生成的 Huffman树的结构,显示输出所有字母的Huffman编码。
比如:在上图的最优二叉树中我们给每一条边加上一个权值,指向左子节点的边我们标记为0,指向右子节点的边标记为1,那从根节点到叶节点的路径就是我们说的哈夫曼编码。
所以图c的赫夫曼树对应的编码就是:
a:0
b:10
c:110
d:111
4、哈夫曼算法
对于给定的叶子数目及其权值构造最优二叉树的方法,由于这个算法是哈夫曼提出来的,故称其为哈夫曼算法。
其基本思想是:
(1)根据给定的n个权值w1,w2,…,wn构成n棵二叉树的森林F={T1,T2,…,Tn},其中每棵二叉树Ti中都只有一个权值为wi的根结点,其左右子树均空。
(2)在森林F中选出两棵根结点权值最小的树(当这样的树不止两棵树时,可以从中任选两棵),将这两棵树合并成一棵新树,为了保证新树仍是二叉树,需要增加一个新结点作为新树的根,并将所选的两棵树的根分别作为新根的左右孩子(谁左,谁右无关紧要),将这两个孩子的权值之和作为新树根的权值。
(3)对新的森林F重复(2),直到森林F中只剩下一棵树为止。这棵树便是哈夫曼树。
注意:
- 初始森林中的n棵二叉树,每棵树有一个孤立的结点,它们既是根,又是叶子
- n个叶子的哈夫曼树要经过n-1次合并,产生n-1个新结点。最终求得的哈夫曼树中共有2n-1个结点。
- 哈夫曼树是严格的二叉树,没有度数为1的分支结点。
4.1 核心思想和实现思路
核心思想:
使用贪心算法:利用局部最优推出全局最优,把频率出现多的用短码表示,频率出现小的就用长一点。而且,任何一个字符的编码都不是另一个的前缀,在解压缩的时候,我们每次会读取尽可能长的可解压的二进制串,所以在解压缩的时候也不会产生歧义。
具体实现思路:
- 每次取数值最小的两个节点,将之组成为一颗子树。
- 移除原来的两个点
- 然后将组成的子树放入原来的序列中
- 重复执行1 2 3 直到只剩最后一个点
二、代码实现
1、示例
例子: a:3 b:24 c:6 d:20 e:34 f:4 g:12
根据以上权重来实现哈夫曼树。
1)数据结点
public class HuffmanNode implements Comparable<HuffmanNode> { // 优先队列,小的我把你优先级调高
String chars; // 节点里面的字符
int fre; // 表示是频率
HuffmanNode left;
HuffmanNode right;
HuffmanNode parent; // 用来找上层的
@Override
public int compareTo(HuffmanNode o) {
return this.fre - o.fre;
}
}
2)哈夫曼树
public class HuffmanTree {
HuffmanNode root;
List<HuffmanNode> leafs; // 叶子节点
Map<Character, Integer> weights; // 叶子节点的权重, a,b,c,d,e
public HuffmanTree(Map<Character, Integer> weights) {
this.weights = weights;
leafs = new ArrayList<HuffmanNode>();
}
/**
* 叶子节点进行编码
*
* @return
*/
public Map<Character, String> code() {
Map<Character, String> map = new HashMap<Character, String>();
for (HuffmanNode node : leafs) {
String code = "";
Character c = new Character(node.chars.charAt(0)); // 叶子节点肯定只有一个字符
HuffmanNode current = node; // 只有一个点
do {
if (current.parent != null && current == current.parent.left) { // 说明当前点是左边
code = "0" + code;
} else {
code = "1" + code;
}
current = current.parent;
} while (current.parent != null); // parent == null就表示到了根节点
map.put(c, code);
}
return map;
}
/**
* 生成哈夫曼树
*/
public void creatTree() {
Character keys[] = weights.keySet().toArray(new Character[0]); // 拿出所有的点
/**
* jdk底层的优先队列
*/
PriorityQueue<HuffmanNode> priorityQueue = new PriorityQueue<HuffmanNode>();
for (Character c : keys) {
HuffmanNode hfmNode = new HuffmanNode();
hfmNode.chars = c.toString();
hfmNode.fre = weights.get(c); // 权重
priorityQueue.add(hfmNode); // 首先把我们的优先队列初始化进去
leafs.add(hfmNode);
}
int len = priorityQueue.size();
for (int i = 1; i <= len - 1; i++) { // 每次找最小的两个点合并
HuffmanNode n1 = priorityQueue.poll(); //
HuffmanNode n2 = priorityQueue.poll(); // 每次取优先队列的前面两个 就一定是两个最小的
HuffmanNode newNode = new HuffmanNode();
newNode.chars = n1.chars + n2.chars; // 我们把值赋值一下,也可以不复制
newNode.fre = n1.fre + n2.fre; // 把权重相加
// 维护出树的结构
newNode.left = n1;
newNode.right = n2;
n1.parent = newNode;
n2.parent = newNode;
priorityQueue.add(newNode);
}
root = priorityQueue.poll(); // 最后这个点就是我们的根节点
System.out.println("构建完成");
}
}
3)测试
public static void main(String[] args) {
/**
* 示例:a:3 b:24 c:6 d:20 e:34 f:4 g:12
*/
Map<Character, Integer> weights = new HashMap<Character, Integer>();
// 初始化密码本
weights.put('a', 3);
weights.put('b', 24);
weights.put('c', 6);
weights.put('d', 1);
weights.put('e', 34);
weights.put('f', 4);
weights.put('g', 12);
HuffmanTree huffmanTree = new HuffmanTree(weights);
huffmanTree.creatTree();
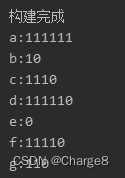
Map<Character, String> code = huffmanTree.code();
code.forEach((k, v) -> {
System.out.println(k + ":" + v);
});
}
– 求知若饥,虚心若愚。