线性回归

有监督学习中主要解决两个问题，一个是分类，另一个是回归。
在回归问题中，我们需要利用我们已知的特征 $x_1,x_2,...,x_p$ 去预测我们的目标变量 $y$ 。注意这里 $y$ 是连续变量。一个简单的例子就是用一个人的身高去估计或者说预测体重。

线性回归的公式如下：
$\hat{y}(w, x)=w_{0}+w_{1} x_{1}+\ldots+w_{p} x_{p}$

其中 $w_0$ 是截距参数， $w_1,...,w_p$ 是模型斜率参数。通过这样的线性组合我们就能给出一个预测 $\hat{y}$ 。

下面我们来看具体的一个代码例子。

# 导入必要的 python 库
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from sklearn.metrics import mean_squared_error, r2_score

# 数据准备
# 身高 （cm）
X = np.array([150,155,160,175,180,185,190,195])
# 体重 (kg)
y = np.array([50,55,60,75,81,84,93,92])


# 将数据切分成训练集和测试集
X_train = X[:-4].reshape((-1,1))
X_test = X[-4:].reshape((-1,1))

y_train = y[:-4]
y_test = y[-4:]

# 创建线性回归对象
regr = linear_model.LinearRegression()

# 使用训练集训练模型
regr.fit(X_train, y_train)

# 使用测试集特征数据做预测
y_pred = regr.predict(X_test)

# 模型系数
print("Coefficients: \n", regr.coef_)
# 模型的均方误差
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
# 模型的决定系数 R 方，越接近 1 模型解释力越强
print("Coefficient of determination: %.2f" % r2_score(y_test, y_pred))

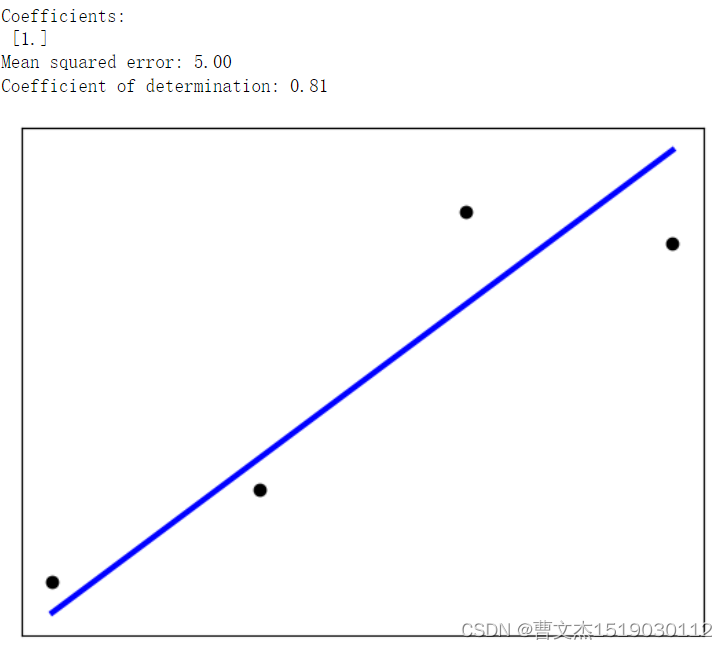
# 绘制散点图
plt.scatter(X_test, y_test, color="black")
plt.plot(X_test, y_pred, color="blue", linewidth=3)

plt.xticks(())
plt.yticks(())

plt.show()