矩阵中的最长递增路径

news2024/11/16 11:32:38

题目链接

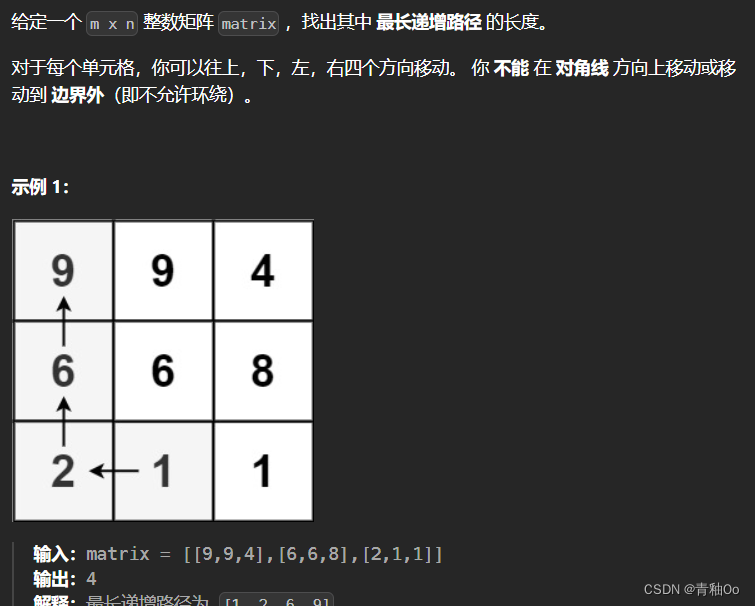
矩阵中的最长递增路径

题目描述

注意点

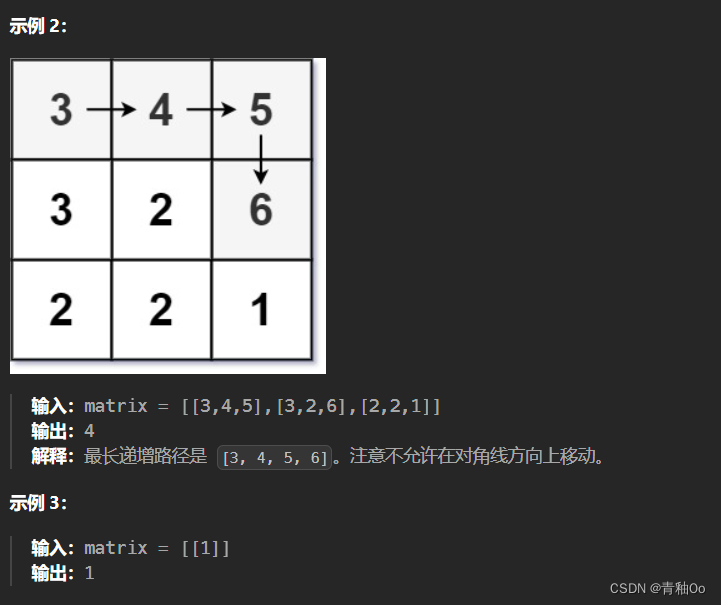
不能在对角线方向上移动或移动到边界外（即不允许环绕）

解答思路

因为最长递增路径一定是连续的，所以想到使用深度优先遍历来做。如果只使用深度优先遍历会导致超时（同一个节点的最长递增路径可能会计算多次），所以考虑引入动态规划存储每个节点的最长递增路径。除此之外，还要进行剪枝，主要是解决边界问题和移动后的值小于当前值的情况

代码

class Solution {
    int row;
    int col;
    int[][] directions;
    public int longestIncreasingPath(int[][] matrix) {
        int res = 0;
        row = matrix.length;
        col = matrix[0].length;
        directions = new int[][] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
        int[][] dp = new int[row][col];
        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                res = Math.max(res, findMaxPath(matrix, dp, i, j));
            }
        }
        return res;
    }

    public int findMaxPath(int[][] matrix, int[][] dp, int i, int j) {
        if (dp[i][j] != 0) {
            return dp[i][j];
        }
        int maxPath = 0;
        for (int[] direction : directions) {
            int x = i + direction[0];
            int y = j + direction[1];
            if (x < 0 || x >= row || y < 0 || y >= col) {
                continue;
            }
            if (matrix[x][y] <= matrix[i][j]) {
                continue;
            }
            maxPath = Math.max(maxPath, findMaxPath(matrix, dp, x, y));
        }
        dp[i][j] = maxPath + 1;
        return dp[i][j];
    }
}