文章目录
- 一、题目
- 二、解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
一、题目

二、解法
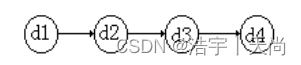
思路分析:因为每次可以爬1阶或者2阶台阶,若想到达第i阶,则有两种情况:在第i-2阶台阶处一次爬2阶(如果一次一阶爬两次到第i阶的情况属于后面一种),或者是在第i-1阶一次爬1阶。假设dp数组代表到达第i阶的方法,那么根据上述分析,有
d
p
[
i
]
=
d
p
[
i
−
1
]
+
d
p
[
i
−
2
]
dp[i]=dp[i-1]+dp[i-2]
dp[i]=dp[i−1]+dp[i−2]。
程序如下:
class Solution {
public:
int climbStairs(int n) { // 1 1 2 3 5 8 13 21
//if (n < 1) return 0; // n在[1,45]之间
vector<int> dp(n + 1); // 动态规划中的dp数组
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( n ) O(n) O(n)。
同样,我们只用到了两个数,进行算法优化,将空间复杂度降低到O(1)。程序如下:
class Solution {
public:
int climbStairs(int n) { // 1 1 2 3 5 8 13 21
//if (n < 1) return 0; // n在[1,45]之间
vector<int> dp(n + 1); // 动态规划中的dp数组
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
复杂度分析:
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
三、完整代码
# include <iostream>
# include <vector>
using namespace std;
//class Solution {
//public:
// int climbStairs(int n) { // 1 1 2 3 5 8 13 21
// //if (n < 1) return 0; // n在[1,45]之间
// vector<int> dp(n + 1); // 动态规划中的dp数组
// dp[0] = 1;
// dp[1] = 1;
// for (int i = 2; i <= n; i++) {
// dp[i] = dp[i - 1] + dp[i - 2];
// }
// return dp[n];
// }
//};
class Solution {
public:
int climbStairs(int n) {
int dp[2] = {1, 1};
for (int i = 2; i <= n; i++) {
int sum = dp[0] + dp[1];
dp[0] = dp[1];
dp[1] = sum;
}
return dp[1];
}
};
int main() {
int n = 4;
Solution s1;
int result = s1.climbStairs(n);
cout << result << endl;
system("pause");
return 0;
}
end