XI`AN TECHNOLOGICAL UNIVERSITY

课程设计报告

1绪论

2课程设计目的和内容

3算法的基本思想

1 .建立二叉树结构

建立二叉树时，要先明确是按哪一种遍历规则输入，该二叉树是按你所输入的遍历规则来建立的。本实验用的先序遍历行建树。二叉树用链表存储来实现，因此要先定义一个二叉树链表存储结构。因此要先定义一个结构体。此结构体的每个结点都是由数据域data、左指针域Lchild、右指针域Rchild组成，两个指针域分别指向该结点的左、右孩子。

2. 输入二叉树元素

输入二叉树时，是按上面所确定的遍历规则输入的。最后，用一个返回值来表示所需要的结果.

3. 先序遍历二叉树

当二叉树为非空时，执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

4. 中序遍历二叉树

当二叉树为非空时，程序执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

5. 后序遍历二叉树

当二叉树为非空时，程序执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

6. 非递归方式的先序遍历：

① 输出节点P，然后将其入栈，再看P的左孩子是否为空；

② 若P的左孩子不为空，则置P的左孩子为当前节点，重复①的操作；

③ 若P的左孩子为空，则将栈顶节点出栈，但不输出，并将出栈节点的右孩子置为当前节点，看其是否为空；

④ 若不为空，则循环至①操作；

⑤ 如果为空，则继续出栈，但不输出，同时将出栈节点的右孩子置为当前节点，看其是否为空，重复④和⑤操作；

⑥ 直到当前节点P为NULL并且栈空，遍历结束。

7. 非递归方式的中序遍历：

① 若P的左孩子不为空，则将P入栈并将P的左孩子置为当前节点，然后再对当前节点进行相同的处理；

② 若P的左孩子为空，则输出P节点，而后将P的右孩子置为当前节点，看其是否为空；

③ 若不为空，则重复①和②的操作；

④ 若为空，则执行出栈操作，输出栈顶节点，并将出栈的节点的右孩子置为当前节点，看起是否为空，重复③和④的操作；

⑤ 直到当前节点P为NULL并且栈为空，则遍历结束。

8. 非递归的后序遍历：

① 先将节点P入栈；

② 若P不存在左孩子和右孩子，或者P存在左孩子或右孩子，但左右孩子已经被输出，则可以直接输出节点P，并将其出栈，将出栈节点P标记为上一个输出的节点，再将此时的栈顶结点设为当前节点；

③ 若不满足②中的条件，则将P的右孩子和左孩子依次入栈，当前节点重新置为栈顶结点，之后重复操作②；

④ 直到栈空，遍历结束。

9. 层次遍历二叉树：

4测试数据

5.源程序

5心得体会

源码

课程设计报告

实验课程名称

专业：

班级：

姓名：

学号：

实验学时：

指导教师：

成绩：

年月

1绪论

现代社会生活中，计算机扮演着重要角色，而随着计算机运行速度的不断加快，对数据的处理能力也日益增强，因此，程序所涉及的数据很多，如何科学有效的对数据进行操作，使得计算机的时间和空间利用率最高是一个问题。针对这样的问题，我选择了二叉树对数据的各种操作作为我的课程设计主题，希望通过二叉树来提高对数据的处理能力，促进对数据结构课程的理解。

在二叉树的应用中，常常要求在树中查找具有某种特征的结点，或者对树中全部结点逐一进行某种处理，这就是二叉树的遍历问题。

对二叉树的数据结构进行定义，建立一颗二叉树，然后进行各种实验操作。

2课程设计目的和内容

（1）问题分析：建立一个二叉树，并对其进行4种遍历(前中后层)

（2）功能要求：使用递归和非递归，计算二叉树中节点的个数，树的深度等

（3）输入的形式和输入值的范围：采用c语言、自我实现栈和队列的代码

输入值为一个可以满足二叉树存在的先序遍历序列

（4）输出的形式：（通过自己进行终端输入），递归输出二叉树的先序遍历、中序遍历、后序遍历，非递归二叉树的先序遍历、中序遍历、后序遍历（使用栈），二叉树的层序遍历（使用队列），计算二叉树中结点个数的计算，实现树的深度的计算

3算法的基本思想

1 .建立二叉树结构

建立二叉树时，要先明确是按哪一种遍历规则输入，该二叉树是按你所输入的遍历规则来建立的。本实验用的先序遍历行建树。二叉树用链表存储来实现，因此要先定义一个二叉树链表存储结构。因此要先定义一个结构体。此结构体的每个结点都是由数据域data、左指针域Lchild、右指针域Rchild组成，两个指针域分别指向该结点的左、右孩子。

2. 输入二叉树元素

输入二叉树时，是按上面所确定的遍历规则输入的。最后，用一个返回值来表示所需要的结果.

3. 先序遍历二叉树

当二叉树为非空时，执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

4. 中序遍历二叉树

当二叉树为非空时，程序执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

5. 后序遍历二叉树

当二叉树为非空时，程序执行以下三个操作：访问根结点、先序遍历左子树、先序遍历右子树。

6. 非递归方式的先序遍历：

① 输出节点P，然后将其入栈，再看P的左孩子是否为空；

② 若P的左孩子不为空，则置P的左孩子为当前节点，重复①的操作；

③ 若P的左孩子为空，则将栈顶节点出栈，但不输出，并将出栈节点的右孩子置为当前节点，看其是否为空；

④ 若不为空，则循环至①操作；

⑤ 如果为空，则继续出栈，但不输出，同时将出栈节点的右孩子置为当前节点，看其是否为空，重复④和⑤操作；

⑥ 直到当前节点P为NULL并且栈空，遍历结束。

7. 非递归方式的中序遍历：

① 若P的左孩子不为空，则将P入栈并将P的左孩子置为当前节点，然后再对当前节点进行相同的处理；

② 若P的左孩子为空，则输出P节点，而后将P的右孩子置为当前节点，看其是否为空；

③ 若不为空，则重复①和②的操作；

④ 若为空，则执行出栈操作，输出栈顶节点，并将出栈的节点的右孩子置为当前节点，看起是否为空，重复③和④的操作；

⑤ 直到当前节点P为NULL并且栈为空，则遍历结束。

8. 非递归的后序遍历：

① 先将节点P入栈；

② 若P不存在左孩子和右孩子，或者P存在左孩子或右孩子，但左右孩子已经被输出，则可以直接输出节点P，并将其出栈，将出栈节点P标记为上一个输出的节点，再将此时的栈顶结点设为当前节点；

③ 若不满足②中的条件，则将P的右孩子和左孩子依次入栈，当前节点重新置为栈顶结点，之后重复操作②；

④ 直到栈空，遍历结束。

9. 层次遍历二叉树：

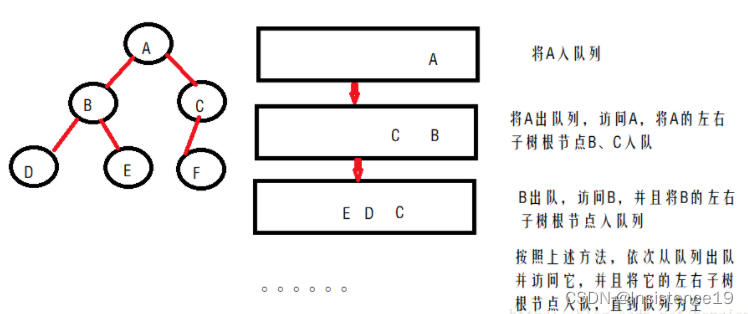
10. 计算根节点的个数

11. 计算二叉树的深度

4测试数据

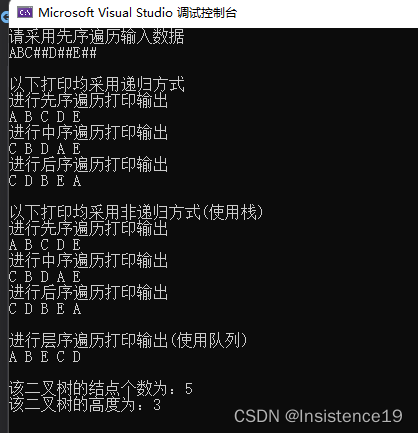
5.源程序

#include<stdio.h>

#include<stdlib.h>

#include<assert.h>

#include<string.h>

//建立一个二叉树，并对其进行4种遍历(前中后层)。

//[要求] 使用递归和非递归，计算二叉树中节点的个数，树的深度。

// 使用c语言

// 树结构体

typedef struct _BNode

{

char m_value;

struct _BNode* m_left;

struct _BNode* m_right;

}BNode;

// 存放树结点的栈结构体

typedef struct BNode* DataType;

typedef struct _Stack

{

DataType* array;

int capacity;

int size;

}Stack;

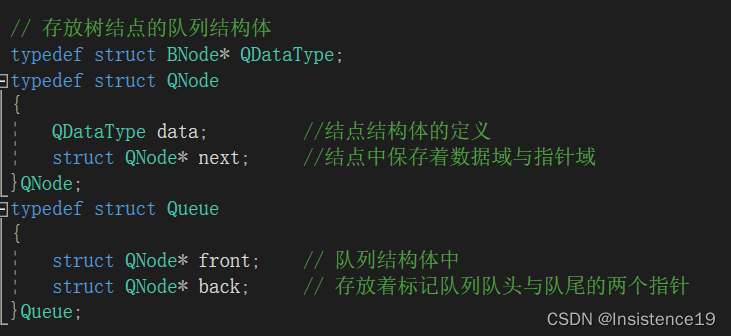
// 存放树结点的队列结构体

typedef struct BNode* QDataType;

typedef struct QNode

{

QDataType data; //结点结构体的定义

struct QNode* next; //结点中保存着数据域与指针域

}QNode;

typedef struct Queue

{

struct QNode* front; // 队列结构体中

struct QNode* back; // 存放着标记队列队头与队尾的两个指针

}Queue;

QNode* QueueBuyNode(QDataType data)

{

QNode* newnode = (QNode*)malloc(sizeof(QNode));

if (NULL == newnode)

{

assert(0);

printf("BuyNode !!!\n");

}

newnode->data = data;

newnode->next = NULL;

return newnode;

}

// 初始化队列

void QueueInit(Queue* q)

{

assert(q);

q->back = NULL;

q->front = NULL;

}

// 队尾入队列

void QueuePush(Queue* q, QDataType data)

{

assert(q);

// 0、创建一个新结点进行尾插

QNode* newnode = QueueBuyNode(data);

// 1、队列中没有结点

if (QueueEmpty(q))

{

q->front = newnode;

q->back = newnode;

}

else

{

// 2、队列中有结点

q->back->next = newnode;

q->back = newnode;

}

// 队头出队列

void QueuePop(Queue* q)

{

assert(q);

// 1、队列中没有元素

if (QueueEmpty(q))

return;

// 2、队列中只有一个元素

else if (q->back == q->front)

{

free(q->front);

q->front = NULL;

q->back = NULL;

}

// 3、队列中有多个元素

else

{

QNode* del = q->front;

q->front = del->next;

free(del);

}

// 获取队列头部元素

QDataType Queuefront(Queue* q)

{

assert(q);

return q->front->data;

}

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0

int QueueEmpty(Queue* q)

{

assert(q);

return NULL == q->back;

}

// 销毁队列

void QueueDestroy(Queue* q)

{

assert(q);

QNode* cur = q->front;

while (cur)

{

q->front = cur->next;

free(cur);

cur = q->front;

}

q->front = NULL;

q->back = NULL;

}

// 栈的初始化

void StackInit(Stack* ps)

{

ps->array = (DataType*)malloc(sizeof(DataType) * 3);

if (NULL == ps->array)

{

assert(0);

printf("StackInit:malloc 申请空间失败！！！\n");

}

ps->size = 0;

ps->capacity = 3;

}

void CheckStackCapacity(Stack* ps)

{

assert(ps);

if (ps->size == ps->capacity)

{

// 1、开辟新空间

int newcapacity = ps->capacity * 2;

char* temp = malloc(sizeof(DataType) * newcapacity);

if (NULL == temp)

{

assert(0);

printf("CheckStackCapacity :malloc fail!!!\n");

}

// 2、转移旧空间

//void* memcpy(void* dest, const void* src, size_t count);

memcpy(temp, ps->array, sizeof(DataType) * ps->size);

// 3、释放旧空间

free(ps->array);

// 4、使用新空间

ps->array = temp;

ps->capacity = newcapacity;

}

// 入栈

void StackPush(Stack* ps, DataType data)

{

CheckStackCapacity(&ps);

ps->array[ps->size] = data;

ps->size++;

}

// 出栈

void StackPop(Stack* ps)

{

if (StackEmpty(ps))

{

return;

}

ps->size--;

}

// 获取栈顶元素

DataType Stacktop(Stack* ps)

{

assert(ps);

return ps->array[ps->size - 1];

}

// 获取栈中存放元素个数

int StackSize(Stack* ps)

{

assert(ps);

return ps->size;

}

// 检测栈中是否为空

int StackEmpty(Stack* ps)

{

assert(ps);

return 0 == ps->size;

}

// 销毁栈

void StackDestory(Stack* ps)

{

assert(ps);

free(ps->array);

ps->array = NULL;

ps->size = 0;

ps->capacity = 0;

}

//建立一个二叉树

BNode* BuyNode(char value)

{

BNode* newnode = (BNode*)malloc(sizeof(BNode));

newnode->m_value = value;

newnode->m_left = NULL;

newnode->m_right = NULL;

return newnode;

}

BNode* Create(char array[], int size, int* index)

{

BNode* root = NULL;

if ((*index) < size && array[*index] != '#')

{

root = BuyNode(array[*index]);

++(*index);

root->m_left = Create(array, size, index);

++(*index);

root->m_right = Create(array, size, index);

}

return root;

}

BNode* _Create(char array[], int size)

{

int index = 0;

return Create(array, size, &index);

}

// 递归遍历

// 先序（递归）遍历

void Preoder_Recursion(BNode* root)

{

if (root == NULL)

return;

printf("%c ", root->m_value);

Preoder_Recursion(root->m_left);

Preoder_Recursion(root->m_right);

}

// 中序（递归）遍历

void Inoder_Recursion(BNode* root)

{

if (root == NULL)

return;

Inoder_Recursion(root->m_left);

printf("%c ", root->m_value);

Inoder_Recursion(root->m_right);

}

// 中序（递归）遍历

void Postoder_Recursion(BNode* root)

{

if (root == NULL)

return;

Postoder_Recursion(root->m_left);

Postoder_Recursion(root->m_right);

printf("%c ", root->m_value);

}

///

// 层序遍历使用队列

void BinaryTreeLevelOrder(BNode* root)

{

Queue q;

QueueInit(&q);

QueuePush(&q, root);

while (!QueueEmpty(&q))

{

// a. 从队头取一个结点

BNode* cur = Queuefront(&q);

// b.遍历该结点

printf("%c ", cur->m_value);

// c. 如果cur有左孩子则入队列，有右孩子则入队列

if (cur->m_left)

QueuePush(&q, cur->m_left);

if (cur->m_right)

QueuePush(&q, cur->m_right);

// d. 遍历之后出队列

QueuePop(&q);

}

QueueDestroy(&q);

printf("\n");

}

// 非递归遍历

// 先序（非递归）遍历

void Preoder_Non_recursive(BNode* root)

{

Stack s;

StackInit(&s);

if (root == NULL)

return;

BNode* cur = NULL;

StackPush(&s, root); // 将根节点入栈

while (!StackEmpty(&s))

{

cur = Stacktop(&s); // cur指针每次指向栈顶元素

printf("%c ", cur->m_value); // 先序遍历根节点

StackPop(&s); // 遍历一次结点之后将该结点出栈

if (cur->m_right) // 先入栈根的右节点再入栈根的左结点

StackPush(&s, cur->m_right);

if (cur->m_left)

StackPush(&s, cur->m_left);

}

StackDestory(&s);

}

// 中序（非递归）遍历

void Inoder_Non_recursive(BNode* root)

{

Stack s;

StackInit(&s);

while (root != NULL || !StackEmpty(&s)) {

while (root != NULL) {

StackPush(&s, root);

root = root->m_left;

}

root = Stacktop(&s);

StackPop(&s);

printf("%c ", root->m_value);

root = root->m_right;

}

// 后序（非递归）遍历

void Postoder_Non_recursive(BNode* root)

{

Stack s;

StackInit(&s);

BNode* prev = NULL;

while (root || !StackEmpty(&s))

{

//循环每次迭代都是才开始访问树

while (root) // 左路节点入栈

{

StackPush(&s, root);

root = root->m_left;

} // 左路遇空

BNode* top = Stacktop(&s);

if (top->m_right == NULL || top->m_right == prev)

{

printf("%c ", top->m_value); // 后序遍历

prev = top; // 记录

StackPop(&s);

}

else

{

root = top->m_right; // 访问右路节点，再次进入循环继续遍历左路

}

// 二叉树节点个数

int BinaryTreeSize(BNode* root)

{

if (NULL == root)

return 0;

return 1 + BinaryTreeSize(root->m_left) + BinaryTreeSize(root->m_right);

}

// 二叉树的高度

int BinaryTreeHeight(BNode* root)

{

if (NULL == root)

return 0;

// 利用递归来求每个结点树的高度

// 先求左右子树的高度

// 返回高的那棵树+1

int left = BinaryTreeHeight(root->m_left);

int right = BinaryTreeHeight(root->m_right);

return left > right ? left + 1 : right + 1;

}

int main()

{

printf("请采用先序遍历输入数据\n");

char array[100] = { '#' };

gets_s(array, 99);

BNode* root = _Create(array, strlen(array));

printf("\n以下打印均采用递归方式\n");

printf("进行先序遍历打印输出\n");

Preoder_Recursion(root);

printf("\n");

printf("进行中序遍历打印输出\n");

Inoder_Recursion(root);

printf("\n");

printf("进行后序遍历打印输出\n");

Postoder_Recursion(root);

printf("\n");

printf("\n以下打印均采用非递归方式(使用栈)\n");

printf("进行先序遍历打印输出\n");

Preoder_Non_recursive(root);

printf("\n");

printf("进行中序遍历打印输出\n");

Inoder_Non_recursive(root);

printf("\n");

printf("进行后序遍历打印输出\n");

Postoder_Non_recursive(root);

printf("\n");

printf("\n进行层序遍历打印输出(使用队列)\n");

BinaryTreeLevelOrder(root);

printf("\n");

printf("该二叉树的结点个数为：%d\n", BinaryTreeSize(root));

printf("该二叉树的高度为：%d\n", BinaryTreeHeight(root));

printf("\n");

return 0;

}

5心得体会

对于非递归算法，我使用了栈结构和队列结构，分别用于前序遍历、中序、后序遍历、非递归层次序遍历方法中。使用栈和队列的过程中，我在实践中又学习了栈和队列的一些知识，提

高了各种逻辑结构之间的综合运用能力。通过这次课程设计，我发现，知识不仅仅是在课本上，多查阅一些资料能够更好的完成课题，并且，只有把书本上的知识实际应用下来，才能把知识学到融会贯通，而且学习过程中一定不要怕繁琐，调试过程中一定会遇到一些难以解决的问题，这个时候我需要和老师和同学去请教，还有慢慢耐心地调试，才可以。

源码（点个小赞呗）

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
//建立一个二叉树，并对其进行4种遍历(前中后层)。
//[要求] 使用递归和非递归，计算二叉树中节点的个数，树的深度。
// 使用c语言

// 树结构体
typedef struct _BNode
{
	char m_value;
	struct _BNode* m_left;
	struct _BNode* m_right;
}BNode;

// 存放树结点的栈结构体
typedef struct BNode* DataType;
typedef struct _Stack
{
	DataType* array;
	int capacity;
	int size;
}Stack;

// 存放树结点的队列结构体
typedef struct BNode* QDataType;
typedef struct QNode
{
	QDataType data;			//结点结构体的定义
	struct QNode* next;		//结点中保存着数据域与指针域
}QNode;
typedef struct Queue
{
	struct QNode* front;	// 队列结构体中
	struct QNode* back;		// 存放着标记队列队头与队尾的两个指针
}Queue;


QNode* QueueBuyNode(QDataType data)
{
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (NULL == newnode)
	{
		assert(0);
		printf("BuyNode !!!\n");
	}
	newnode->data = data;
	newnode->next = NULL;
	return newnode;
}

// 初始化队列
void QueueInit(Queue* q)
{
	assert(q);
	q->back = NULL;
	q->front = NULL;
}

// 队尾入队列
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	// 0、创建一个新结点进行尾插
	QNode* newnode = QueueBuyNode(data);

	// 1、队列中没有结点
	if (QueueEmpty(q))
	{
		q->front = newnode;
		q->back = newnode;
	}
	else
	{
		// 2、队列中有结点
		q->back->next = newnode;
		q->back = newnode;
	}
}

// 队头出队列
void QueuePop(Queue* q)
{
	assert(q);
	// 1、队列中没有元素
	if (QueueEmpty(q))
		return;

	// 2、队列中只有一个元素
	else if (q->back == q->front)
	{
		free(q->front);
		q->front = NULL;
		q->back = NULL;
	}

	// 3、队列中有多个元素
	else
	{
		QNode* del = q->front;
		q->front = del->next;
		free(del);
	}
}

// 获取队列头部元素
QDataType Queuefront(Queue* q)
{
	assert(q);
	return q->front->data;
}

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	return NULL == q->back;
}

// 销毁队列
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* cur = q->front;
	while (cur)
	{
		q->front = cur->next;
		free(cur);
		cur = q->front;
	}
	q->front = NULL;
	q->back = NULL;
}

// 栈的初始化
void StackInit(Stack* ps)
{
	ps->array = (DataType*)malloc(sizeof(DataType) * 3);
	if (NULL == ps->array)
	{
		assert(0);
		printf("StackInit:malloc 申请空间失败！！！\n");
	}
	ps->size = 0;
	ps->capacity = 3;
}

void CheckStackCapacity(Stack* ps)
{
	assert(ps);
	if (ps->size == ps->capacity)
	{
		// 1、开辟新空间
		int newcapacity = ps->capacity * 2;
		char* temp = malloc(sizeof(DataType) * newcapacity);
		if (NULL == temp)
		{
			assert(0);
			printf("CheckStackCapacity :malloc fail!!!\n");
		}

		// 2、转移旧空间
		//void* memcpy(void* dest, const void* src, size_t count);
		memcpy(temp, ps->array, sizeof(DataType) * ps->size);

		// 3、释放旧空间
		free(ps->array);

		// 4、使用新空间
		ps->array = temp;
		ps->capacity = newcapacity;
	}
}

// 入栈
void StackPush(Stack* ps, DataType data)
{
	CheckStackCapacity(&ps);
	ps->array[ps->size] = data;
	ps->size++;
}

// 出栈
void StackPop(Stack* ps)
{
	if (StackEmpty(ps))
	{
		return;
	}
	ps->size--;
}

// 获取栈顶元素
DataType Stacktop(Stack* ps)
{
	assert(ps);
	return ps->array[ps->size - 1];
}

// 获取栈中存放元素个数
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->size;
}

// 检测栈中是否为空
int StackEmpty(Stack* ps)
{
	assert(ps);
	return 0 == ps->size;
}

// 销毁栈
void StackDestory(Stack* ps)
{
	assert(ps);
	free(ps->array);
	ps->array = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

//建立一个二叉树
BNode* BuyNode(char value)
{
	BNode* newnode = (BNode*)malloc(sizeof(BNode));
	newnode->m_value = value;
	newnode->m_left = NULL;
	newnode->m_right = NULL;
	return newnode;
}
BNode* Create(char array[], int size, int* index)
{
	BNode* root = NULL;
	if ((*index) < size && array[*index] != '#')
	{
		root = BuyNode(array[*index]);
		++(*index);
		root->m_left = Create(array, size, index);
		++(*index);
		root->m_right = Create(array, size, index);
	}
	return root;
}

BNode* _Create(char array[], int size)
{
	int index = 0;
	return Create(array, size, &index);
}

// 递归遍历

// 先序（递归）遍历
void Preoder_Recursion(BNode* root)
{
	if (root == NULL)
		return;
	printf("%c ", root->m_value);
	Preoder_Recursion(root->m_left);
	Preoder_Recursion(root->m_right);
}
// 中序（递归）遍历
void Inoder_Recursion(BNode* root)
{
	if (root == NULL)
		return;
	Inoder_Recursion(root->m_left);
	printf("%c ", root->m_value);
	Inoder_Recursion(root->m_right);
}
// 中序（递归）遍历
void Postoder_Recursion(BNode* root)
{
	if (root == NULL)
		return;
	Postoder_Recursion(root->m_left);
	Postoder_Recursion(root->m_right);
	printf("%c ", root->m_value);
}

///
// 层序遍历 使用队列
void BinaryTreeLevelOrder(BNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		// a. 从队头取一个结点 
		BNode* cur = Queuefront(&q);
		// b.遍历该结点
		printf("%c ", cur->m_value);

		// c. 如果cur有左孩子则入队列，有右孩子则入队列
		if (cur->m_left)
			QueuePush(&q, cur->m_left);
		if (cur->m_right)
			QueuePush(&q, cur->m_right);
		// d. 遍历之后出队列
		QueuePop(&q);
	}
	QueueDestroy(&q);
	printf("\n");
}

// 非递归遍历

// 先序（非递归）遍历
void Preoder_Non_recursive(BNode* root)
{
	Stack s;
	StackInit(&s);
	if (root == NULL)
		return;
	BNode* cur = NULL;
	StackPush(&s, root);			// 将根节点入栈
	while (!StackEmpty(&s))
	{
		cur = Stacktop(&s);		// cur指针每次指向栈顶元素
		printf("%c ", cur->m_value);	// 先序遍历根节点
		StackPop(&s);	// 遍历一次结点之后将该结点出栈		
		if (cur->m_right)				// 先入栈根的右节点再入栈根的左结点
			StackPush(&s, cur->m_right);
		if (cur->m_left)
			StackPush(&s, cur->m_left);
	}
	StackDestory(&s);
}
// 中序（非递归）遍历
void Inoder_Non_recursive(BNode* root)
{
	Stack s;
	StackInit(&s);
	while (root != NULL || !StackEmpty(&s)) {
		while (root != NULL) {
			StackPush(&s, root);
			root = root->m_left;
		}
		root = Stacktop(&s);
		StackPop(&s);
		printf("%c ", root->m_value);
		root = root->m_right;
	}
}
// 后序（非递归）遍历
void Postoder_Non_recursive(BNode* root)
{
	Stack s;
	StackInit(&s);
	BNode* prev = NULL;
	while (root || !StackEmpty(&s))
	{
		//循环每次迭代都是才开始访问树
		while (root) // 左路节点入栈
		{
			StackPush(&s, root);
			root = root->m_left;
		} // 左路遇空

		BNode* top = Stacktop(&s);

		if (top->m_right == NULL || top->m_right == prev)
		{
			printf("%c ", top->m_value); // 后序遍历
			prev = top; // 记录
			StackPop(&s);
		}
		else
		{
			root = top->m_right; // 访问右路节点，再次进入循环继续遍历左路
		}
	}
}
// 二叉树节点个数
int BinaryTreeSize(BNode* root)
{
	if (NULL == root)
		return 0;
	return 1 + BinaryTreeSize(root->m_left) + BinaryTreeSize(root->m_right);
}

// 二叉树的高度
int BinaryTreeHeight(BNode* root)
{
	if (NULL == root)
		return 0;

	// 利用递归来求每个结点树的高度
	// 先求左右子树的高度
	// 返回高的那棵树+1
	int left = BinaryTreeHeight(root->m_left);
	int right = BinaryTreeHeight(root->m_right);
	return left > right ? left + 1 : right + 1;
}

int main()
{
	printf("请采用先序遍历输入数据\n");
	char array[100] = { '#' };
	gets_s(array, 99);
	BNode* root = _Create(array, strlen(array));
	printf("\n以下打印均采用递归方式\n");
	printf("进行先序遍历打印输出\n");
	Preoder_Recursion(root);
	printf("\n");

	printf("进行中序遍历打印输出\n");
	Inoder_Recursion(root);
	printf("\n");

	printf("进行后序遍历打印输出\n");
	Postoder_Recursion(root);
	printf("\n");

	printf("\n以下打印均采用非递归方式(使用栈)\n");
	printf("进行先序遍历打印输出\n");
	Preoder_Non_recursive(root);
	printf("\n");

	printf("进行中序遍历打印输出\n");
	Inoder_Non_recursive(root);
	printf("\n");

	printf("进行后序遍历打印输出\n");
	Postoder_Non_recursive(root);
	printf("\n");

	printf("\n进行层序遍历打印输出(使用队列)\n");
	BinaryTreeLevelOrder(root);
	printf("\n");

	printf("该二叉树的结点个数为：%d\n", BinaryTreeSize(root));
	printf("该二叉树的高度为：%d\n", BinaryTreeHeight(root));
	printf("\n");
	return 0;
}