传统ICP存在匹配速度慢，误匹配率高等缺点。

粗配准是在不清楚两个点云的相对位置的情况下，找到这两个点云近似的旋转平移矩阵，主要是为精配准提供初始变换矩阵；精配准在已知旋转平移矩阵的情况下，通过多次迭代优化进一步得到更加精确的旋转平移矩阵

已知两个代配准点云P和Q，匹配两点云中欧氏距离最近的点来获取变换矩阵，通过不断迭代，，来得到最优变换矩阵。

（1）首先一点，ICP算法在进行点云精配准时需要一个初始的点云位置，需要初始点云和配准点云在同一坐标系下，如果两个待配点云欧式距离较远，会造成匹配错误，影响最终匹配效果。
（2）一般实际应用中，需要两配准点云仅仅是部分重叠关系，而ICP算法无法确保两点云的重叠区域，会造成误匹配问题。
（3）ICP算法进行点云配准时需要将所有的点云进行查找匹配，如果点云个数较多，那查找时间会较长，严重影响配准效率。

解决问题（自动获取初值、提高配准效率）。

点云数据能够以较小的存储成本获得物体准确的拓扑结构和几何结构，因而获得越来越广泛的关注。在实际的采集过程中，因为被测物体尺寸过大，物体表面被遮挡或者三维扫描设备的扫描角度等因素，单次的扫描往往得不到物体完整的几何信息。因此，为了获得被测物体的完整几何信息，就需要将不同视角即不同参考坐标下的两组或者多组点云统一到统一坐标系下，进行点云的配准。
（1）刚性变换矩阵

点云配准的最终目的是通过一定的旋转和平移变换将不同坐标系下的两组或者多组点云数据统一到同一参考坐标系下。这个过程，可以通过一组映射来完成。假设映射变换为H，这H可以用以下的公式来表示。

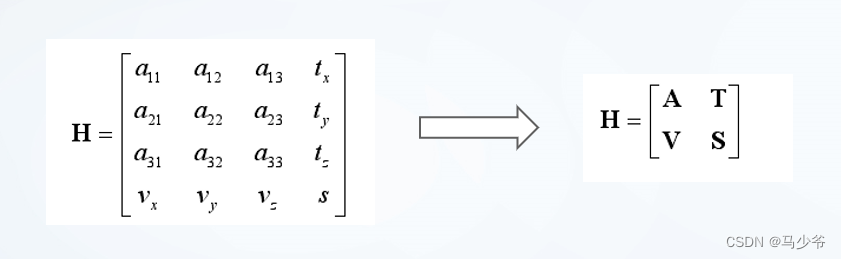
其中A代表旋转矩阵，T代表平移向量，V代表透视变换向量，S代表整体的比例因子。因为根据一系列图片得到的点云数据只存在旋转和平移变换，不存在形变，所以将V设为零向量，比例因子S=1。

映射变换H可以表示为：

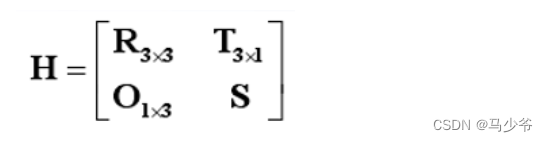
其中，旋转矩阵R3X3和平移矩阵T3X1可以通过以下公式来表示：

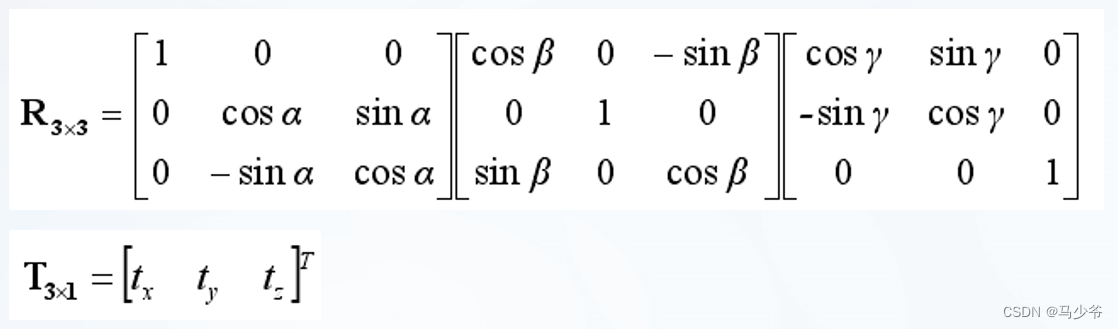
其中α、β、γ分别表示点沿x、y、z轴的旋转角度，tx、ty、tz分别表示点沿x、y、z轴的平移量。

（2）刚性变换矩阵的参数估计

将两个不同坐标系下的点 X和X’进行坐标变换时，可以通过以下公式来实现转换：


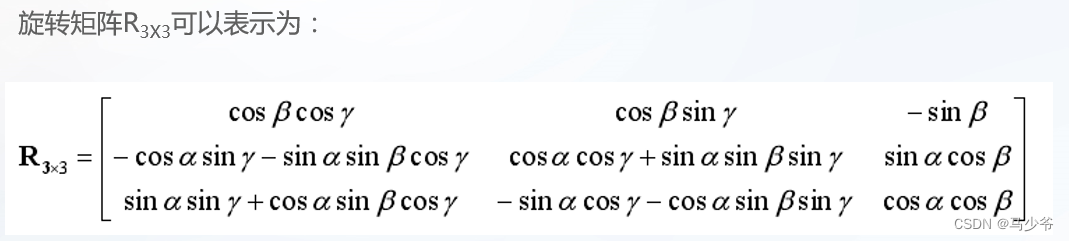
刚性变换矩阵中涉及到六个未知数α、β、γ、 tx、ty、tz。要唯一确定这六个未知参数，需要六个线性方程，即至少需要在待匹配点云重叠区域找到3组对应点对，且3组对应点对不能共线，才可以得到这几个未知数的值，进而完成刚性矩阵的参数估计。通常情况下，人们会选择尽可能多的对应点对，进一步提高刚性变换矩阵的参数估计精度。

在待匹配的两组点云数据的重叠区域内，分别选取两个点集来表示源点集和目标点集，其中P={pi|pi∈R3，i=1,2，……n}为源点集，Q ={qj|qj∈R3，j=1,2，……m}为目标点集，m和n分别代码两个点集的规模。设旋转矩阵为R，平移矩阵为t，用f（R，t）来表示源点集P在变换矩阵（R，t）下与目标点集Q之间的误差。则求解最优变换矩阵的问题就可以转化为求满足min（f（R，t））的最优解（R，t）。

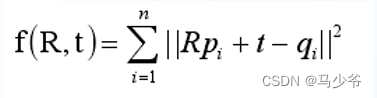
ICP:





以三组对应点为例：

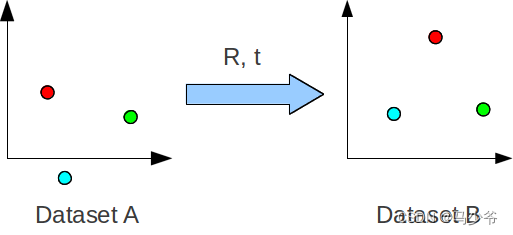
对应点的颜色相同，R是旋转，t是平移。我们想要找到将数据集A中的点与数据集b对齐的最佳旋转和平移。这种变换有时被称为欧几里德变换或刚性变换，因为它保持了形状和大小。这与仿射变换形成对比，仿射变换包括缩放和剪切。

我将给出的解决方案来自于Besl和McKay在1992年发表的论文:
“A Method for Registration of 3-D Shapes’, by Besl and McKay, 1992.”

解决方案概述
我们正在求解方程中的R,t:
B = R*A + t，
其中R,t是应用于数据集A的变换，使其与数据集B尽可能对齐。求最优刚性变换矩阵可分解为以下步骤:
1.求两个数据集的质心
2.将两个数据集带到原点，然后求最优旋转(矩阵R)
3.求平移t

求质心
求质心这一点很简单，质心只是平均点，可以计算如下：

求最优旋转
有几种方法可以找到点之间的最佳旋转。我发现最简单的方法是使用奇异值分解(SVD)，

为了找到最佳的旋转，我们首先将两个数据集重新居中，使两个中心点都位于原点，如下图所示。

H是协方差矩阵。
特殊情况

if determinant(R) < 0
  multiply 3rd column of V by -1
  recompute R
end if

An alternative check that is possibly more robust was suggested by Nick Lambert, where R is the rotation matrix.

if determinant(R) < 0
  multiply 3rd column of R by -1
end if

% This function finds the optimal Rigid/Euclidean transform in 3D space
% It expects as input a Nx3 matrix of 3D points.
% It returns R, t

% You can verify the correctness of the function by copying and pasting these commands:
%{

R = orth(rand(3,3)); % random rotation matrix

if det(R) < 0
    V(:,3) *= -1;
    R = V*U';
end

t = rand(3,1); % random translation

n = 10; % number of points
A = rand(n,3);
B = R*A' + repmat(t, 1, n);
B = B';

[ret_R, ret_t] = rigid_transform_3D(A, B);

A2 = (ret_R*A') + repmat(ret_t, 1, n)
A2 = A2'

% Find the error
err = A2 - B;
err = err .* err;
err = sum(err(:));
rmse = sqrt(err/n);

disp(sprintf("RMSE: %f", rmse));
disp("If RMSE is near zero, the function is correct!");

%}

% expects row data
function [R,t] = rigid_transform_3D(A, B)
    if nargin != 2
	    error("Missing parameters");
    end

    assert(size(A) == size(B))

    centroid_A = mean(A);
    centroid_B = mean(B);

    N = size(A,1);

    H = (A - repmat(centroid_A, N, 1))' * (B - repmat(centroid_B, N, 1));

    [U,S,V] = svd(H);

    R = V*U';

    if det(R) < 0
        printf("Reflection detected\n");
        V(:,3) = -1*V(:,3);
        R = V*U';
    end

    t = -R*centroid_A' + centroid_B'
end

 centroid_A = mean(A);
 centroid_B = mean(B);

  N = size(A,1);

  H = (A - repmat(centroid_A, N, 1))' * (B - repmat(centroid_B, N, 1));

  A_move=A - repmat(centroid_A, N, 1);
  B_move=B - repmat(centroid_B, N, 1);

  A_norm=sum(A_move.*A_move,2);
  B_norm=sum(B_move.*B_move,2);

  %计算尺度平均值
  lam2=A_norm./B_norm;
  lam2=mean(lam2);

  [U,S,V] = svd(H);
  R = V*U';

  if det(R) < 0
  printf('Reflection detected\n');
  V(:,3) = -1*V(:,3);
  R = V*U';
  end
  %计算最终的旋转矩阵与平移向量
  t = -R./(lam2^(0.5))*centroid_A' + centroid_B';
  R = R./(lam2^(0.5));
  end

ret_R =

0.7611    0.6455    0.0636

-0.0433 -0.0474 0.9979
0.6472 -0.7623 -0.0081

ret_t =

364.4787
9.8487
-255.8585

正常迭代要151次

迭代次数ieration=151
误差err=14.9144
旋转矩阵T=
   -0.9995   -0.0257   -0.0197  163.4968
    0.0214   -0.0682   -0.9974 -335.4744
   -0.0243    0.9973   -0.0688  -18.2146
         0         0         0    1.0000

首先选择三组对应点进行粗配准

A = load('CAD1.txt')%CAD点云

B = load('PC1.txt')%采集点云

[n,m] = size(A)

[ret_R, ret_t] = rigid_transform_3D(A, B)
A2 = (ret_R*A') + repmat(ret_t, 1, n)
A2 = A2'

% Find the error
err = A2 - B;
err = err .* err;
err = sum(err(:));
rmse = sqrt(err/n);

disp(sprintf('RMSE: %f', rmse));
disp('If RMSE is near zero, the function is correct!');

旋转矩阵获取:

ret_R =

    0.9999   -0.0145   -0.0010
   -0.0010   -0.0016   -1.0000
    0.0145    0.9999   -0.0016


ret_t =

  -94.8635
 -327.7857
  -28.8730

然后给ICP作为初值
只需要迭代73次

迭代次数ieration=73
误差err=13.6329
旋转矩阵T=
    0.9998   -0.0163   -0.0129  -93.9838
   -0.0139   -0.0620   -0.9980 -329.5601
    0.0155    0.9979   -0.0622  -23.1826
         0         0         0    1.0000