活动 - AcWing

acw1137

如果我们确定了起点，那么就是一个模板题

选起点有两个办法：1.选取虚拟原点，连接家附近的所有车站。直接以虚拟原点作为我起点跑最短路即可。2.反向建图，取终点到家附近所有车站的dist，取min即可。 

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N =1010,M=20010,INF=0x3f3f3f3f;

int n,m,T;
int h[N],e[M],ne[M],w[M],idx;
int dist[N],q[N];
bool st[N];
//虚拟原点连家附近的车站  或者反向建图
void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

void spfa()
{
    int scnt;
    cin>>scnt;
    memset(dist,0x3f,sizeof dist);
    int hh=0,tt=0;
    while(scnt--)
    {
        int u;
        cin>>u;
        dist[u]=0;
        q[tt++]=u;
        st[u]=true;
    }

    while(hh!=tt)
    {
        int t=q[hh++];
        if(hh==N) hh=0;

        st[t]=false;
        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+w[i])
            {
                dist[j]=dist[t]+w[i];
                if(!st[j])
                {
                    q[tt++]=j;
                    if(tt==N) tt=0;
                    st[j]=true; 
                }

            }
        }
    }
}


int main()
{
    while(scanf("%d%d%d",&n,&m,&T)!=-1)
    {
        memset(h,-1,sizeof h);
        idx=0;
        while(m--)
        {
            int a,b,c;
            cin>>a>>b>>c;
            add(a,b,c);
        }
        spfa();
        if(dist[T]==INF) dist[T]=-1;
        cout<<dist[T]<<endl;
    }
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4338580/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

acw1131

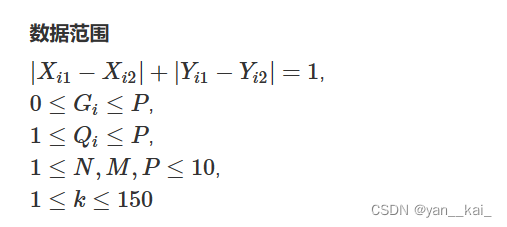
思路1：

来自：AcWing 1131. 拯救大兵瑞恩（普通BFS解决） - AcWing 

在直接bfs可做的基础上，引入了“钥匙”和门这个因素。可以想到暴力做法，直接在状态中加入“持有钥匙”这一维度，现在题目就转化为了从状态f[1][0]转化为f[n*m][…]状态的最小步数了。

我们走到有钥匙的格子上，并不用考虑要不要拿钥匙，拿钥匙又不会增加成本，只管拿就行。因此，转移到某个格子时，直接计算下这个格子的状态，格子上有钥匙就在之前状态基础上加上这个钥匙，没有钥匙就继承之前的钥匙状态。这样一来，问题中就不存在边权为0的边了，只要状态转移了，步长都是加一，普通的BFS就可以解决了。

细节：二维坐标压缩成一个数，这样可以g[a][b]表示a到b之间的边了。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int N =105,M=12;
typedef pair<int,int> PII;

int g[N][N],key[N],dist[N][1<<M];
bool st[N][1<<M];
int n,m,p,k,s;

int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};


int get(int x,int y)//坐标的状态压缩
{
    return (x-1)*m+y;
}


int bfs()
{
    queue<PII> q;
    q.push({1,key[1]});
    st[1][key[1]]=true;
    memset(dist,0x3f,sizeof dist);
    dist[1][key[1]]=0;
    
    while(q.size())
    {
        auto t=q.front();
        q.pop();
        int ver=t.first,state=t.second;
        int x=(ver-1)/m+1,y=(ver-1)%m+1;
        
        
        for(int i=0;i<4;i++)
        {
            int a=x+dx[i],b=y+dy[i];
            int s=state,p=get(a,b);
            if(!a||!b||a>n||b>m||!g[ver][p]) continue;
            if(g[ver][p]!=-1)
                if(!(s>>g[ver][p]&1)) continue;
            
            s|=key[p];
            if(!st[p][s])
            {
                q.push({p,s});
                st[p][s]=true;
                dist[p][s]=dist[ver][state]+1;
            }
            if(p==n*m) return dist[p][s];
            
        }
    }
    return -1;
}


int main()
{
    cin>>n>>m>>p;
    cin>>k;
    memset(g,-1,sizeof g);
    for(int i=0;i<k;i++)
    {
        int x1,y1,x2,y2,z;
        cin>>x1>>y1>>x2>>y2>>z;
        int p1=get(x1,y1),p2=get(x2,y2);
        g[p1][p2]=g[p2][p1]=z;
    }
    
    cin>>s;
    for(int i=0;i<s;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        key[get(x,y)] |= 1<<z;
    }
    cout<<bfs()<<endl;
}

思路2：

 

 

把捡钥匙看做一次移动，边权为0。格子间的移动视为一次移动，边权是1，然后使用双端队列bfs。线性复杂度。

小结：

思考图论问题有时候和dp十分相似。思考问题前，我们可以先把图假设为拓扑图，然后思考可行的dp方式，如状态表示和状态转移。

但是实际上图是可能存在环的，因此直接dp这种线性的方式不可行，但是可以借助图论算法框架来处理。某些图论算法还具有拓扑图性质。后续还会数次讲到类似思想。 

acwing1134最短路计数

首先用dp的方式思思考一下：

如果我们要计算i点的最短路方案，集合可以按照从哪个点转移到i点来划分。状态计算也非常简单，，，设i点可以由k1，k2，，kn点转移过去。则状态转移方程为：if(dist(ki)+w(i)==dist(i) cnt(i)+=cnt(ki)。  

为此，我们要知道所有ki点的最短路dist。我们发现一个性质，当我们要求状态state的时，状态集合里的所有值我们需要事先知道。这就是一个拓扑性质。要在计算最短路时统计方案数，则要求具备拓扑性质（最短路树），那么跑哪个算法满足我们的要求呢？

 抽象成拓扑图：跑一遍可以跑出最短路树，无环。判断方式：求解每个点的dist不互相依赖。

BFS 只入队一次，出队一次。可以抽象成拓扑图， 因为它可以保证被更新的点的父节点一定已经是最短距离了，并且这个点的条数已经被完全更新过了。这个性质是核心性质。
dijkstra 每个点只出队一次。也可以抽象成拓扑图， 同理由于每一个出队的点一定已经是最短距离，并且它出队的时候是队列中距离最小的点，这就代表他的最短距离条数已经被完全更新了，所以构成拓扑性质。
bellman_ford算法 spfa 本身不具备拓扑序，因为更新它的点不一定是最短距离，所以会出错。

当然spfa是可以做的，不过需要先把最短路，再统计方案。 

#include<iostream>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;

const int N =100010,M=400010,mod=100003;

int h[N],e[M],ne[M],idx;
int n,m;
int dist[N],cnt[N];

void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void bfs()
{
    memset(dist,0x3f,sizeof dist);
    queue<int> q;
    q.push(1);

    cnt[1]=1;
    dist[1]=0;

    while(q.size())
    {
        int t=q.front();
        q.pop();

        for(int i=h[t];i!=-1;i=ne[i])
        {
            int j=e[i];
            if(dist[j]>dist[t]+1)
            {
                dist[j]=dist[t]+1;
                q.push(j);
                cnt[j]=cnt[t];
            }
            else if(dist[j]==dist[t]+1)
            {
                cnt[j]=(cnt[j]+cnt[t])%mod;
            }

        }
    }

}


int main()
{
    cin>>n>>m;
    memset(h,-1,sizeof h);
    for(int i=0;i<m;i++)
    {
        int a,b;
        cin>>a>>b;
        add(a,b),add(b,a);
    }

    bfs();
    for(int i=1;i<=n;i++) cout<<cnt[i]<<endl;
    return 0;


}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4340742/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

acwing383 单源次最短路

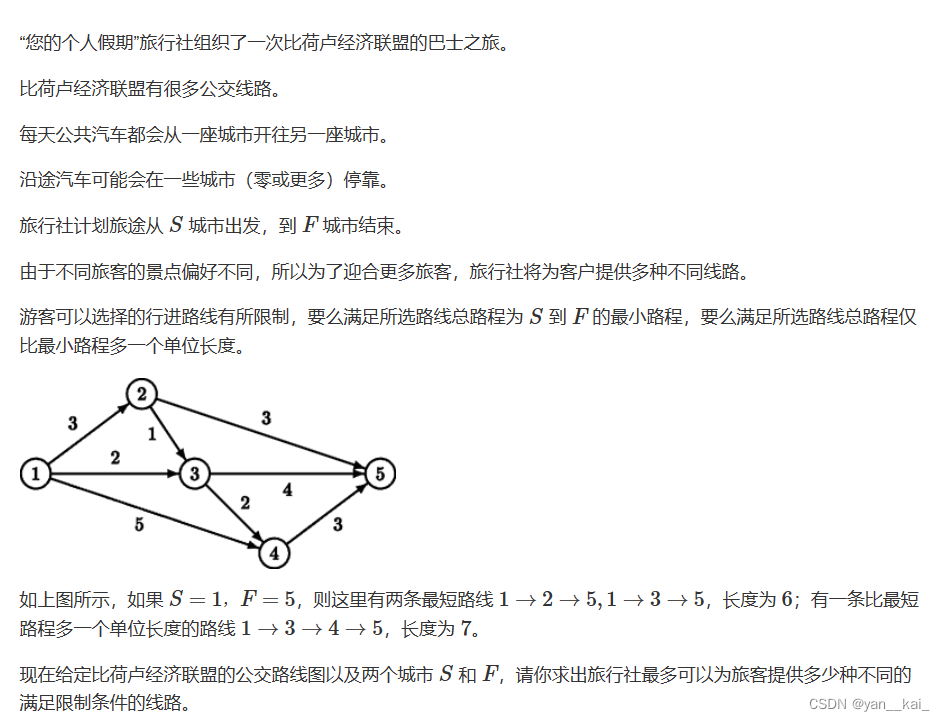
 本题就是上一题的拓展，即统计次短路条数。如果次短路比最短路多1，则答案加上次短路条数。

同理可知，求次短路，bfs和dijkstra仍然具有拓扑性质。因为不可能存在环形依赖，一个点不可能反回去更新前一个点的次短路（因为这样次短路就会变长，显然是不可能的）。因此可以边算最短路、次短路，边统计最短路和次短路的方案。

结合第2道题，我们需要加入一维状态表示最短，次短。

状态转移：初始状态：最短路为0，没有次短路。最短路方案为1，没有次短路方案。

计算：如果新路dist比最短路小，最短路更新放入堆中继续搜，原最短路沦为次短路，次短路被更新，放入堆中继续搜。

如果与最短一样大，统计方案

如果比次短小，比最短大，更新次短

如果和次短一样大，收钱。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;

const int N =1010,M=20010;

struct Ver{
    int id,type,dist;
    bool operator> (const Ver &W) const
    {
        return dist > W.dist;
    }
};
int h[N],e[M],ne[M],w[M],idx;
int n,m,S,T;
int cnt[N][2],dist[N][2];
bool st[N][2];

void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

int dijkstra()
{
    memset(cnt,0,sizeof cnt);
    memset(st,false,sizeof st);
    memset(dist,0x3f,sizeof dist);

    dist[S][0]=0,cnt[S][0]=1;
    priority_queue<Ver, vector<Ver>, greater<Ver> > heap;
    heap.push({S,0,0});

    while(heap.size())
    {
        auto t=heap.top();
        heap.pop();
        int ver=t.id,type=t.type,distance=t.dist,count=cnt[ver][type];

        if(st[ver][type]) continue;
        st[ver][type]=true;
        for(int i=h[ver];~i;i=ne[i])
        {
            int j=e[i];
            if(dist[j][0]>distance+w[i])
            {
                dist[j][1]=dist[j][0];
                cnt[j][1]=cnt[j][0];
                heap.push({j,1,dist[j][1]});
                dist[j][0]=distance+w[i];
                cnt[j][0]=count;
                heap.push({j,0,dist[j][0]});
            }
            else if(dist[j][0]==distance+w[i]) cnt[j][0]+=count;
            else if(dist[j][1]>distance+w[i]) 
            {
                dist[j][1]=distance+w[i];
                cnt[j][1]=count;
                heap.push({j,1,dist[j][1]});
            }
            else if(dist[j][1]==distance+w[i]) cnt[j][1]+=count;
        }
    }

    int res=cnt[T][0];
    if(dist[T][1]==dist[T][0]+1) res+=cnt[T][1];

    return res;
}


int main()
{
    int cases;
    cin>>cases;
    while(cases--)
    {
        scanf("%d%d",&n,&m);
        memset(h,-1,sizeof h);
        idx=0;

        while(m--)
        {
            int a,b,c;
            cin>>a>>b>>c;
            add(a,b,c);
        }
        scanf("%d%d",&S,&T);
        cout<<dijkstra()<<endl;
    }
    return 0;
}


作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4372015/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。