题目所属分类
动态规划 前面写过一个面积最大的长方形
传送门
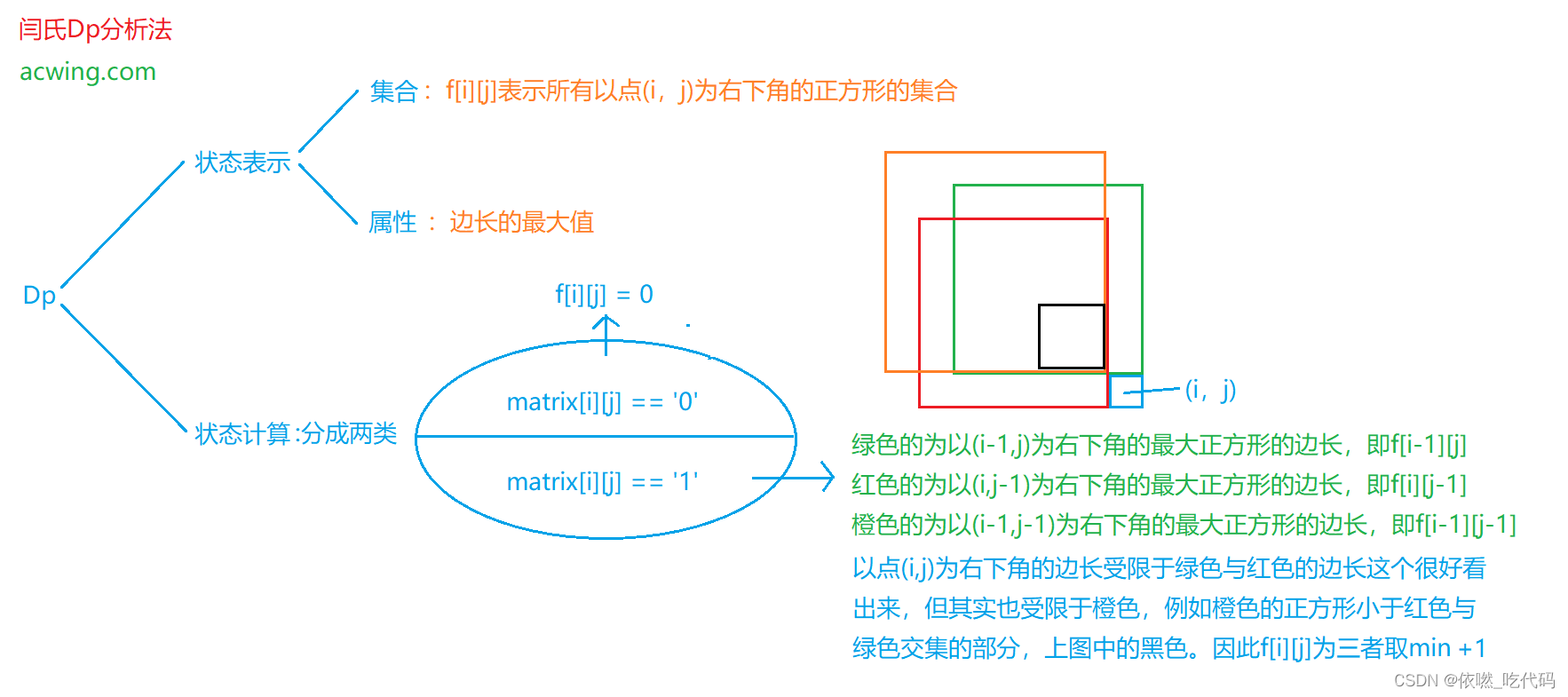
f[i, j]表示:所有以(i,j)为右下角的且只包含 1`` 的正方形的边长最大值
原题链接
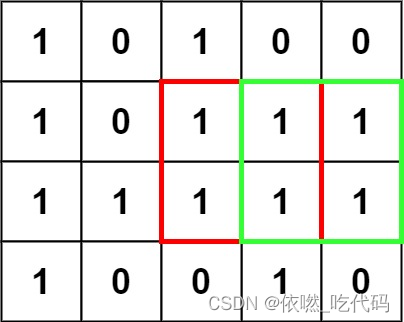
在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。
代码案例:
输入:matrix = [[“1”,“0”,“1”,“0”,“0”],[“1”,“0”,“1”,“1”,“1”],[“1”,“1”,“1”,“1”,“1”],[“1”,“0”,“0”,“1”,“0”]]
输出:4
题解
状态计算
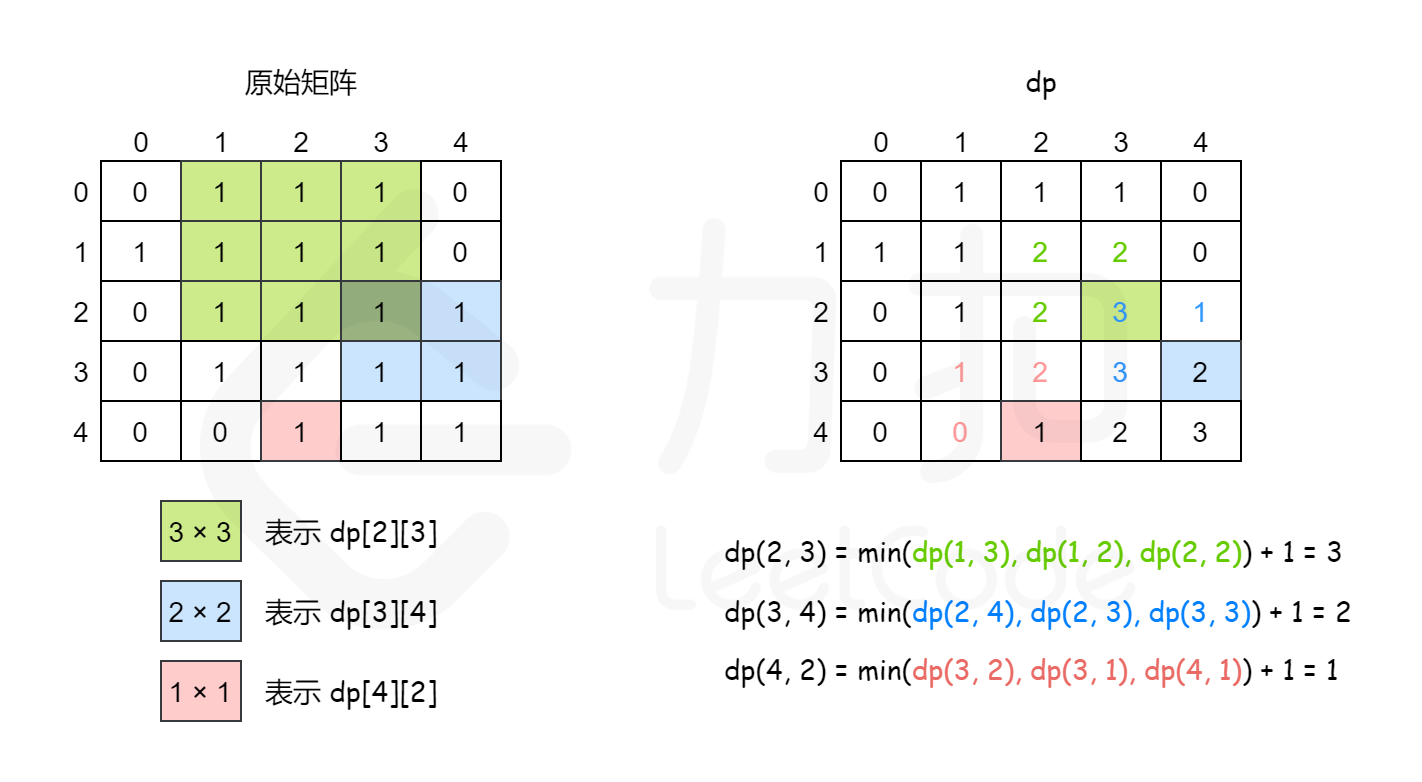
如果该位置的值是 0,则 f[i, j] = 0,因为当前位置不可能在由 1 组成的正方形中
如果该位置的值是 1,则 f[i, j]的值由其上方、左方和左上方的三个相邻位置的状态值决定。具体而言,当前位置的元素值等于三个相邻位置的元素中的最小值加 1,状态转移方程如下:
f[i,j]=min(f[i−1,j−1],f[i−1,j],f[i,j−1])+1
为什么要三者取最小+1 ?
有个题解解释得也很清楚,继续搬运
若形成正方形(非单 1),以当前为右下角的视角看,则需要:当前格、上、左、左上都是 1
可以换个角度:当前格、上、左、左上都不能受 0 的限制,才能成为正方形
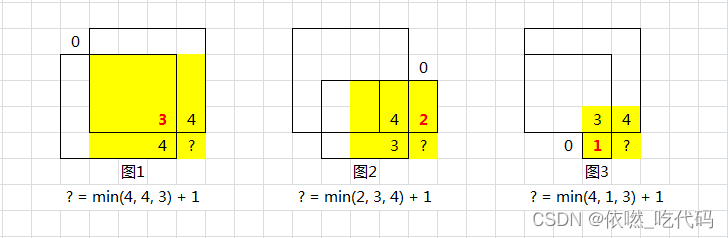
上面详解了 三者取最小 的含义:
图 1:受限于左上的 0
图 2:受限于上边的 0
图 3:受限于左边的 0
数字表示:以此为正方形右下角的最大边长
黄色表示:格子 ? 作为右下角的正方形区域
就像 木桶的短板理论 那样——附近的最小边长,才与 ? 的最长边长有关。
class Solution {
public int maximalSquare(char[][] matrix) {
int n = matrix.length ;
int m = matrix[0].length ;
int[][] f = new int[n+10][m+10];
int res = 0 ;
for(int i = 1 ; i <= n ; i ++){
for(int j = 1 ; j <= m ; j++){
if(matrix[i-1][j-1] == '1'){
f[i][j] = Math.min(f[i-1][j],Math.min(f[i][j-1],f[i-1][j-1]))+1 ;
res = Math.max(res,f[i][j]);
}
}
}
return res*res ;
}
}