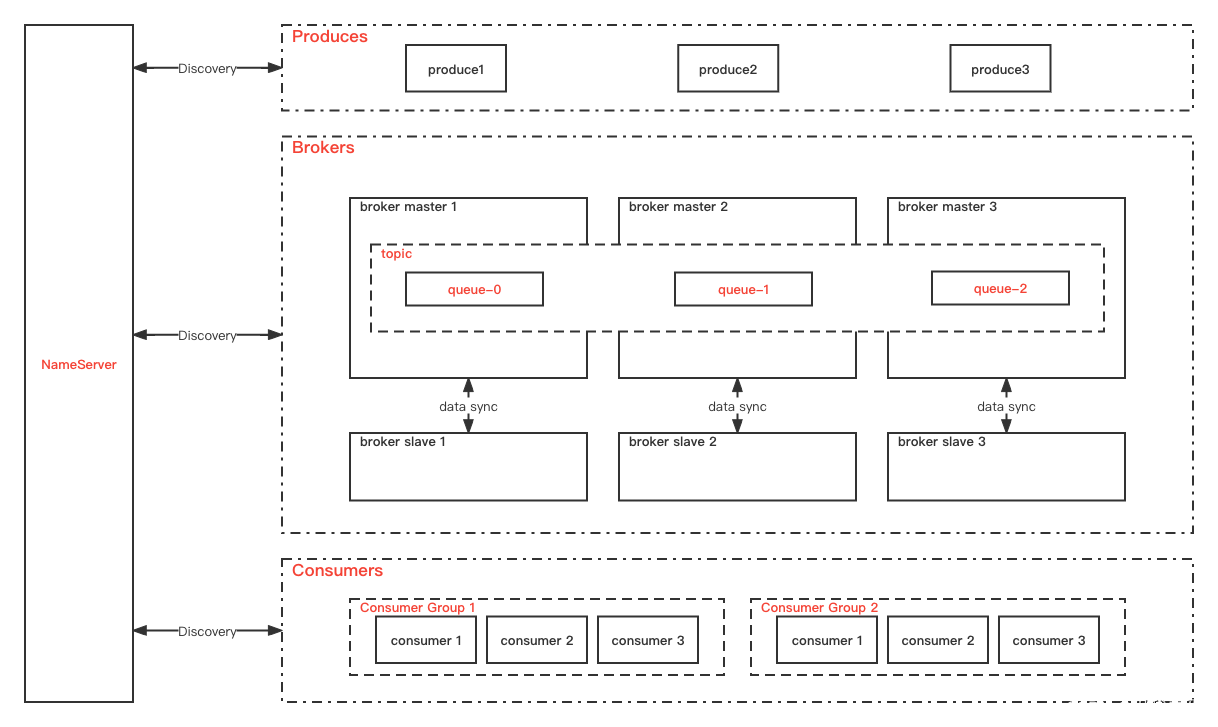
树形dp
文章目录
- 树形dp
- 概述
- 树形dp + 路径问题
- 树的最长路径
- 思路
- 代码
- 树的中心
- 换根DP
- 思路
- 代码
- 数字转换
- 思路
- 代码
- 树形dp + 有依赖的背包
- 二叉苹果树
- 思路
- 代码
- 树形dp + 状态机
- 没有上司的舞会
- 思路
- 代码
- 战略游戏
- 思路
- 代码
- 皇宫看守
- 思路
- 代码
- 总结
概述
树形 DP,即在树上进行的 DP。由于树固有的递归性质,树形 DP 一般都是递归进行的。
在树上设计动态规划算法时,一般就以节点从深到浅(子树从小到大)的顺序作为DP的“阶段”,DP的状态表示中,第一维通常是节点编号(代表以该节点为根的子树)。
自底向上dfs,属于树的后序遍历
树形dp + 路径问题
树的最长路径
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
现在请你找到树中的一条最长路径。
换句话说,要找到一条路径,使得使得路径两端的点的距离最远。
注意:路径中可以只包含一个点。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示树的最长路径的长度。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
−105≤ci≤105
输入样例:
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
思路
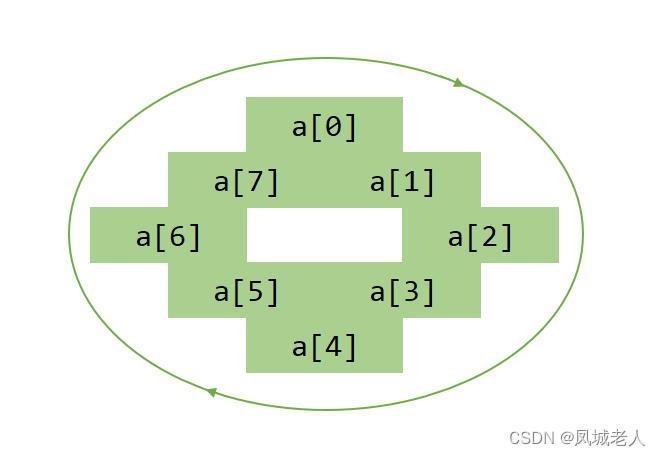
枚举路径的中间节点
我们先讨论一下,对于给定拓扑结构的树里的任意节点,经过他的路径有哪些: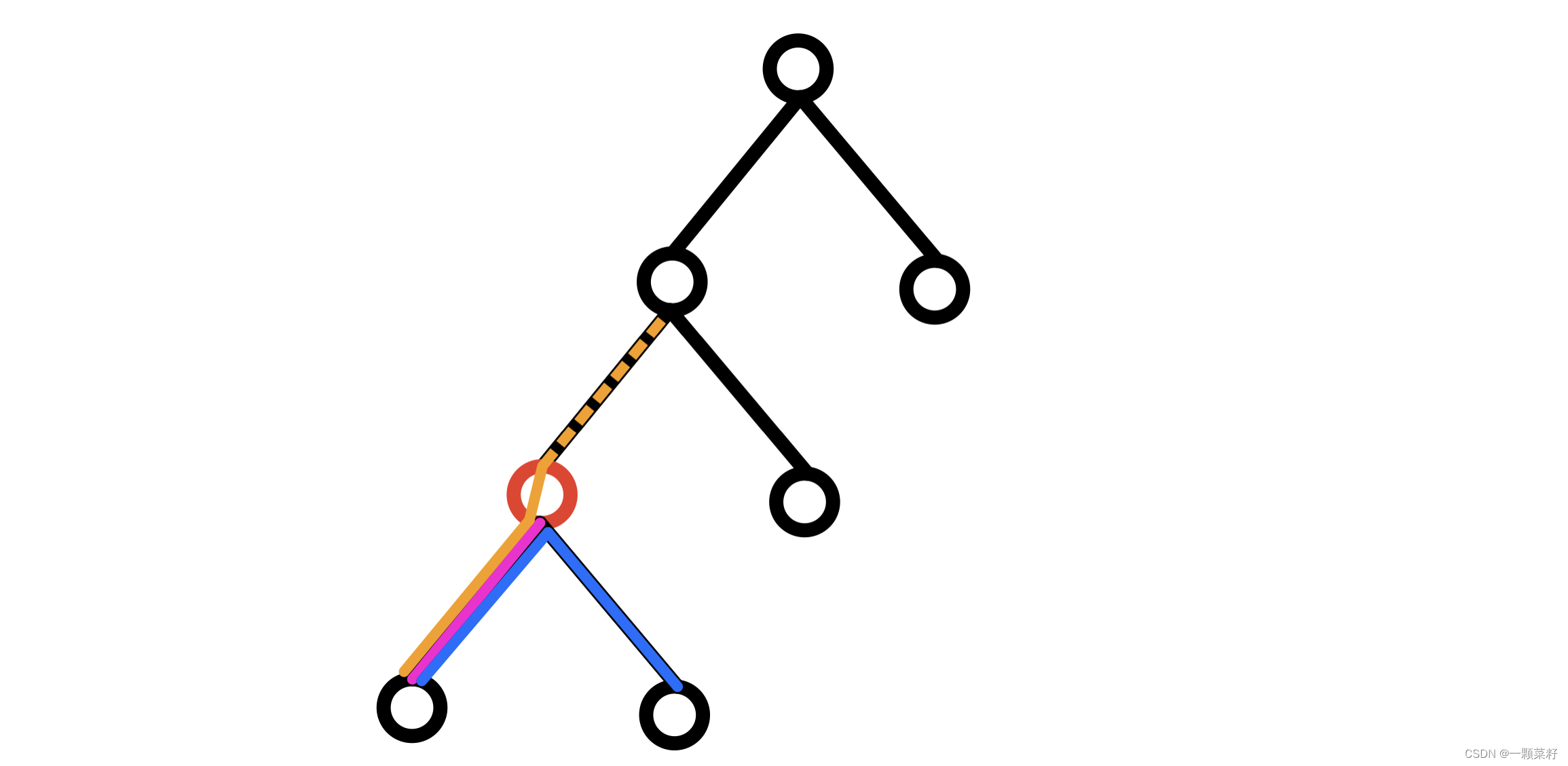
观察我标出的 红色节点,那么经过他的路径有:
以其 子树中的某个节点 作为 起点,以他作为 终点 的 粉色路径
以其 子树中的某个节点 作为 起点,以 子树中的某个节点 作为 终点 的 蓝色路径
以其 子树中的某个节点 作为 起点,以 非其子树的节点 作为 终点 的 橙色路径
对于第 1 种情况,我们可以直接递归处理其子树,找出到当前子树根节点最长的路径长度即可
对于第 2种情况,我们在处理第 1 种情况时,顺便找出 1类路径的 次长路径
把 最长 和 次长 拼在一起,就是我们要的第 2 种情况
而对于第 3 种情况,我们可以把它归类为其 祖先节点 的第 1,2种情况,让其 祖先节点去处理即可

代码
N, M = 10010, 10010 * 2
h = [-1] * N
e = [0] * M
w = [0] * M
ne = [-1] * M
idx = 0
d1, d2 = [0] * N, [0] * N
ans = 0
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u, father) :
global ans
i = h[u]
while i != -1 :
j = e[i]
if j != father
dfs(j, u)
#最长路径和次长路径的逻辑
if d1[u] <= d1[j] + w[i] :
d1[u], d2[u] = d1[j] + w[i], d1[u]
elif d2[u] < d1[j] + w[i] :
d2[u] = d1[j] + w[i]
i = ne[i]
ans = max(ans, d1[u] + d2[u]) #找到以u为中心的最长路径
n = int(input())
for i in range(n - 1) :
a, b, c = map(int, input().split())
add(a, b, c), add(b, a, c) #无向边
dfs(1, -1)#任意取一个点为根节点
print(ans)
树的中心
给定一棵树,树中包含 n 个结点(编号1~n)和 n−1 条无向边,每条边都有一个权值。
请你在树中找到一个点,使得该点到树中其他结点的最远距离最近。
输入格式
第一行包含整数 n。
接下来 n−1 行,每行包含三个整数 ai,bi,ci,表示点 ai 和 bi 之间存在一条权值为 ci 的边。
输出格式
输出一个整数,表示所求点到树中其他结点的最远距离。
数据范围
1≤n≤10000,
1≤ai,bi≤n,
1≤ci≤105
输入样例:
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2
换根DP
此类题目特点是,给定一个树形结构,需要以每个节点为根进行一系列统计。我们一般通过两次扫描来求解此类题目。
- 第一次扫描时,任取一个点为根,在“有根树”上执行一次树形DP,也就是在回溯时发生的、自底向上的状态转移。
- 第二次扫描时,从刚才选出的根出发,对整棵树执行一次深度优先遍历,在每次递归前进行自顶向下的推导,计算出“换根”后的解。
思路
在确定树的 拓扑结构 后单独求一个节点的 最远距离时,会在该树上去比较哪些路径呢?
- 从当前节点往下,直到子树中某个节点的最长路径
- 从当前节点往上走到其父节点,再从其父节点出发且不回到该节点的最长路径
- 第一次扫描,任取一个点为根,进行一次树形DP,处理出当前子树对于根的最大距离和次大距离
- 第二次扫描,从刚才选出的根出发,对整棵树执行一次深度优先遍历,求解出每个节点的父节点子树到当前节点的最大距离
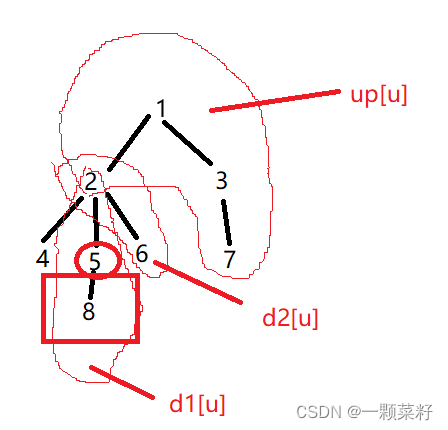
如图第二次扫描时,求解父节点的子树到5节点的距离时,需要考虑三种情况,1、父节点的子树到5节点的距离最长,即up[5],2、父节点子树的最长距离到节点5的距离最长,且与节点5最长距离不同路径,3、父节点子树的最长距离到节点5的距离最长,但与节点5最长距离同路径。
我们需要保存每个节点最长距离的子节点的编号
代码
N, M = 10010, 20010
h = [-1] * N
e = [0] * M
w = [0] * M
ne = [-1] * M
idx = 0
d1, d2, s, up= [0] * N, [0] * N, [0] * N, [0] * N
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
#记录每个节点的最长距离和次长距离,以及最长距离的子节点编号
def dfs_d(u, father) :
i = h[u]
while ~ i :
j = e[i]
if j != father :
dfs_d(j, u)
if d1[u] <= d1[j] + w[i] :
d1[u], d2[u], s[u] = d1[j] + w[i], d1[u], j
elif d2[u] < d1[j] + w[i] :
d2[u] = d1[j] + w[i]
i = ne[i]
# 处理每个节点途经父节点的最长距离
def dfs_u(u, father) :
i = h[u]
while ~ i :
j = e[i]
if j != father :
if j != s[u] : up[j] = max(up[u], d1[u]) + w[i]
else : up[j] = max(up[u], d2[u]) + w[i]
dfs_u(j, u)
i = ne[i]
n = int(input())
for i in range(n - 1) :
a, b, c = map(int, input().split())
add(a, b, c), add(b, a, c)
dfs_d(1, -1) # 任取一个点为根
dfs_u(1, -1) # 从刚才选出的根出发,对整棵树执行一次深度优先遍历
res = 10000010
for i in range(1, n + 1) :
res = min(res, max(d1[i], up[i]))
print(res)
数字转换
如果一个数 x 的约数之和 y(不包括他本身)比他本身小,那么 x 可以变成 y,y 也可以变成 x。
例如,4 可以变为 3,1 可以变为 7。
限定所有数字变换在不超过 n 的正整数范围内进行,求不断进行数字变换且不出现重复数字的最多变换步数。
输入格式
输入一个正整数 n。
输出格式
输出不断进行数字变换且不出现重复数字的最多变换步数。
数据范围
1≤n≤50000
输入样例:
7
输出样例:
3
样例解释
一种方案为:4→3→1→7。
思路
根据题意,单看一个数字 xx,那么他能转换到的数有:
- x的约数之和 x′(x′<x)
- 所有大于 x,且约数之和等于 x 的数 xi
那么我们就能绘出如下抽象图示了: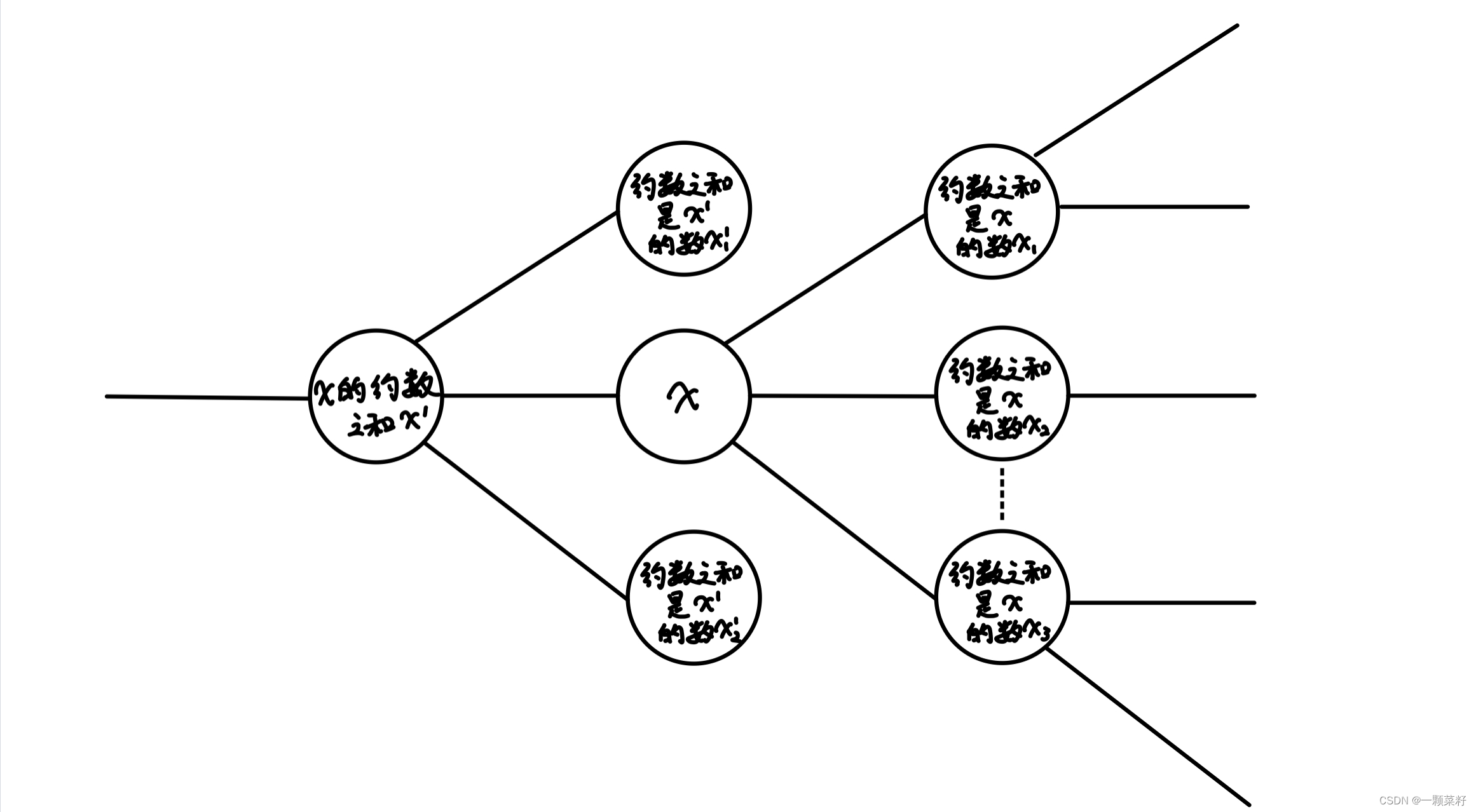
由于任意正整数 x,的 约数之和 是 唯一的,且本题要求只有约数之和 小于 自身才能转换
故对于所有的 x 来说,他向 小于 自己的数转换的边 至多 只有一条,那就是 x的 约数之和 x′(x′<x)
这样一个图论模型我们就很熟悉了,我们把每一个 数 看作一个 点,把上述这个 转换 看作该点的 入边
每一个 点,至多只有一条 入边,这就是 森林 呀
建好图后,本题就 等价于 找出一个森林中,直径最长 的树,并求出该树的直径
代码
N = 50010
h = [-1] * N
e = [0] * N
ne = [-1] * N
idx = 0
cumu = [0] * N
st = [False] * N
ans = 0
d1, d2 = [0] * N, [0] * N
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) : #求最长路径
global ans
i = h[u]
while ~ i :
j = e[i]
dfs(j)
if d1[u] <= d1[j] + 1 :
d1[u], d2[u] = d1[j] + 1, d1[u]
elif d2[u] < d1[j] + 1 :
d2[u] = d1[j] + 1
i = ne[i]
ans = max(ans, d1[u] + d2[u])
n = int(input())
# 筛法求约数
for i in range(1, n + 1) : #枚举所有两两相乘的情况,记录其中约数,除去本身
for j in range(2, n // i + 1) :
cumu[i * j] += i
for i in range(2, n + 1) : #1没有父节点
if i > cumu[i] :
add(cumu[i], i)
st[i] = True
for i in range(1, n + 1) :
if not st[i] : #枚举根节点
dfs(i)
print(ans)
树形dp + 有依赖的背包
二叉苹果树
有一棵二叉苹果树,如果树枝有分叉,一定是分两叉,即没有只有一个儿子的节点。
这棵树共 N 个节点,编号为 1 至 N,树根编号一定为 1。
我们用一根树枝两端连接的节点编号描述一根树枝的位置。
一棵苹果树的树枝太多了,需要剪枝。但是一些树枝上长有苹果,给定需要保留的树枝数量,求最多能留住多少苹果。
这里的保留是指最终与1号点连通。
输入格式
第一行包含两个整数 N 和 Q,分别表示树的节点数以及要保留的树枝数量。
接下来 N−1 行描述树枝信息,每行三个整数,前两个是它连接的节点的编号,第三个数是这根树枝上苹果数量。
输出格式
输出仅一行,表示最多能留住的苹果的数量。
数据范围
1≤Q<N≤100.
N≠1,
每根树枝上苹果不超过 30000 个。
输入样例:
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出样例:
21
思路
状态表示:
集合:设f[x, t]表示在以x为根的子树中选t个树枝能够保留的苹果数的集合
属性:集合中的苹果数的最大值
状态计算:
设x的子节点集合为Son(x),子节点个数
p
=
∣
S
o
n
(
x
)
∣
p = |Son(x)|
p=∣Son(x)∣。保留x这个节点后,对于x的每个节点
y
i
∈
S
o
n
(
x
)
y_i \in Son(x)
yi∈Son(x),我们可以在以
y
i
y_i
yi根节点的子树上选择保留若干节点(记数量为
c
i
c_i
ci),在满足
∑
i
=
1
p
c
i
=
t
\sum_{i=1}^pc_i = t
∑i=1pci=t
f
[
x
,
t
]
=
m
a
x
(
∑
i
=
1
p
f
[
y
i
,
c
i
]
)
+
w
[
x
,
y
i
]
,
(
∑
i
=
1
p
c
i
=
t
)
f[x, t] = max(\sum_{i=1}^pf[y_i, c_i]) + w[x, y _ i], \ ( \sum_{i = 1}^pc_i = t)
f[x,t]=max(i=1∑pf[yi,ci])+w[x,yi], (i=1∑pci=t)
该方程其实是一个分组背包模型。有
p
=
∣
S
o
n
(
x
)
∣
p = |Son(x)|
p=∣Son(x)∣组物品,每组物品都有t个,其中第i组的第j个物品的体积为j,价值为
f
[
y
i
,
j
]
f[y_i, j]
f[yi,j],背包的总体积为t。
代码
N, M = 110, 210
h = [-1] * N
e = [0] * M
ne = [0] * M
w = [0] * M
idx = 0
f = [[0] * N for _ in range(N)]
def add(a, b, c) :
global idx
e[idx] = b
w[idx] = c
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u, father) :
i = h[u]
while ~ i : #枚举物品组
ver = e[i]
if ver != father :
dfs(ver, u)
for j in range(m, -1, -1) : #枚举体积
for k in range(j) : #枚举物品组中的体积,枚举边数
f[u][j] = max(f[u][j], f[u][j - k - 1] + f[ver][k] + w[i])
i = ne[i]
n, m = map(int,input().split())
for i in range(n - 1) :
a, b, c = map(int, input().split())
add(a, b, c), add(b, a, c)
dfs(1, -1)
print(f[1][m])
树形dp + 状态机
没有上司的舞会
Ural 大学有 N 名职员,编号为 1∼N。
他们的关系就像一棵以校长为根的树,父节点就是子节点的直接上司。
每个职员有一个快乐指数,用整数 Hi 给出,其中 1≤i≤N。
现在要召开一场周年庆宴会,不过,没有职员愿意和直接上司一起参会。
在满足这个条件的前提下,主办方希望邀请一部分职员参会,使得所有参会职员的快乐指数总和最大,求这个最大值。
输入格式
第一行一个整数 N。
接下来 N 行,第 i 行表示 i 号职员的快乐指数 Hi。
接下来 N−1 行,每行输入一对整数 L,K,表示 K 是 L 的直接上司。
输出格式
输出最大的快乐指数。
数据范围
1≤N≤6000,
−128≤Hi≤127
输入样例:
7
1
1
1
1
1
1
1
1 3
2 3
6 4
7 4
4 5
3 5
输出样例:
5
思路
状态机模型
代码
import sys
N = 6010
sys.setrecursionlimit(N)
h = [-1] * N
e = [-1] * N
ne = [-1] * N
idx = 0
happy = [0] * N
has_fa = [False] * N
f = [[0, 0] for _ in range(N)]
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
f[u][1] = happy[u]
i = h[u]
while i != -1 :
j = e[i]
dfs(j)
f[u][0] += max(f[j][0], f[j][1])
f[u][1] += f[j][0]
i = ne[i]
n = int(input())
for i in range(1, n + 1) :
happy[i] = int(input())
for i in range(n - 1) :
a, b = map(int, input().split())
add(b, a)
has_fa[a] = True
root = 1
while has_fa[root] :
root += 1
dfs(root)
print(max(f[root][0], f[root][1]))
战略游戏
鲍勃喜欢玩电脑游戏,特别是战略游戏,但有时他找不到解决问题的方法,这让他很伤心。
现在他有以下问题。
他必须保护一座中世纪城市,这条城市的道路构成了一棵树。
每个节点上的士兵可以观察到所有和这个点相连的边。
他必须在节点上放置最少数量的士兵,以便他们可以观察到所有的边。
你能帮助他吗?
例如,下面的树:
只需要放置 1 名士兵(在节点 1 处),就可观察到所有的边。
输入格式
输入包含多组测试数据,每组测试数据用以描述一棵树。
对于每组测试数据,第一行包含整数 N,表示树的节点数目。
接下来 N 行,每行按如下方法描述一个节点。
节点编号:(子节点数目) 子节点 子节点 …
节点编号从 0 到 N−1,每个节点的子节点数量均不超过 10,每个边在输入数据中只出现一次。
输出格式
对于每组测试数据,输出一个占据一行的结果,表示最少需要的士兵数。
数据范围
0<N≤1500,
一个测试点所有 N 相加之和不超过 300650。
输入样例:
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
思路
状态机模型:
状态表示:
集合:f[x, 0]表示从以x为根的子树中,一部分节点安排士兵,并且x节点不安排士兵的士兵数的集合
f[x, 1]表示从以x为根的子树中,一部分节点安排士兵,并且x节点安排士兵的士兵数的集合
属性:士兵数的最小值
状态计算:
f
[
x
,
1
]
=
∑
s
∈
S
o
n
(
x
)
m
i
n
(
f
[
s
,
0
]
,
f
[
s
,
1
]
)
+
1
f
[
x
,
0
]
=
∑
s
∈
S
o
n
(
x
)
f
[
s
,
1
]
f[x, 1] = \sum_{s \in Son(x)} min(f[s, 0], f[s, 1]) + 1\\f[x, 0] = \sum_{s \in Son(x)}f[s, 1]
f[x,1]=s∈Son(x)∑min(f[s,0],f[s,1])+1f[x,0]=s∈Son(x)∑f[s,1]
代码
import sys
sys.setrecursionlimit(6000)
N = 1510
e = [0] * N
ne = [-1] * N
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
f[u][1] = 1
i = h[u]
while ~ i :
j = e[i]
dfs(j)
f[u][0] += f[j][1]
f[u][1] += min(f[j][1], f[j][0])
i = ne[i]
while True :
try :
n = int(input())
except : break
h = [-1] * N
st = [False] * N
idx = 0
f = [[0] * 2 for _ in range(N)]
for _ in range(n) :
cmd = input().split(':')
u = int(cmd[0])
for i in map(int, cmd[1].split(')')[1].split()) :
add(u, i)
st[i] = True
root = 0
for i in range(n) :
if not st[i] :
root = i
break
dfs(root)
print(min(f[root][0], f[root][1]))
皇宫看守
太平王世子事件后,陆小凤成了皇上特聘的御前一品侍卫。
皇宫各个宫殿的分布,呈一棵树的形状,宫殿可视为树中结点,两个宫殿之间如果存在道路直接相连,则该道路视为树中的一条边。
已知,在一个宫殿镇守的守卫不仅能够观察到本宫殿的状况,还能观察到与该宫殿直接存在道路相连的其他宫殿的状况。
大内保卫森严,三步一岗,五步一哨,每个宫殿都要有人全天候看守,在不同的宫殿安排看守所需的费用不同。
可是陆小凤手上的经费不足,无论如何也没法在每个宫殿都安置留守侍卫。
帮助陆小凤布置侍卫,在看守全部宫殿的前提下,使得花费的经费最少。
输入格式
输入中数据描述一棵树,描述如下:
第一行 n,表示树中结点的数目。
第二行至第 n+1 行,每行描述每个宫殿结点信息,依次为:该宫殿结点标号 i,在该宫殿安置侍卫所需的经费 k,该结点的子结点数 m,接下来 m 个数,分别是这个结点的 m 个子结点的标号 r1,r2,…,rm。
对于一个 n 个结点的树,结点标号在 1 到 n 之间,且标号不重复。
输出格式
输出一个整数,表示最少的经费。
数据范围
1≤n≤1500
输入样例:
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
样例解释:
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
思路
父节点 放置 哨兵,所有子节点都 可放可不放 哨兵
父节点 不放 哨兵,但是他至少有一个 子节点 放置哨兵,观察住了他
父节点 不放 哨兵,但 父节点 的 父节点 放置哨兵观察,则 子节点 可放可不放 哨兵
状态机模型
- 被父节点观察 ,不被自己观察(0)
- 被子节点观察,不被自己观察(1)
- 被自己来观察 (2)

代码
import sys
sys.setrecursionlimit(1510)
N = 1510
st = [False] * N
h = [-1] * N
e = [0] * N
ne = [-1] * N
w = [0] * N
idx = 0
f = [[0, 0, 0] for _ in range(N)]
def add(a, b) :
global idx
e[idx] = b
ne[idx] = h[a]
h[a] = idx
idx += 1
def dfs(u) :
f[u][2] = w[u]
i = h[u]
while ~ i :
j = e[i]
dfs(j)
#当前节点被父节点看管,并且不被自己看管,则子节点要么被自己看管要么被子节点的子节点看管
f[u][0] += min(f[j][1], f[j][2])
#当前节点被自己看管,则子节点可以自己看管也可以被父节点或子节点看管
f[u][2] += min(f[j][0], f[j][1], f[j][2])
i = ne[i]
i = h[u]
f[u][1] = int(1e9)
while ~ i :
j = e[i]
'''当前节点被子节点看管,且不被自己看管
枚举被哪个子节点看管,此时当前节点一定被自己看管
,其余子节点情况是可以被自己看管也可以被子节点的子节点看管,即
当前节点被父节点看管,并且不被自己看管,减去其中当前节点
自己看管也可以被子节点的子节点看管的最小值的情况
'''
f[u][1] = min(f[u][1], f[j][2] + f[u][0] - min(f[j][1], f[j][2]))
i = ne[i]
n = int(input())
for _ in range(n) :
cmd = list(map(int, input().split()))
ver = cmd[0]
w[ver], son = cmd[1], cmd[3 : ]
for i in son :
add(ver, i)
st[i] = True
root = 0
for i in range(1, n + 1) :
if not st[i] :
root = i
dfs(root)
print(min(f[root][1], f[root][2]))
总结
树形dp,好难\doge
////////////////////////////////////////////////////////////////////
// _ooOoo_ //
// o8888888o //
// 88" . "88 //
// (| ^_^ |) //
// O\ = /O //
// ____/`---'\____ //
// .' \\| |// `. //
// / \\||| : |||// \ //
// / _||||| -:- |||||- \ //
// | | \\\ - /// | | //
// | \_| ''\---/'' | | //
// \ .-\__ `-` ___/-. / //
// ___`. .' /--.--\ `. . ___ //
// ."" '< `.___\_<|>_/___.' >'"". //
// | | : `- \`.;`\ _ /`;.`/ - ` : | | //
// \ \ `-. \_ __\ /__ _/ .-` / / //
// ========`-.____`-.___\_____/___.-`____.-'======== //
// `=---=' //
// ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ //
// 佛祖保佑 永无BUG 永不修改 //
////////////////////////////////////////////////////////////////////