摘要:本文总体内容为介绍用最邻近方法(Nearest Neighbor Algorithm) 和最邻近插入法求解旅行商问题(Traveling Saleman Problem,TSP)。同时使用python实现算法,并调用networkx库实现可视化。此文为本人图论课下作业的成品,含金量:无。
关键词: TSP近似解; 最近邻方法;图论水作业
1. 前言
1.1 旅行商问题
旅行商问题,即TSP问题,又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。
用图论的话来说,旅行商问题是在加权完全无向图中,求经过每个结点恰好一次的(边)权和最小的哈密顿回路,又称之为最优哈密顿回路。[1]
若选定出发点,对n个城市进行排列,总共有(n-1)!条哈密顿回路,而一条哈密顿回路可以用相反两个方向来遍历,所以只需检查(n-1)!/2个哈密顿回路,从中找出权和最小的一个。而(n-1)!/2随n的增长而增长得极快,目前又没有一个有效算法来解决旅行商问题,所以解决旅行商问题的实际方法是使用其他方法来获取其近似解。
下用“最邻近方法”与“最邻近插入法”来获得旅行商问题的近似解。
1.2 最邻近方法
该算法的具体流程如下:给定源点作为线路的起点,寻找并加入距离上一次加入线路中顶点(城市)最近的顶点(城市),依次重复直到所有顶点(城市)已经加入线路,最后将源点加入到线路末尾即可。
该法本质是贪心策略(以距离上一次加入的顶点最近的点为策略)在线路中的具体实现,由于贪心算法在复杂问题中未必能得到最优解,因而该方法通常不能得到问题真正的最优路径,但胜在直观和速度较快。
1.3 最邻近插入法
最邻近方法由于所选取的哈密顿回路不同,所产生的近似解也不同,而“最邻近插入法”是对上述方法的改进。该方法的算法流程如下:
(1)假设图中有n个结点,任取图中一点Vi,作回路ViVi,置k=1;
(2)若k=n,则输出回路,否则,转为(3);
(3)在已有回路Ck=V1V2…VkV1之外的结点V-{V1V2…Vk}中,选取与回路Ck最近邻的点u;
(4)将u插入回路Ck的不同位置,可得k条不同回路,从中选取长度最小回路作为新回路。k=k+1, 转(2)。
2. 实验
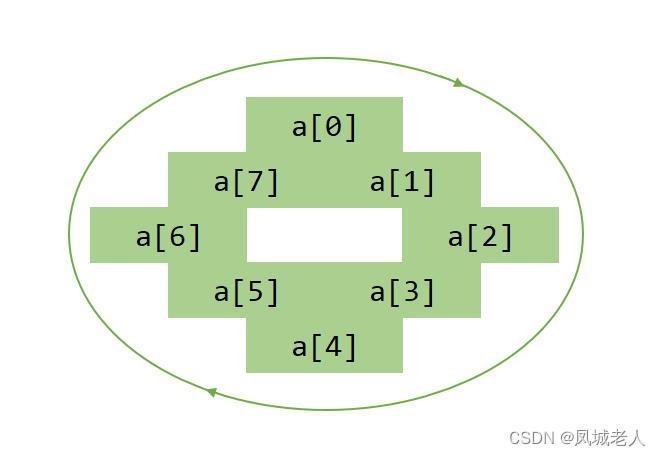
下面,我们使用python实现1.2,1.3中的算法,并举一例来计算求得旅行商问题的近似解。代码见附录。示例由代码随机产生,如图2.1所示。

图2.1 带权无向完全图示例
然后我们使用1.2中介绍的最邻近算法来生成TSP问题的近似解。如下图2.2所示,可以看到,所选取的初始出发点不同,所产生的哈密顿回路可能不同。而“最邻近插入法”是对最邻近算法的改进,从而产生一个比较好的结果,如下图2.3所示。可见,不管是任取哪个起点,最邻近插入法的寻找最短哈密顿回路的近似解效果比最邻近算法法好。

图2.2 最邻近算法求TSP问题近似解

图2.3 最邻近插入算法求TSP问题近似解
参考文献
[1] 张清华.图论及其应用[M].北京:清华大学出版社.2013.
附录:
1.源码链接
2. 挺有意思的一段话
那些知名度很高的好框架估计很多人都会提,答主再提也是重复劳动。而且题主试用之后,估计也确实会觉得它们中的部分或全部“嗯,不错,是挺好。”
然后选择其中一个一直用下去,从此过上了幸福的生活……
可喜可贺…
………
……
呃,不觉得少了点什么?
少吗?哪里少?
好吧,没什么…
……
…
平淡的生活何尝不是一种至高的幸福,
但是……如果有另一种机会,另一种选择,另一种人生可以经历……当我们老去,我们会不会为当初的选择而后悔?
或许另一种选择没有这么平静,没有这么顺利,可能充满挑战……
但,会不会,那才是生命中独特的一抹色彩?不可取代的重要体验?
因为那不是会让我说出“嗯,不错,是挺好”的东西,
而是……
“我X!!!这也行!!!!原来还可以这么搞啊!!!!!!!”
作者:Makoto Ruu 来源:知乎
链接
个人想法:有些别人提供给你的东西若达不到你想要的要求,那何不尝试着亲自动手打造并雕琢到心满意足。