【信息论与编码 沈连丰】第四章:离散信源的信源编码
- 第四章 离散信源的信源编码
- 4.1 信源编码的模型
- 4.2 信息传输速率和编码效率
- 4.3 单义可译定理
- 4.4 无失真信源编码定理
- 4.5 几种典型的信源编码方法
- 4.6 汉字编码方法及其讨论
- 4.7 图像的信源编码
- 4.8 误码对信源译码的影响
第四章 离散信源的信源编码
信源编码的含义:将信源产生的信息变换为数字序列的过程
信源编码的主要任务:将消息信号数字化和压缩其冗余度,提高编码效率
从编码结果使得信源消息的信息量有无损失的角度,可以分为无失真信源编码和限失真信源编码,其理论基础分别是香农第一定理和香农第三定理。
4.1 信源编码的模型
- ASCII码:

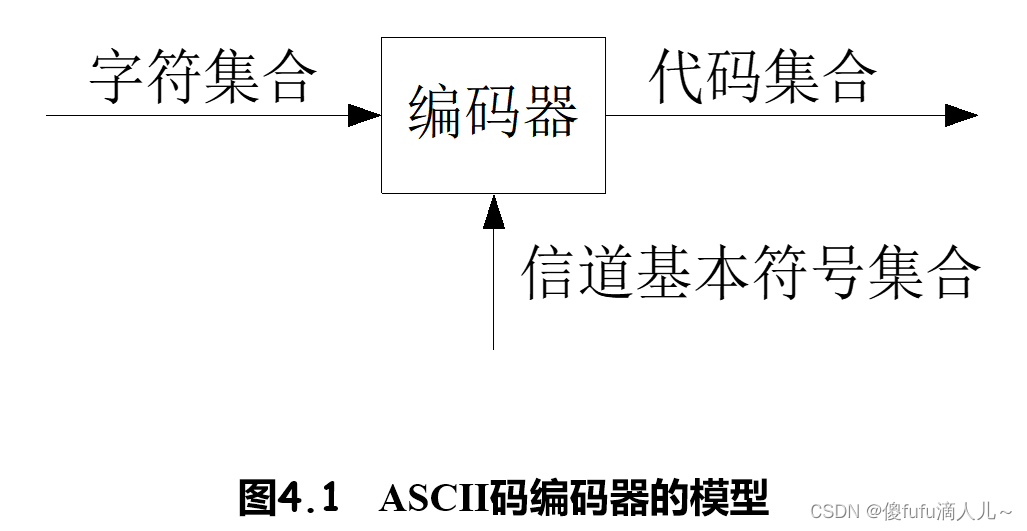

- 码字的平均长度最短和易于实现是编码时注重的两个方面,前者为了提高编码效率,后者为了性价比。
4.2 信息传输速率和编码效率
-
信息传输速率:

-
等长码的信息传输速率:

-
变长码的信息传输速率:



-
信道容量、编码效率:


-
信源最大熵与信道容量:

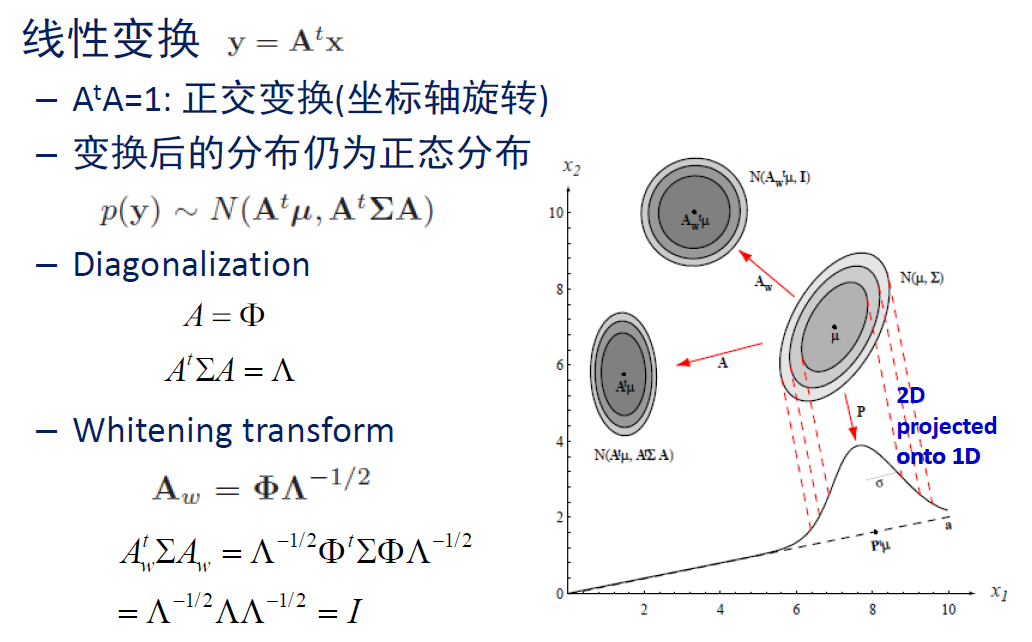
- 最佳编码:从编码效率公式可以看出,在给定信源情况下,若要提高信源编码的编码效率,方法之一就是使得编码后码字的平均长度尽可能小。通常称具有最短码字平均长度或编码效率趋近于1的信源编码为最佳信源编码。

4.3 单义可译定理
- 单义可译码:

-
即时码:译码时不需要考察后续码元,即时可译的码字。反之,如果需要考察后续码元的码字则称为非即时码。
-
即时可译码一定是单义可译码。反之不成立,即单义可译码不一定是即时码。如:
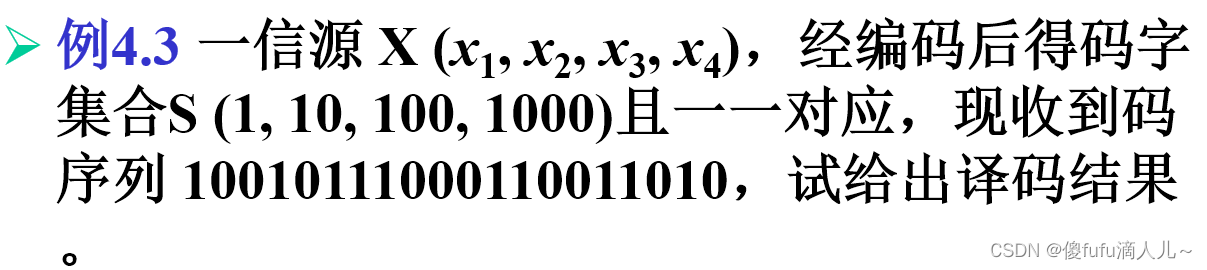
- Kraft不等式:给出了即时码存在的充要条件


-
Kraft不等式给出了即时码/单义可译码的要求,它只与码的结构有关,与信源消息的统计特性无关,它也没有给出是否为最佳编码的判断。
-
平均码长界定定理:






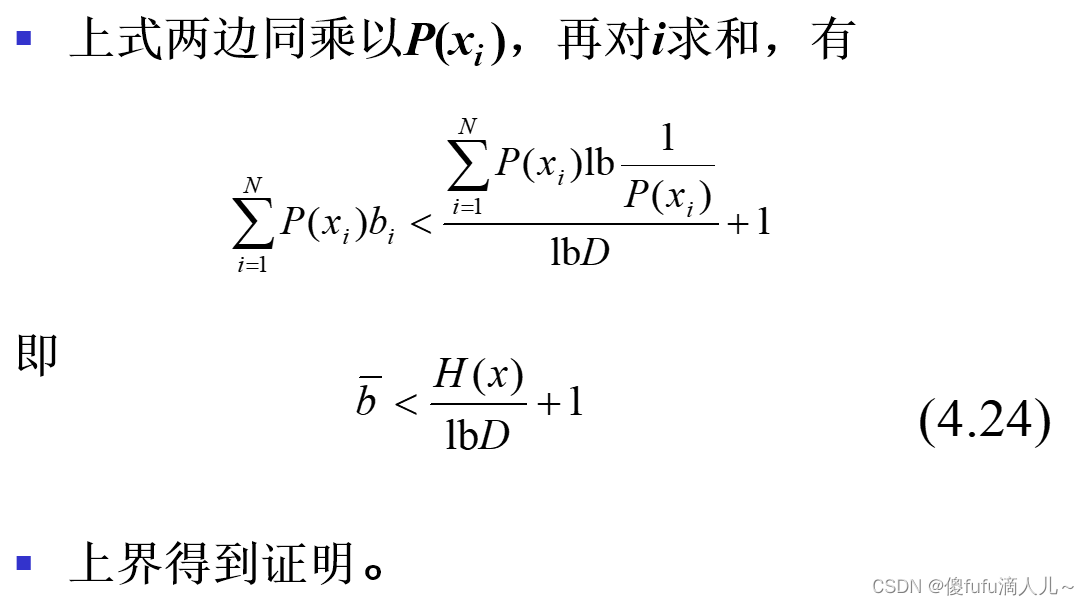
- 平均码长界定定理的物理意义:

4.4 无失真信源编码定理
- 二进制编码和无记忆信源条件下的香农第一定理:

- 香农第一定理:又称无失真信源编码定理或变长码信源编码定理



香农第一定理的意义是指:将原始信源符号转化为新的码元符号,使码元符号尽量服从等概分布,从而每个码元符号所携带的信息量达到最大,进而可以用尽量少的码元符号来传输信源信息。
- 香农第一定理仅仅是一个存在性定理。
4.5 几种典型的信源编码方法
-
香农编码:



例子:
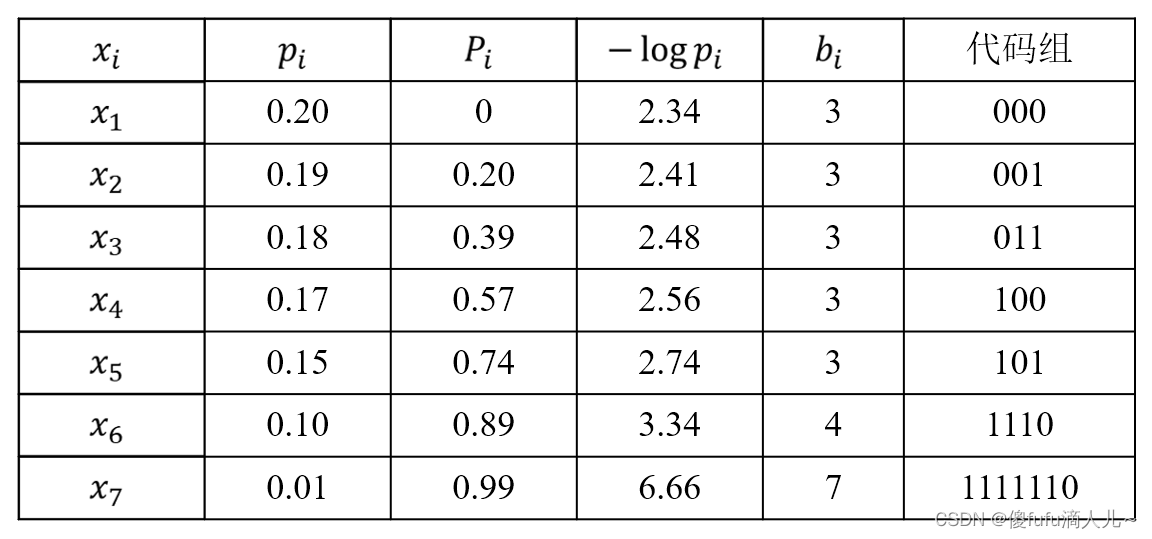
- 费诺编码:


例子:
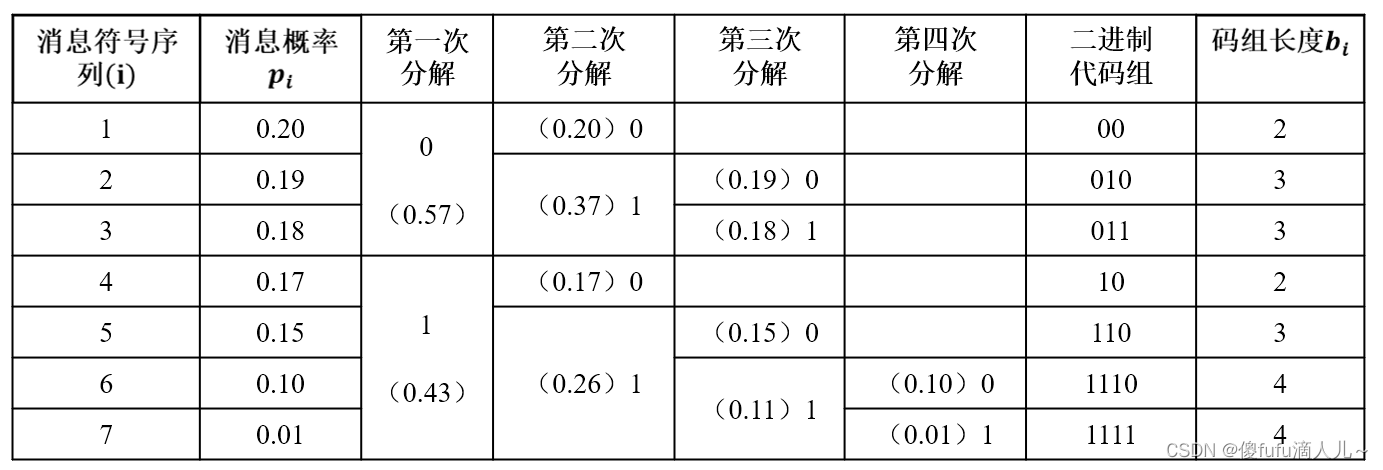
- 霍夫曼编码:



- Lempel-Ziv编码:





4.6 汉字编码方法及其讨论

4.7 图像的信源编码
-
压缩编码



-
算术编码

- 游程编码

- 轮廓编码

4.8 误码对信源译码的影响