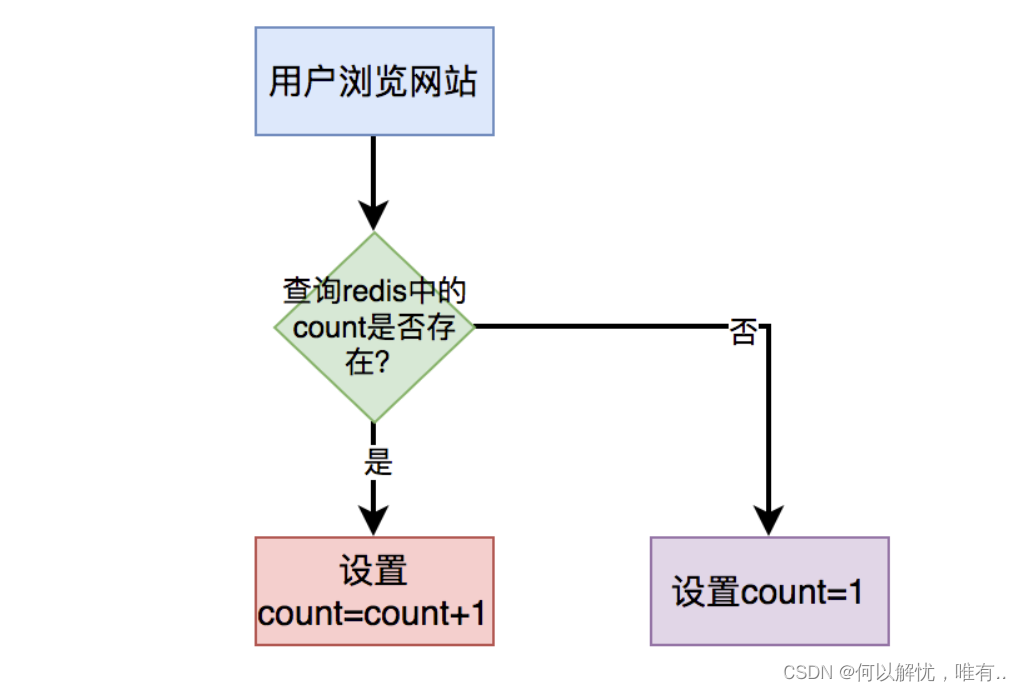
【题目一】设 ω max \omega_{\max } ωmax 为类别状态, 此时对所有的 i ( i = 1 , … , c ) i(i=1, \ldots, c) i(i=1,…,c), 有 P ( ω max ∣ x ) ≥ P\left(\omega_{\max } \mid \boldsymbol{x}\right) \geq P(ωmax∣x)≥ P ( ω i ∣ x ) P\left(\omega_i \mid \boldsymbol{x}\right) P(ωi∣x)
- 证明
P
(
ω
max
∣
x
)
≥
1
/
c
P\left(\omega_{\max } \mid \boldsymbol{x}\right) \geq 1 / c
P(ωmax∣x)≥1/c(最大值大于平均值)
P ( ω max ∣ x ) ≥ 1 c ∑ i = 1 c P ( ω i ∣ x ) = 1 c P\left(\omega_{\max } \mid \boldsymbol{x}\right) \geq \frac{1}{c} \sum_{i=1}^c P\left(\omega_i \mid \boldsymbol{x}\right)=\frac{1}{c} P(ωmax∣x)≥c1i=1∑cP(ωi∣x)=c1 - 证明对于最小错误率判定规则, 平均错误概率为
P ( error ) = 1 − ∫ P ( ω max ∣ x ) p ( x ) d x P(\text { error })=1-\int P\left(\omega_{\max } \mid \boldsymbol{x}\right) p(\boldsymbol{x}) d \boldsymbol{x} P( error )=1−∫P(ωmax∣x)p(x)dx
【解】当
ω
max
\omega_{\text {max }}
ωmax 不是样本的真实类别时, 决策出错, 因此错误率为(回忆一下期望公式)
P
(
error
)
=
E
x
(
1
−
P
(
ω
max
∣
x
)
)
=
1
−
∫
P
(
ω
max
∣
x
)
p
(
x
)
d
x
P(\text { error })=\mathbb{E}_x\left(1-P\left(\omega_{\max } \mid \boldsymbol{x}\right)\right)=1-\int P\left(\omega_{\max } \mid \boldsymbol{x}\right) p(\boldsymbol{x}) d \boldsymbol{x}
P( error )=Ex(1−P(ωmax∣x))=1−∫P(ωmax∣x)p(x)dx
- 利用这两个结论证明 P ( e r r o r ) ≤ ( c − 1 ) / c P( error ) \leq(c-1) / c P(error)≤(c−1)/c
【解】由 (1)(2) 的结论
P
(
error
)
=
1
−
∫
P
(
ω
max
∣
x
)
p
(
x
)
d
x
≤
1
−
∫
1
c
p
(
x
)
d
x
=
c
−
1
c
P(\text { error })=1-\int P\left(\omega_{\max } \mid \boldsymbol{x}\right) p(\boldsymbol{x}) d \boldsymbol{x} \leq 1-\int \frac{1}{c} p(\boldsymbol{x}) d \boldsymbol{x}=\frac{c-1}{c}
P( error )=1−∫P(ωmax∣x)p(x)dx≤1−∫c1p(x)dx=cc−1
- 描述一种情况, 在此情况下有 P ( e r r o r ) = ( c − 1 ) / c P( error )=(c-1) / c P(error)=(c−1)/c
【解】当对任意类别 i i i 都有 P ( ω i ∣ x ) = 1 / c P\left(\omega_i \mid \boldsymbol{x}\right)=1 / c P(ωi∣x)=1/c 时, P ( e r r o r ) = ( c − 1 ) / c P(error )=(c-1) / c P(error)=(c−1)/c
【题目二】对于一个 c c c 类分类问题, 假设各类先验概率为 P ( ω i ) , i = 1 , … , c P\left(\omega_i\right), i=1, \ldots, c P(ωi),i=1,…,c; 条件概率密度为 P ( x ∣ ω i ) , i = 1 , … , c , ( x P\left(\boldsymbol{x} \mid \omega_i\right), i=1, \ldots, c,(\boldsymbol{x} P(x∣ωi),i=1,…,c,(x 表示特征向量 ) ) ); 将第 j j j 类样本判别为第 i i i 类的损失为 λ i j \lambda_{i j} λij
- 请写出贝叶斯风险最小决策和最小错误率决策的决策规则
【解】最小风险决策:
argmin
i
R
(
α
i
∣
x
)
\underset{i}{\operatorname{argmin}} R\left(\alpha_i \mid \boldsymbol{x}\right)
iargminR(αi∣x)
其中,
R
(
α
i
∣
x
)
=
∑
j
=
1
c
λ
(
α
i
∣
ω
j
)
P
(
ω
j
∣
x
)
R\left(\alpha_i \mid \boldsymbol{x}\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid \boldsymbol{x}\right)
R(αi∣x)=∑j=1cλ(αi∣ωj)P(ωj∣x).
最小错误率决策: 此时风险为 0-1 loss, 即
λ
(
α
i
∣
ω
j
)
=
{
0
,
i
=
j
1
,
i
≠
j
\lambda\left(\alpha_i \mid \omega_j\right)=\left\{\begin{array}{l}0, i=j \\ 1, i \neq j\end{array}\right.
λ(αi∣ωj)={0,i=j1,i=j
R
(
α
i
∣
x
)
=
∑
j
=
1
c
λ
(
α
i
∣
ω
j
)
P
(
ω
j
∣
x
)
=
∑
j
≠
i
P
(
ω
j
∣
x
)
=
1
−
P
(
ω
i
∣
x
)
R\left(\alpha_i \mid \boldsymbol{x}\right)=\sum_{j=1}^c \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid \boldsymbol{x}\right)=\sum_{j\ne i}P\left(\omega_j \mid \boldsymbol{x}\right)=1-P\left(\omega_i \mid x\right)
R(αi∣x)=j=1∑cλ(αi∣ωj)P(ωj∣x)=j=i∑P(ωj∣x)=1−P(ωi∣x)
决策为
arg
max
i
P
(
ω
i
∣
x
)
\underset{i}{\arg \max } P\left(\omega_i \mid x\right)
iargmaxP(ωi∣x).
- 引入拒识 (表示为第
c
+
1
c+1
c+1 类), 假设决策损失为
λ ( α i ∣ ω j ) = { 0 , i = j i , j = 1 , … , c λ r , i = c + 1 λ s , otherwise \lambda\left(\alpha_i \mid \omega_j\right)= \begin{cases}0, & i=j \quad i, j=1, \ldots, c \\ \lambda_r, & i=c+1 \\ \lambda_s, & \text { otherwise }\end{cases} λ(αi∣ωj)=⎩ ⎨ ⎧0,λr,λs,i=ji,j=1,…,ci=c+1 otherwise
请写出最小风险决策的决策规则 (包括分类规则和拒识规则)
【解】注意这边按照定义,
c
+
1
c+1
c+1类判别为
i
i
i 类的风险也是
λ
s
\lambda_s
λs(注意理解这个拒识的定义,很绕,我用排除法,如果不属于第一种情况,又不属于第二种情况,那就是第三种情况)
R
(
α
i
∣
x
)
=
∑
j
=
1
c
+
1
λ
(
α
i
∣
ω
j
)
P
(
ω
j
∣
x
)
=
λ
s
[
1
−
P
(
ω
i
∣
x
)
]
,
i
=
1
,
⋯
,
c
R\left(\alpha_i \mid \boldsymbol{x}\right)=\sum_{j=1}^{c+1} \lambda\left(\alpha_i \mid \omega_j\right) P\left(\omega_j \mid \boldsymbol{x}\right)=\lambda_s\left[1-P\left(\omega_i \mid \boldsymbol{x}\right)\right], i=1, \cdots, c
R(αi∣x)=j=1∑c+1λ(αi∣ωj)P(ωj∣x)=λs[1−P(ωi∣x)],i=1,⋯,c
注意这边按照定义,
c
+
1
c+1
c+1类判别为
c
+
1
c+1
c+1类的风险也是
λ
r
\lambda_r
λr
R
(
α
c
+
1
∣
x
)
=
∑
j
=
1
c
+
1
λ
(
α
c
+
1
∣
ω
j
)
P
(
ω
j
∣
x
)
=
λ
r
R\left(\alpha_{c+1} \mid \boldsymbol{x}\right)=\sum_{j=1}^{c+1} \lambda\left(\alpha_{c+1}\mid \omega_j\right) P\left(\omega_j \mid \boldsymbol{x}\right)=\lambda_r
R(αc+1∣x)=j=1∑c+1λ(αc+1∣ωj)P(ωj∣x)=λr
由
R
i
(
x
)
R_i(x)
Ri(x) 的定义可计算得:
R
i
(
x
)
=
{
λ
s
[
1
−
P
(
ω
i
∣
x
)
]
,
i
=
1
,
⋯
,
c
λ
r
,
reject
R_i(x)=\left\{\begin{array}{c} \lambda_s\left[1-P\left(\omega_i \mid \boldsymbol{x}\right)\right], i=1, \cdots, c \\ \lambda_r, \text { reject } \end{array}\right.
Ri(x)={λs[1−P(ωi∣x)],i=1,⋯,cλr, reject
因此, 带拒识的最小风险决策为:
arg
min
i
R
i
(
x
)
=
{
arg
max
i
P
(
ω
i
∣
x
)
,
if
max
P
(
ω
i
∣
x
)
>
1
−
λ
r
/
λ
s
reject, otherwise
\underset{i}{\arg \min } R_i(x)=\left\{\begin{array}{c} \underset{i}{\arg \max } P\left(\omega_i \mid \boldsymbol{x}\right), \text { if } \max P\left(\omega_i \mid \boldsymbol{x}\right)>1-\lambda_r / \lambda_s \\ \text { reject, otherwise } \end{array}\right.
iargminRi(x)={iargmaxP(ωi∣x), if maxP(ωi∣x)>1−λr/λs reject, otherwise
【题目三】考虑三维正态分布
p
(
x
∣
ω
)
∼
N
(
μ
,
Σ
)
p(\boldsymbol{x} \mid \omega) \sim N(\boldsymbol{\mu}, \Sigma)
p(x∣ω)∼N(μ,Σ), 其中
μ
=
(
1
2
2
)
,
Σ
=
(
1
0
0
0
5
2
0
2
5
)
\boldsymbol{\mu}=\left(\begin{array}{l} 1 \\ 2 \\ 2 \end{array}\right), \Sigma=\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 5 & 2 \\ 0 & 2 & 5 \end{array}\right)
μ=
122
,Σ=
100052025
- 构造白化变换 A ω = Φ Λ − 1 / 2 \mathrm{A}_\omega=\Phi \Lambda^{-1 / 2} Aω=ΦΛ−1/2, 计算分别表示本征向量和本征值的矩阵 Φ \Phi Φ 和 Λ \Lambda Λ; 接下来, 将此分布转换为以原点为中心、协方差矩阵为单位阵的分布, 即 p ( x ∣ ω ) ∼ N ( 0 , I ) p(\boldsymbol{x} \mid \omega) \sim N(\mathbf{0}, \mathrm{I}) p(x∣ω)∼N(0,I)
【解】计算可知协方差矩阵
Σ
\Sigma
Σ 的本征值为:
λ
1
=
1
,
λ
2
=
3
,
λ
3
=
7
\lambda_1=1, \lambda_2=3, \lambda_3=7
λ1=1,λ2=3,λ3=7, 其对应的本征向量分别为:
v
1
=
(
0
,
1
,
−
1
)
T
/
2
,
v
2
=
(
0
,
1
,
1
)
T
/
2
,
v
3
=
v_1=(0,1,-1)^T / \sqrt{2}, v_2=(0,1,1)^T / \sqrt{2}, v_3=
v1=(0,1,−1)T/2,v2=(0,1,1)T/2,v3=
(
1
,
0
,
0
)
T
,
Φ
(1,0,0)^T, \Phi
(1,0,0)T,Φ 和
Λ
\Lambda
Λ 和
A
ω
A_\omega
Aω 为:
Φ
=
(
1
0
0
0
1
/
2
1
/
2
0
−
1
/
2
1
/
2
)
,
Λ
=
diag
(
1
,
3
,
7
)
A
ω
=
Φ
Λ
−
1
/
2
=
(
1
0
0
0
1
/
6
1
/
14
0
−
1
/
6
1
/
14
)
\begin{gathered} \Phi=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 / \sqrt{2} & 1 / \sqrt{2} \\ 0 & -1 / \sqrt{2} & 1 / \sqrt{2} \end{array}\right), \quad \Lambda=\operatorname{diag}(1,3,7) \\ \mathrm{A}_\omega=\Phi \Lambda^{-1 / 2}=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 / \sqrt{6} & 1 / \sqrt{14} \\ 0 & -1 / \sqrt{6} & 1 / \sqrt{14} \end{array}\right) \end{gathered}
Φ=
10001/2−1/201/21/2
,Λ=diag(1,3,7)Aω=ΦΛ−1/2=
10001/6−1/601/141/14
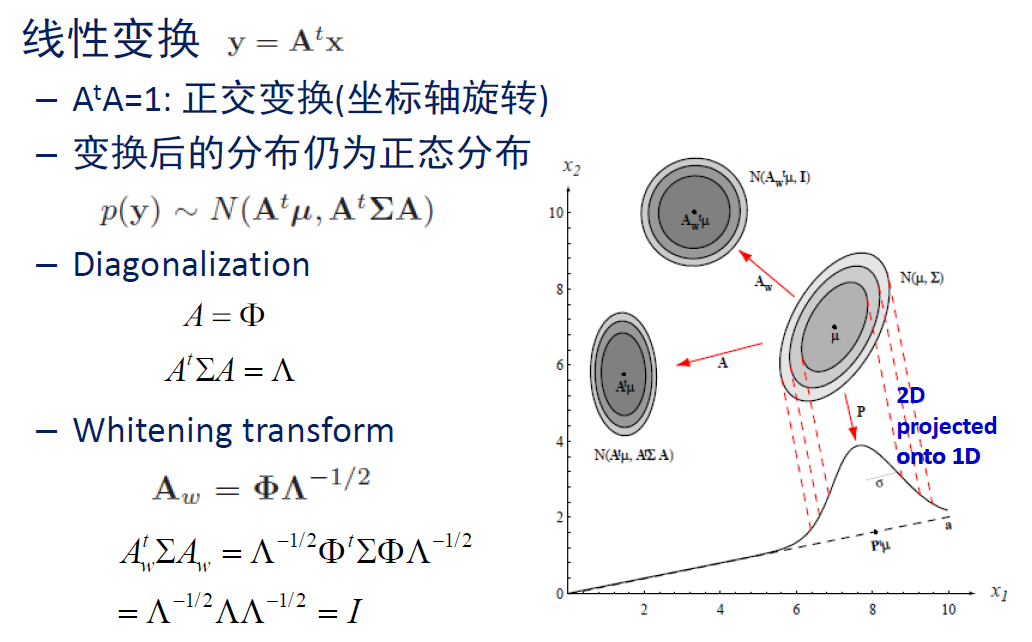
通过变换 y = A ω T ( x − μ ) \boldsymbol{y}=\mathrm{A}_\omega{ }^T(\boldsymbol{x}-\boldsymbol{\mu}) y=AωT(x−μ) 可将原分布变换到 N ( 0 , I ) N(\mathbf{0}, \mathrm{I}) N(0,I) (单纯的白化变换只能把协方差矩阵变为单位矩阵,这边要求均值为 0 0 0 ,所以还得平移一下)
- 将 (1) 中的白化变换应用于点 x 0 = ( 0.5 , 0 , 1 ) t \boldsymbol{x}_0=(0.5,0,1)^t x0=(0.5,0,1)t, 求其经过白化变换后的点 x ω x_\omega xω
【解】 x ω = A ω T ( x − μ ) = ( − 0.5 , − 1 / 6 , − 3 / 14 ) T \boldsymbol{x}_\omega=\mathrm{A}_\omega^T(\boldsymbol{x}-\boldsymbol{\mu})=(-0.5,-1 / \sqrt{6},-3 / \sqrt{14})^T xω=AωT(x−μ)=(−0.5,−1/6,−3/14)T
- 通过详细计算, 证明原分布中从 x 0 \boldsymbol{x}_0 x0 到均值 μ \boldsymbol{\mu} μ 的 Mahalanobis 距离与变换后的分布中从 x ω \boldsymbol{x}_\omega xω 到 0 \mathbf{0} 0 的 Mahalanobis 距离相等。
【解】 x 0 x_0 x0 到 μ \mu μ 的马氏距离为: 89 84 , x ω \sqrt{\frac{89}{84}}, x_\omega 8489,xω 到 0 的马氏距离为: 89 84 \sqrt{\frac{89}{84}} 8489, 两者相等
- 概率密度在一个一般的线性变换下是否保持不变? 换句话说, 对于某线性变换 T T T, 是否有 p ( x 0 ∣ N ( μ , Σ ) ) = p ( T t x 0 ∣ N ( T t μ , T t Σ T ) ) p\left(\boldsymbol{x}_0 \mid N(\boldsymbol{\mu}, \Sigma)\right)=p\left(T^t \boldsymbol{x}_0 \mid N\left(T^t \boldsymbol{\mu}, T^t \Sigma T\right)\right) p(x0∣N(μ,Σ))=p(Ttx0∣N(Ttμ,TtΣT)) ? 解释原因
【解】
p
(
T
t
x
0
∣
N
(
T
t
μ
,
T
t
Σ
T
)
)
=
1
(
2
π
)
d
/
2
∣
T
t
Σ
T
∣
1
/
2
exp
(
−
1
2
(
T
t
x
−
T
t
μ
)
t
(
T
t
Σ
T
)
−
1
(
T
t
x
−
T
t
μ
)
)
=
1
(
2
π
)
d
/
2
∣
T
t
Σ
T
∣
1
/
2
exp
(
−
1
2
(
x
−
μ
)
t
T
T
−
1
Σ
−
1
T
−
t
T
t
(
x
−
μ
)
)
=
1
(
2
π
)
d
/
2
∣
Σ
∣
1
/
2
exp
(
−
1
2
(
x
−
μ
)
t
Σ
−
1
(
x
−
μ
)
)
\begin{aligned} p\left(T^t \boldsymbol{x}_0 \mid N\left(T^t \boldsymbol{\mu}, T^t \Sigma T\right)\right) & =\frac{1}{(2 \pi)^{d / 2}\left|T^t \Sigma T\right|^{1 / 2}} \exp \left(-\frac{1}{2}\left(T^t x-T^t \mu\right)^t\left(T^t \Sigma T\right)^{-1}\left(T^t x-T^t \mu\right)\right) \\ & =\frac{1}{(2 \pi)^{d / 2}\left|T^t \Sigma T\right|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^t T T^{-1} \Sigma^{-1} T^{-t} T^t(x-\mu)\right) \\ & =\frac{1}{(2 \pi)^{d / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^t \Sigma^{-1}(x-\mu)\right) \end{aligned}
p(Ttx0∣N(Ttμ,TtΣT))=(2π)d/2∣TtΣT∣1/21exp(−21(Ttx−Ttμ)t(TtΣT)−1(Ttx−Ttμ))=(2π)d/2∣TtΣT∣1/21exp(−21(x−μ)tTT−1Σ−1T−tTt(x−μ))=(2π)d/2∣Σ∣1/21exp(−21(x−μ)tΣ−1(x−μ))
【题目四】对一个 c c c 类分类问题, 特征向量 x ∈ R d \boldsymbol{x} \in \mathcal{R}^d x∈Rd, 假设各类先验概率相等, 每一类条件概率密度为高斯分布
- 请写出类条件概率密度函数的数学形式
【解】类条件概率密度服从
d
d
d 维高斯分布, 故类条件概率密度函数的数学形式为:
p
(
x
∣
ω
i
)
=
1
(
2
π
)
d
/
2
∣
Σ
i
∣
1
/
2
exp
[
−
1
2
(
x
−
μ
i
)
T
Σ
i
−
1
(
x
−
μ
i
)
]
p\left(\boldsymbol{x} \mid \omega_i\right)=\frac{1}{(2 \pi)^{d / 2}\left|\Sigma_i\right|^{1 / 2}} \exp \left[-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^T \Sigma_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)\right]
p(x∣ωi)=(2π)d/2∣Σi∣1/21exp[−21(x−μi)TΣi−1(x−μi)]
- 请写出在下面两种情况下的最小错误率决策判别函数:(a) 类协方差矩阵不等; (b) 所有类协方差矩阵相等.
【解】判别函数计算公式为:
g
i
(
x
)
=
ln
p
(
x
∣
ω
i
)
+
ln
P
(
ω
i
)
g_i(\boldsymbol{x})=\ln p\left(\boldsymbol{x} \mid \omega_i\right)+\ln P\left(\omega_i\right)
gi(x)=lnp(x∣ωi)+lnP(ωi)
类协方差矩阵不等时:可以进一步写为:
g
i
(
x
)
=
−
1
2
(
x
−
μ
i
)
T
Σ
i
−
1
(
x
−
μ
i
)
−
d
2
ln
2
π
−
1
2
ln
∣
Σ
i
∣
+
ln
P
(
ω
i
)
g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^T \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|+\ln P\left(\omega_i\right)
gi(x)=−21(x−μi)TΣi−1(x−μi)−2dln2π−21ln∣Σi∣+lnP(ωi)
不考虑与类别
i
i
i 无关的项, 且由于各类先验概率相等, 进一步有:
g
i
(
x
)
=
−
1
2
(
x
−
μ
i
)
T
Σ
i
−
1
(
x
−
μ
i
)
−
1
2
ln
∣
Σ
i
∣
g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^T \boldsymbol{\Sigma}_i^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{1}{2} \ln \left|\boldsymbol{\Sigma}_i\right|
gi(x)=−21(x−μi)TΣi−1(x−μi)−21ln∣Σi∣
所有类协方差矩阵相等时: 可以进一步写为:
g
i
(
x
)
=
−
1
2
(
x
−
μ
i
)
T
Σ
−
1
(
x
−
μ
i
)
−
d
2
ln
2
π
−
1
2
ln
∣
Σ
∣
+
ln
P
(
ω
i
)
g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^T \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)-\frac{d}{2} \ln 2 \pi-\frac{1}{2} \ln |\boldsymbol{\Sigma}|+\ln P\left(\omega_i\right)
gi(x)=−21(x−μi)TΣ−1(x−μi)−2dln2π−21ln∣Σ∣+lnP(ωi)
不考虑与类别
i
i
i 无关的项, 且由于各类先验概率相等, 进一步有:
g
i
(
x
)
=
−
1
2
(
x
−
μ
i
)
T
Σ
−
1
(
x
−
μ
i
)
g_i(\boldsymbol{x})=-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)^T \boldsymbol{\Sigma}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_i\right)
gi(x)=−21(x−μi)TΣ−1(x−μi)
- 在基于高斯概率密度的二次判别函数中, 当协方差矩阵为奇异时, 判别函数变得不可计算。请说出两种克服协方差奇异的方法。
【解】a. 降维, 减少特征向量的维度, 使得较低维度的协方差矩阵可逆; b. 矩阵对角化之后在特征值为 0 的位置加上小的常数; c. 求伪逆矩阵。 Σ † = ( Σ T Σ ) − 1 Σ T \boldsymbol{\Sigma}^{\dagger}=\left(\boldsymbol{\Sigma}^T \boldsymbol{\Sigma}\right)^{-1} \boldsymbol{\Sigma}^T Σ†=(ΣTΣ)−1ΣT