一、判断题
1.若一个栈的输入序列为{1, 2, 3, 4, 5},则不可能得到{3, 4, 1, 2, 5}这样的出栈序列。(T)
3比4先进,所以3比4后出,所以不可能得到
2. 在二叉排序树中,每个结点的关键字都比左孩子关键字大,比右孩子关键字小。(T)
二叉排序树的定义是:在二叉树的左子树中,所有的结点的关键字都比根结点的关键字小;在二叉树的右子树中,所有的结点的关键字都比根结点的关键字大。
3. 在任何情况下,时间复杂度为O(n2) 的算法比时间复杂度为O(n*logn)的算法所花费的时间都长。(F)
数据量小的情况下,两者耗费的时间差不多
4. 在含有n个结点的树中,边数只能是n-1条。(T)
边数+1=结点数 所以边数=n-1
例如,1个点没有边,两个点一条边,三个点两条边
5. Prim 算法是通过每步添加一条边及其相连的顶点到一棵树,从而逐步生成最小生成树。(T)
最小生成树:在一个连通图的所有生成树中,各边代价之和最小的那棵生成树称为该连通图的最小代价生成树,简称最小生成树。
普里姆算法:在所有的u属于U,v属于V-U的边中,选一条代价最小的边并入集合(从一个顶点到另一个顶点不断延伸,dfs)
克鲁斯卡尔算法:1.将n个顶点看成n个集合 2按权值由小到大的顺序选择边,所选边应满足两个顶点不在同一个顶点的集合内,将该边放到生成树边的集合中,同时将该边的两个顶点所在的顶点集合合并 3.不断重复2,直到所有的顶点都在同一个顶点集合内(在同一个点向外扩散,bfs)
二、单选题
1.假设以行序为主序存储二维数组A=array[1..40,1..20],设每个数据元素占2个存储单元,基地址LOC[1,1]为2000,则LOC[11,14]的存储位置为(C ).
A.2468
B.2466
C.2426
D.2428
行序:2000+(10*20+13)*2=2426
2.完全二叉树顺序存储,结点X的编号为42,则其右孩子结点的编号是( D)
A.84
B.41
C.43
D.85
其右孩子的结点的编号为:n*2+1=42*2+1=85
3. 一棵二叉树,度为2结点数为69,度为1结点数为82,则叶子结点数为( A).
A.70
B.81
C.83
D.68
叶子结点=度为2的节点+1
4.有21个叶子的哈夫曼树的结点总数为 (B ).
A.440
B.41
C.42
D.43
叶子结点:21 度为2的节点为:20
21+20=41
5.具有17个结点的二叉树使用二叉链表进行存储,其中空指针的数目是( D).
A.16
B.34
C.136
D.18
若一个二叉树含有n个结点,则其二叉链表必含有2n个指针域,其中必有n+1个空链域,非空链域为n-1;
6. 已知序列4,13,21,22,40,42,54,71,87,103,104,则用折半查找法查找54需要进行( C)次比较.
A.4
B.2
C.3
D.1
log2(11)=3
7. 具有22个顶点,271条边的有向图,所有顶点度的和为( A).
A.542
B.271
C.44
D.231
所有顶点的度之和=边的总数*2
即:271*2=542
8. 具有46个顶点的无向图至少有多少条边才能形成连通图 ( B).
A.1035
B.45
C.46
D.47
三个顶点至少两条边,即n个顶点至少n-1条边
9. 完全二叉树的第8层有11个节点,该完全二叉树总计有多少个节点( B).
A 267
B.138
C.266
D.139
1+2+4+8+16+32+64+11=138
第七层有2^6个节点=64
10. 在一个单链表中,已知b结点,若在b后插入a结点,则须执行(A ).
A.a->next=b->next; b->next=a;
B.b->next=a; a->next=b;
C.b->next=a->next; a->next=b;
D.a->next=b; b->next=a->next
三、填空题
1.关于顺序查找算法
在下面的线性表中,
( 15, 24, 32, 47, 50, 58, 62, 79, 83, 96 )
若采用顺序查找算法,则最大查找长度为 10
n=10
顺序查找的平均查找长度,假设列表的长度为n,则平均查找长度为:(1/2)*(n+1)
顺序查找的最大查找长度:10(找到列表的末尾)
2. 对如下图所示的AOE网络,计算各事件(顶点)的最早发生时间和最晚发生时间,并填入结果表格。(请填写阿拉伯数字,数字前后不要有空格)
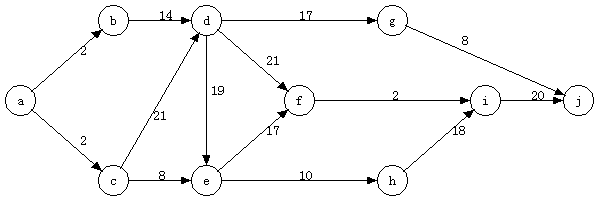
| a | b | c | d | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| ve | 0 | 2 | 2 | 23 | 42 | 59 | 40 | 52 | 70 | 90 |
| vl | 0 | 9 | 2 | 23 | 42 | 68 | 82 | 52 | 70 | 90 |
vl倒着看
g:j-g 90-8=82
i: j-i 90-20=70
f: i-f 70-2=68
e: f-e 68-17=51
h-e 52-10=42
取两者之间最小的
d:g-d 82-17=65;f-d 59-21=38;e-d 42-19=23
b:d-b 23-14=9
3. 顺序表 - 地址计算
假设顺序表第 1 个元素的内存地址是 100,每个元素占用 2 字节内存空间,则第 5 个元素的内存地址是 108
100+(5-1)*2=108
4. 基本术语
算法是对特定问题求解步骤的一种描述,它是指令的有限序列,其中每一条指令表示一个或多个操作。
5.若使用Prim算法从顶点W开始获取下图的最小生成树, 我们选择加入生成树的第二条边的权值是: 3
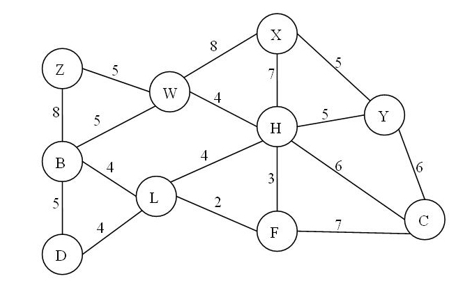
WH-HF
6. 一棵二叉树的前序遍历序列是ABDFECGHK,中序遍历序列是DBEFAGHCK,则它的后序遍历序列是 DEFBHGKCA

7. 普里姆算法
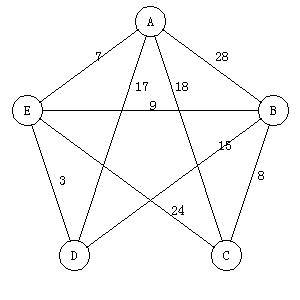
请写出用普里姆算法从顶点A出发生成最小生成树每一步加入的边
1.AE
2.ED
3.EB
4.BC