---

本系列文章介绍强化学习基础知识与经典算法原理，大部分内容来自西湖大学赵世钰老师的强化学习的数学原理课程（参考资料1），并参考了部分参考资料2、3的内容进行补充。

系列博文索引：（更新中）

• 强化学习的数学原理学习笔记 - RL基础知识
• 强化学习的数学原理学习笔记 - 基于模型（Model-based）
• 强化学习的数学原理学习笔记 - 蒙特卡洛方法（Monte Carlo）
• 强化学习的数学原理学习笔记 - 时序差分学习（Temporal Difference）

参考资料：

1. 【强化学习的数学原理】课程：从零开始到透彻理解（完结）（主要）
2. Sutton & Barto Book: Reinforcement Learning: An Introduction
3. 机器学习笔记

*注：【】内文字为个人想法，不一定准确

概览：RL方法分类

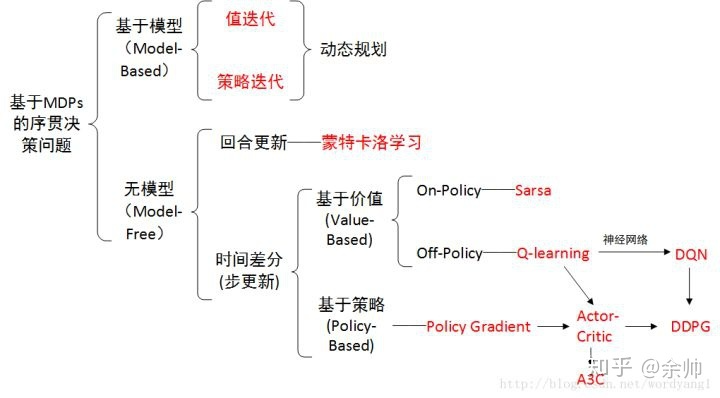
*图源：https://zhuanlan.zhihu.com/p/36494307

蒙特卡洛方法（Monte Carlo，MC）

求解RL问题，要么需要模型，要么需要数据。之前介绍了基于模型（model-based）的方法。然而在实际场景中，环境的模型（如状态转移函数）往往是未知的，这就需要用无模型（model-free）方法解决问题。

无模型的方法可以分为两大类：蒙特卡洛方法（Monte Carlo，MC）和时序差分学习（Temporal Difference，TD）。本文介绍蒙特卡洛方法。

蒙特卡洛思想：通过大数据量的样本采样来进行估计【本质上是大数定律的应用（基于独立同分布采样）】，将策略迭代中依赖于model的部分替换为model-free。

MC的核心idea：并非直接求解$q_{\pi }(s,a)$的准确值，而是基于数据（sample / experience）来估计$q_{\pi }(s,a)$的值。MC直接通过动作值的定义进行均值估计，即：
$$q_{\pi }(s,a)={\mathbb{E}}_{\pi }[G_t|S_t=s,A_t=a]\approx \frac{1}{N}\sum _{i=1}^N{g}^{(i)}(s,a)$$
其中$g^{(i)}(s,a)$表示对于$G_t$的第$i$个采样。

MC Basic

算法步骤：在第$k$次迭代中，给定策略${\pi }_k$（随机初始策略：${\pi }_0$）

• 策略评估：对每个状态-动作对$(s,a)$，运行无穷（或足够多）次episode，估算$q_{{\pi }_k}(s,a)$
• 策略提升：基于估算的$q_{{\pi }_k}(s,a)$，求解迭代策略${\pi }_{k+1}(s)={\mathrm{argmax}}_{\pi }{\sum }_a\pi (a|s)q_{{\pi }_k}(s,a)$

MC Basic与策略迭代的区别：在第$k$次迭代中

• 策略迭代使用迭代方法求出状态值$v_{{\pi }_k}$，并基于状态值求出动作值$q_{{\pi }_k}(s,a)$
• MC Basic直接基于采样/经验均值估计$q_{{\pi }_k}(s,a)$（不需要估计状态值）

*MC Basic只是用来说明MC的核心idea，并不会在实际中应用，因为其非常低效。

MC Exploring Starts

思想：提升MC Basic的效率

• 利用数据：对于一个轨迹，从后往前利用$(s,a)$状态-动作对采样做估计
  • 例如：对于轨迹$s_1\stackrel{a_2}{\to }{s}_2\stackrel{a_4}{\to }{s}_1\stackrel{a_2}{\to }{s}_2\stackrel{a_3}{\to }{s}_5\stackrel{a_1}{\to }\cdots$，从后往前采样，即先估计$q_{\pi }(s_5,a_1)$，再估计$q_{\pi }(s_2,a_3)=R_{t+4}+\gamma q_{\pi }(s_5,a_1)$，进而估计$q_{\pi }(s_1,a_2)=R_{t+3}+\gamma q_{\pi }(s_2,a_3)$，以此类推
• 更新策略：不必等待所有episode的数据收集完毕，直接基于单个episode进行估计，类似于截断策略迭代（单次估计不准确，但快）
  • 这是通用策略迭代（Generalized Policy Iteration，GPI）的思想

MC Exploring Starts

• Exploring：探索每个$(s,a)$状态-动作对
• Starts：从每个状态-动作对开始一个episode
  • 与Visit对应：从其他的状态-动作对开始一个episode，但其轨迹能经过当前的状态-动作对

🟦MC ε-Greedy

Exploring Starts在实际中难以实现，考虑引入soft policy：随机（stochastic）选择动作

ε-Greedy策略：
$$\pi (a|s)=\{\begin{array}{ll}1-\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1),& \text{for the greedy action, }\\ \frac{\epsilon }{|\mathcal{A}(s)|},& \text{for other }|\mathcal{A}(s)|-1\text{ actions.}\end{array}$$
其中，$\epsilon \in [0,1]$，$|\mathcal{A}(s)|$表示状态$s$下的动作数量。

• 直观理解：以较高概率选择贪心动作（greedy action），以较低均等概率选择其他动作
• 特性：选择贪心动作的概率永远不低于选择其他动作的概率
• 目的：平衡exploitation（探索）和exploration（利用）
  • $\epsilon =0$：侧重于利用，永远选择贪心动作
  • $\epsilon =1$：侧重于探索，以均等概率选择所有动作（均匀分布）

MC ε-Greedy：在策略提升阶段，求解下式
$${\pi }_{k+1}(s)=\underset{\pi \in {\Pi }_{\epsilon }}{\mathrm{argmax}}\sum _a\pi (a|s)q_{{\pi }_k}(s,a)$$

其中，$\pi \in {\Pi }_{\epsilon }$表示所有ε-Greedy策略的集合。得到的最优策略为：
$${\pi }_{k+1}(a|s)=\{\begin{array}{ll}1-\frac{\epsilon }{|\mathcal{A}(s)|}(|\mathcal{A}(s)|-1),& a=a_k^{\ast },\\ \frac{\epsilon }{|\mathcal{A}(s)|},& a\ne a_k^{\ast }.\end{array}$$

MC ε-Greedy与MC Basic和MC Exploring Starts的区别：

• 后二者求解的范围是$\pi \in \Pi$，即所有策略的集合
• 后二者得到的是确定性策略，前者得到的是随机策略

MC ε-Greedy与MC Exploring Starts的唯一区别在于ε-Greedy策略，因此MC ε-Greedy不需要Exploring Starts。

MC ε-Greedy通过探索性牺牲了最优性，但可以通过设置一个较小的ε（如0.1）进行平衡

• 在实际中，可以为ε设置一个较大的初始值，随着迭代轮数逐渐减小其取值
• ε的值越大，最终策略的最优性越差

最终训练得到的策略，可以去掉ε，直接使用greedy的确定性策略（consistent）。