根据二叉树创建字符串
根据二叉树创建字符串
给你二叉树的根节点 root ,请你采用前序遍历的方式,将二叉树转化为一个由括号和整数组成的字符串,返回构造出的字符串。
空节点使用一对空括号对 "()" 表示,转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

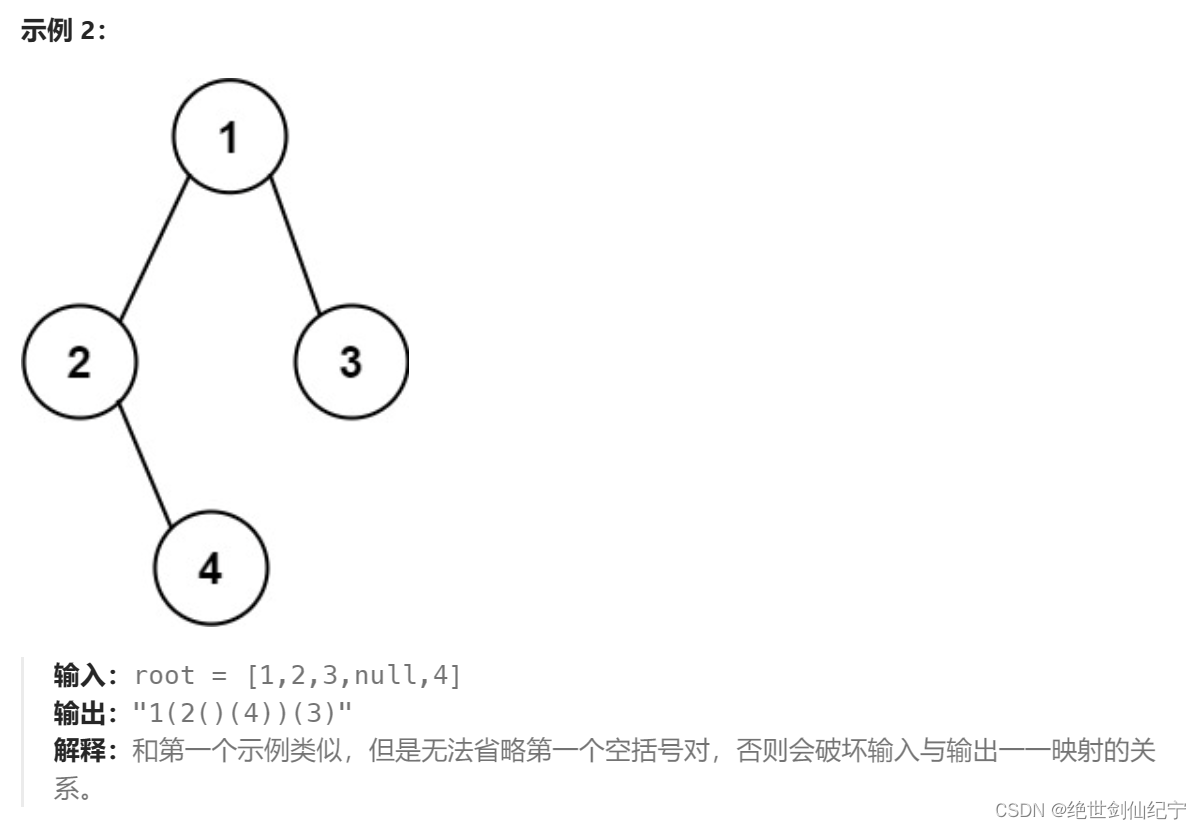
此题使用C++和递归做,其实只有一个难点,就是判断括号何时省略的问题:括号的省略要以不影响树的构建为准。

class Solution {
void PreOrder(TreeNode* root, string & tarstr)
{
tarstr += to_string(root->val);
if(root->left)
{
//左子树不为空,必须加上括号
tarstr += "(";
PreOrder(root->left,tarstr);
tarstr += ")";
}
else if(root->left == nullptr && root->right)
{
// 左子树为空,但右子树不为空
// 不能省略括号
tarstr+="()";
}
if(root->right)
{
// 右子树不为空,当然也不能省略括号
tarstr += "(";
PreOrder(root->right,tarstr);
tarstr += ")";
}
}
public:
string tree2str(TreeNode* root) {
// PreOrder 遍历 中、左、右
string tarstr = "";
PreOrder(root,tarstr);
return tarstr;
}
};二叉树的层序遍历
二叉树的层序遍历
给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
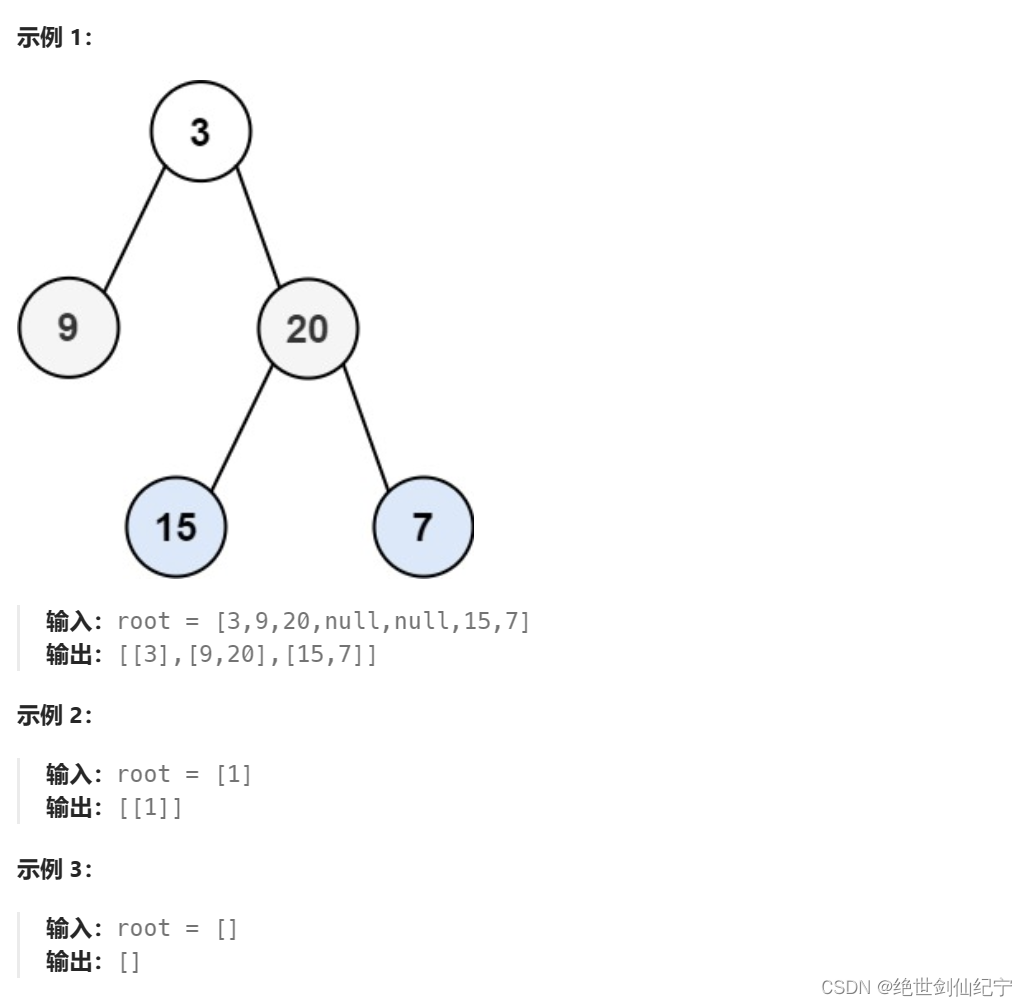
思路: 使用队列来控制层序遍历,采用一个变量 LeverSize 来记录每一层的结点数,根据这个 LeverSize 每一层最为入队和出队数量的依据。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
if(root==nullptr) return vv;
int leverSize = 0;
queue<TreeNode*> que;
que.push(root);
leverSize = 1;
while(!que.empty())
{
vector<int> v1;
while(leverSize--)
{
TreeNode*cur = que.front();
if(cur == nullptr) break;
if(cur->left) que.push(cur->left);
if(cur->right) que.push(cur->right);
int top = cur->val;
v1.push_back(top);
que.pop();
}
leverSize = que.size();
vv.push_back(v1);
}
return vv;
}
};二叉树的最近公共祖先
二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”


思路:将两个结点前序遍历的路径(结点)分别存放在两个栈中,先使两个栈的大小相等,然后各自出栈,确定这两个栈中的第一个相等的栈顶元素,就是他们两个结点最近的公共祖先。
class Solution {
public:
bool PreOrder(TreeNode* root, stack<TreeNode*>& st, TreeNode* tar)
{
if(root == nullptr) return false;
st.push(root);
if(root == tar) return true;
if(PreOrder(root->left,st,tar)==true) return true;
if(PreOrder(root->right,st,tar)==true) return true;
//走到此处,说明左右子树都为空或者找不到
st.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> st1, st2;
TreeNode* cur = root;
PreOrder(root, st1, p);
PreOrder(root, st2, q);
while(st1.size()!=st2.size())
{
if(st1.size()>st2.size()) st1.pop();
else st2.pop();
}
while(st1.top()->val != st2.top()->val)
{
st1.pop();
st2.pop();
}
return st1.top();
}
};二叉搜索树与双向链表
二叉搜索树与双向链表
题目描述
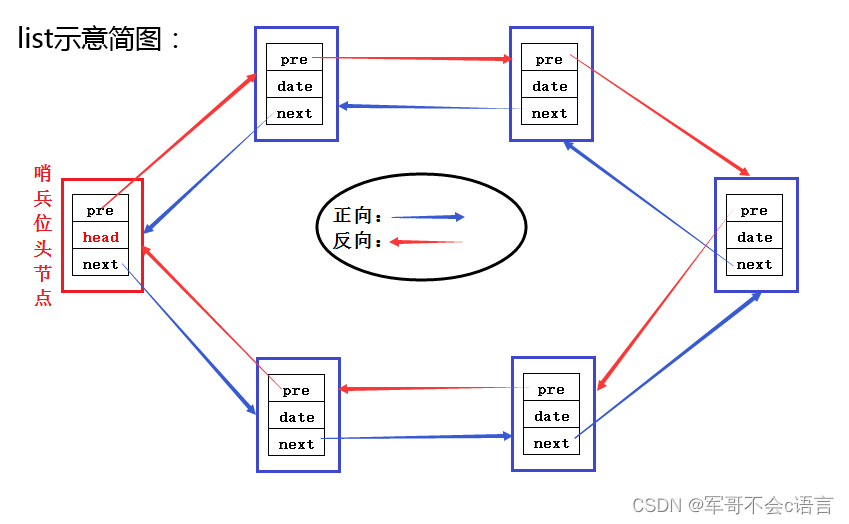
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。如下图所示

 注意:
注意:
1.要求不能创建任何新的结点,只能调整树中结点指针的指向。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继
2.返回链表中的第一个节点的指针
3.函数返回的TreeNode,有左右指针,其实可以看成一个双向链表的数据结构
4.你不用输出双向链表,程序会根据你的返回值自动打印输出
输入描述:二叉树的根节点
返回值描述:双向链表的其中一个头节点。


思路:依据中序遍历的思路,定义一个前驱结点 prev,作为每次中序遍历访问结点的前一个结点,将 prev 的 right 指向当前结点,当前结点的 left 指向 prev。由于中序遍历搜索二叉树,肯定是升序的顺序,那么前驱 prev 与 中序遍历访问的结点结合,便能很好的链接在一起。
class Solution {
public:
void PreOrder(TreeNode* root, TreeNode*& prev)
{
if(root == nullptr) return;
PreOrder(root->left, prev);
root->left = prev;
if(prev) prev->right = root;
prev = root;
PreOrder(root->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
TreeNode* prev = nullptr;
PreOrder(pRootOfTree,prev);
TreeNode* head= pRootOfTree;
while(head && head->left)
{
head = head->left;
}
return head;
}
};