在构建我们的网络时，我们需要用到卷积层提取特征，来看到一些特别的东西，当图片经过卷积层，图片尺寸一般会变化。

当我们构建网络时，我们需要确定各个层的参数，而这些参数，则是要提前计算的，当某些参数发生错误时，那么构建的网络也很可能发生错误。

来看这样一组代码：

>>> import torch>>> import torch.nn as nn>>> conv2=nn.Conv2d(in_channels=3,out_channels=6,kernel_size=5)

这里我们构建了一个卷积层，叫做conv2，同时，我们指定了三个参数，分别为输入通道为3，输出通道（所使用卷积核的个数）为6，卷积核的尺寸为5x5

下面输入图片数据。看看图片数据经过卷积层后尺寸如何变化。

>>> img=torch.randn([1,3,28,28])>>> img.size()torch.Size([1, 3, 28, 28])
>>> img2=conv2(img)>>> img2.size()torch.Size([1, 6, 24, 24])

我们的图片有RGB三个通道，经过卷积层后通道数变为了6个，同时高和宽由28x28变为了24x24

再看下面一组代码：​​​​​​​

>>> conv1=nn.Conv2d(in_channels=3,out_channels=6,kernel_size=5,stride=1,padding=0)>>> img1=conv1(img)>>> img1.size()torch.Size([1, 6, 24, 24])

新的卷积层比原来的卷积层多了两个参数，分别为stride(步长）和padding（填充）。然而，同样的图片经过卷积层conv1和经过卷积层conv2结果相同。

当然，这没什么奇怪的，尽管在conv2中我们并没有指定stride和padding，但pytorch中nn.Conv2d()中参数stride和padding分别默认为1和0。所以才有这种结果。

既然卷积操作是设定的，那么一定存在计算数据经过卷积层后的尺寸变化公式。

公式很简单，就是这样：

若进入卷积层的数据尺寸为正方形：则

• 假设输入特征的大小为n x n

• 假设卷积核的大小为 f x f

• 令padding为p，步长stride为s

• 则输出特征图的大小为 O = ( n - f + 2p )/s + 1

若进入卷积层的数据尺寸为非正方形：则

• 假设输入特征的大小为 nh x nw

• 假设卷积核的大小为 fh x fw

• 令padding为p，步长stride为s

• 则输出特征图的高度为 Oh = (nh - fh + 2p)/s + 1

• 输出特征图的宽度为 Ow = (nw - fw + 2p)/s + 1

再次回到上面的数据：​​​​​​​

>>> img=torch.randn([1,3,28,28])>>> img.size()torch.Size([1, 3, 28, 28])

图片的高和宽分别为28x28，

则输出特征图的大小为：（28-5+0）/1+1=24​​​​​​​

>>> conv1=nn.Conv2d(in_channels=3,out_channels=6,kernel_size=5,stride=1,padding=0)>>> img1=conv1(img)>>> img1.size()torch.Size([1, 6, 24, 24])

再次解释一下图像为什么从3通道变为了6通道：

原因就是我们使用了6个卷积核，每个卷积核（通道数为图片通道数）是对图片（含3个通道）操作的，每个卷积核对图片操作后，输出结果通道变为1，6个卷积核也就是最后得到的通道数为6，也就是得到了6个特征图。

下面是一个卷积核对一张RGB三通道图片的卷积操作：

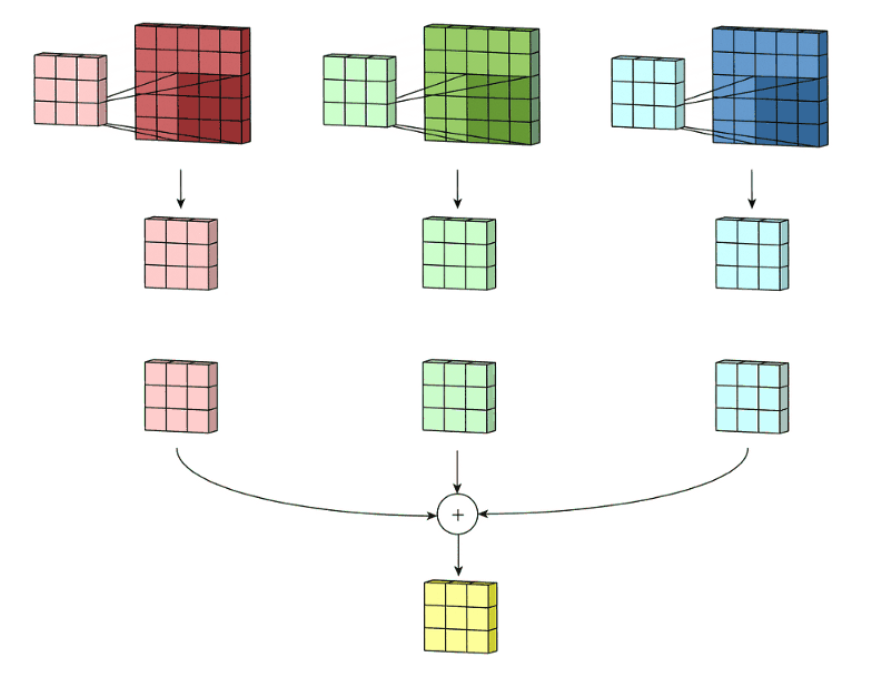
很明显，卷积核通道数与图片通道数（RGB)相同，对每个通道卷积后合并得到最终只有一个通道的特征图。

当然，nn.Conv2d()含有许多参数，并非只有这几个，但这几个在网络的构建中是必不可少的，在许多情况下是足够用的。

更详细的可以看pytorch官方文档：https://pytorch.org/