讲了这么多数据结构相关的知识(可以看我的数据结构文章专栏):
抓紧刷题巩固一下了
目录
1.单值二叉树
题目描述
思路1
代码1
思路2
代码2
2.相同的树
题目描述
思路
代码
3.二叉树的前序遍历
代码
思路
1.单值二叉树
965. 单值二叉树 - 力扣(LeetCode)
题目描述

思路1
利用递归:
首先检查根与左右节点的值是否相等,如果不相等就能直接返回false ,都一样就依次进入左右子树开始检查子树。
对于每个节点,它会检查其左子节点和右子节点的值是否与当前节点的值相同,如果不同则返回 false。如果左右子树都满足条件,则继续递归地检查左子树和右子树
递归的终止条件是当遍历到叶子节点时,此时返回 true
代码1
bool isUnivalTree(struct TreeNode* root) {
if(root==NULL)
return true;
if(root->left!=NULL&&root->left->val!=root->val)
{
return false;
}
if(root->right!=NULL&&root->right->val!=root->val)
{
return false;
}
return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
思路2
首先检查根节点是否为空,如果为空则直接返回 true
然后,代码会递归地检查左子树和右子树。对于每个节点,它会检查其左子节点和右子节点的值是否与当前节点的值相同,如果不同则返回 false。同时,它也会递归地检查左子树和右子树是否为unival树(一旦不满足条件,直接返回false)
满足了就走到最后,返回true
代码2
bool isUnivalTree(struct TreeNode* root) {
if(root==NULL)//看根
{
return true;
}
if(root->left)//左子树不为空就先看左子树符合否
{
if(root->left->val!=root->val||!isUnivalTree(root->left))
return false;
}
if(root->right)//右子树不为空
{
if(root->right->val!=root->val||!isUnivalTree(root->right))
return false;
}
return true;
}2.相同的树
100. 相同的树 - 力扣(LeetCode)
题目描述
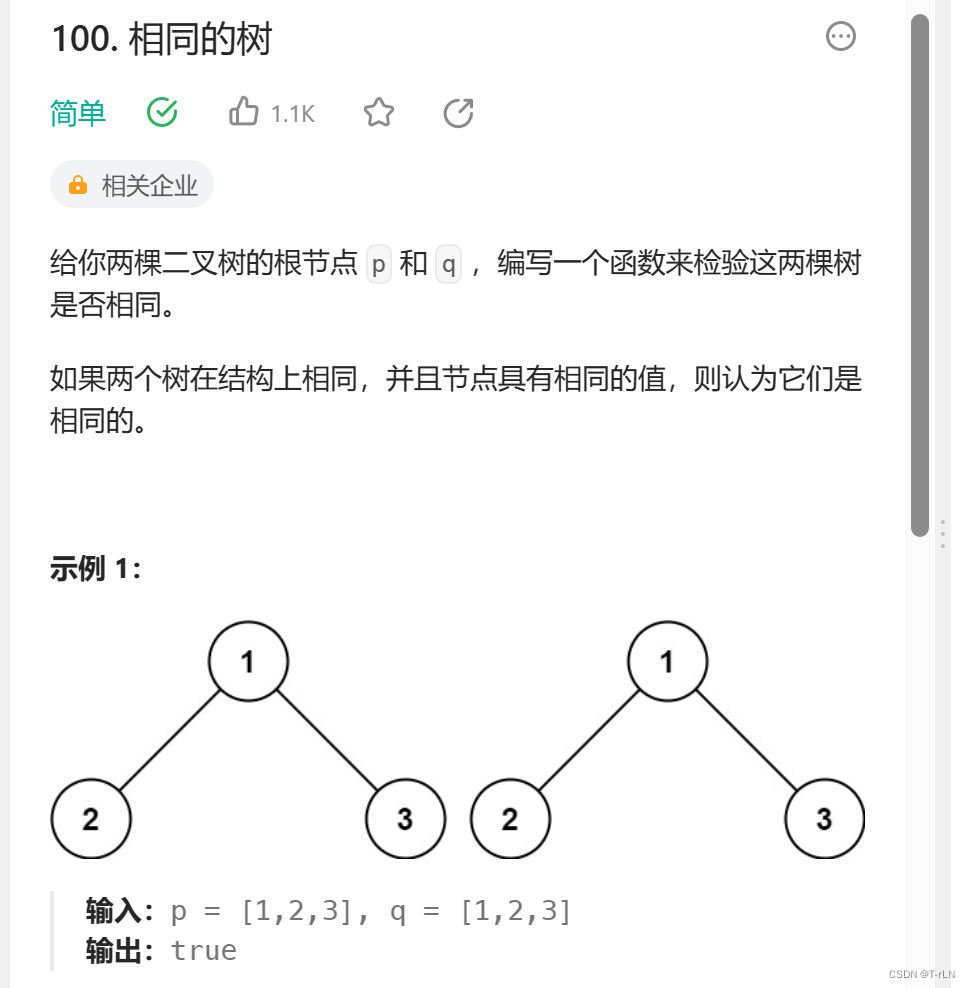
思路
先根和根比,比完再比左子树和右子树
1. 两者都是空时也相等
2. 左节点或右节点一个存在一个不存在返回false;都存在不相等也是false
3.开始递归,都是NULL时返回true或者返回false停止
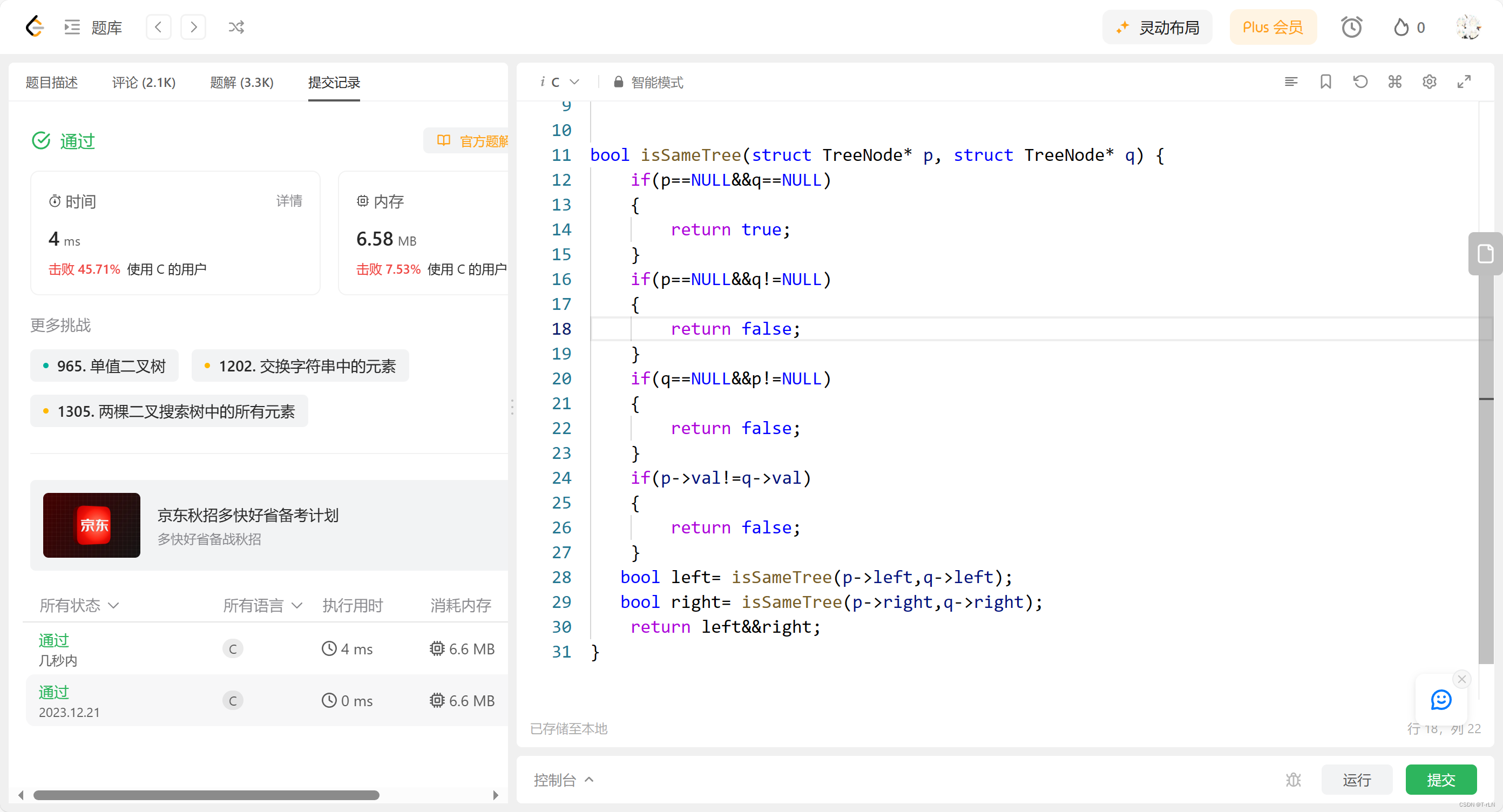
代码
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
if(p==NULL&&q==NULL)
{
return true;
}
if(p==NULL&&q!=NULL)
{
return false;
}
if(q==NULL&&p!=NULL)
{
return false;
}
if(p->val!=q->val)
{
return false;
}
bool left= isSameTree(p->left,q->left);
bool right= isSameTree(p->right,q->right);
return left&&right;
}
3.二叉树的前序遍历
144. 二叉树的前序遍历 - 力扣(LeetCode)
代码
int TreeSize(struct TreeNode* root)
{
return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}
void preorder(struct TreeNode* root, int* a, int* i)
{
if (root == NULL)
{
return;
}
a[*i] = root->val;
(*i)++;
preorder(root->left, a, i);
preorder(root->right, a, i);
}
int* preorderTraversal(struct TreeNode* root, int* returnSize) {
int n = TreeSize(root);
*returnSize=n;
int* a=(int*)malloc(sizeof(int)*n);
int i=0;
preorder(root,a,&i);
return a;
}思路
1.首先题目要求放到malloced的数组里,那就要考虑大小的问题,最后还是运用TreeSize来求一下树里元素的数量比较好,求出来后直接赋值给*returnsize
2.一般使用递归,但是我们已经在函数里面动态开辟了,递归每次调用会消耗很多,最好的办法还是在构建一个函数来进行前置遍历和放入的操作。
3.考虑到参数设置问题,root要有,数组a也要有。那想到需要一个下标才能确保递归时正确放到位置,这个下标还不能在递归函数里面定义,那样没用(都是新的,独立的变量)。
所以要作为参数传入的同时还能保证递归时改变的都是同一个变量那就有两种方法:
- 全局变量
- 传入地址:地址虽然也是临时拷贝,但是都是指向同一块区域