记忆化搜索，可以理解为带备忘录的递归，方便进行剪枝，是一种以空间换时间的策略。

1.斐波那契数

斐波那契数

class Solution {
public://递归
    int fib(int n) {
        return dfs(n);
    }
    int dfs(int n)
    {
        if(n==0 || n==1) return n;
        return dfs(n-1)+dfs(n-2);
    }
};

class Solution {
    int memo[31];
public://递归+记忆化搜索
    int fib(int n) {
        memset(memo,-1,sizeof memo);
        return dfs(n);
    }
    int dfs(int n)
    {
        if(memo[n]!=-1) return memo[n];
        if(n==0 || n==1)
        {
            memo[n] = n;
            return memo[n];
        }
        memo[n] =dfs(n-1)+dfs(n-2);
        return memo[n];
    }
};

class Solution {
public://动态规划
    int fib(int n) {
        int dp[31];
        dp[0] = 0;
        dp[1] = 1;
        for(int i=2;i<=n;i++)
        {
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

从上面可以看出，当出现大量重复的子问题时候，递归转记忆化搜索才有意义，另外，从上面可浅浅的看出，记忆化搜索是一种类型的动态规划，这也是<<算法导论>>这本书里写的，不过，并不是所有的记忆化搜索都能转成动态规划，这是因题而异的，下面的第4和5题就不适合将记忆化搜索转成动态规划。

2.不同路径

不同路径

class Solution {
public://记忆化搜索
    int uniquePaths(int m, int n) {
        vector<vector<int>> memo(m+1,vector<int>(n+1,0));//备忘录
        return dfs(m,n,memo);
    }
    int dfs(int i,int j,vector<vector<int>>& memo)
    {
        if(memo[i][j]!=0) return memo[i][j];
        if(i==0 || j == 0) return 0;
        if(i == 1&& j == 1)
        {
            memo[i][j] = 1;
            return memo[i][j];
        }
        memo[i][j] = dfs(i-1,j,memo) + dfs(i,j-1,memo);
        return memo[i][j];
    }
};

class Solution {
public://动态规划
    int uniquePaths(int m, int n) {
        //状态表示：从起点到(m,n)有多少种不同的路径
        vector<vector<int>> dp(m+1,vector<int>(n+1,0));
        dp[1][1] = 1;
        for(int i=1;i<=m;i++)
        {
            for(int j=1;j<=n;j++)
            {
                if(i==1 && j==1) continue;
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }
        return dp[m][n];
    }
};

3.最长递增子序列

最长递增子序列

class Solution {
public://记忆化搜索
    int lengthOfLIS(vector<int>& nums) {
        int ret = 0;
        int n = nums.size();
        vector<int> memo(n);//备忘录
        for(int i=0;i<n;i++)
        {
            ret = max(ret,dfs(nums,i,memo));
        }
        return ret;
    }
    //dfs作用：以nums[i]为起点的最长递增子序列的长度
    int dfs(vector<int>& nums,int pos,vector<int>& memo)
    {
        if(memo[pos]!=0) return memo[pos];
        int ret = 1;
        for(int i=pos+1;i<nums.size();i++)
        {
            if(nums[i]>nums[pos])
            {
                ret = max(ret,dfs(nums,i,memo)+1);
            }
        }
        memo[pos] = ret;
        return memo[pos];
    }
};

class Solution {
public://动态规划
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        int ret = 0;
        //以nums[i]为起点的最长递增子序列的长度
        vector<int> dp(n,1);
        //从右往左填
        for(int i = n-1;i>=0;i--)
        {
            for(int j = i+1;j<n;j++)
            {
                if(nums[j]>nums[i])
                {
                    dp[i] = max(dp[i],dp[j]+1);
                }
            }
            ret = max(ret,dp[i]);
        }
        return ret;
    }
};

从执行时间上来看，这题使用动态规划来解决并不是最优解，用我们之前在贪心里记录的贪心+二分查找来解决更好。

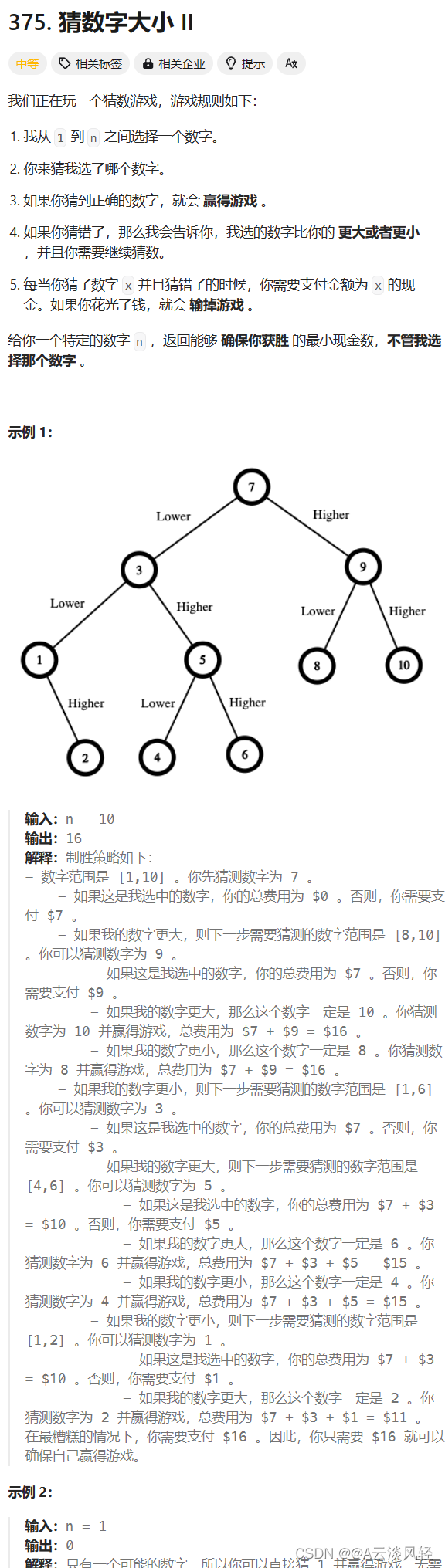
4.猜数字大小II

猜数字大小II

class Solution {
    int memo[202][202];
public://解题方法：暴搜+记忆化搜索
    int getMoneyAmount(int n) {
        return dfs(1,n);
    }
    //dfs的作用：在区间[i,n],不管你选择区间中的哪个数，我都能获胜的最小现金数
    int dfs(int left,int right)
    {
        if(memo[left][right]!=0) return memo[left][right];
        if(left>=right) return 0;
        int ret =INT_MAX;
        for(int head = left;head<=right;head++)//选择头结点
        {
            int x = dfs(left,head-1);
            int y = dfs(head+1,right);
            ret = min(ret,max(x,y)+head);
        }
        memo[left][right] = ret;
        return ret;
    }
};

5.矩阵中的最长递增路径

矩阵中的最长递增路径

class Solution {
    int memo[201][201];
    int dx[4] = {0,0,1,-1};
    int dy[4] = {1,-1,0,0};
    int m,n;
public:
    int longestIncreasingPath(vector<vector<int>>& matrix) {
        m = matrix.size(), n = matrix[0].size();
        int ret = 0;
        for(int i=0;i<m;i++)
        {
            for(int j=0;j<n;j++)
            {
                ret = max(ret,dfs(matrix,i,j));
            }
        }
        return ret;
    }
    //dfs作用：以(i,j)为起点的最长递增路径的长度
    int dfs(vector<vector<int>>& matrix,int i,int j)
    {
        if(memo[i][j]!=0) return memo[i][j];
        int ret = 1;
        for(int k=0;k<4;k++)
        {
            int x = i+dx[k],y = j+dy[k];
            if(x>=0 && x<m && y>=0 && y<n && matrix[x][y]>matrix[i][j])
            {
                ret = max(ret,dfs(matrix,x,y)+1);
            }
        }
        memo[i][j] = ret;
        return ret;
    }
};

leetcode关于递归的题在这就告一段落啦，希望大家通过前面的学习，能力已经有所提高，我们下次再会！