一、题目
1、题目描述
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例1:
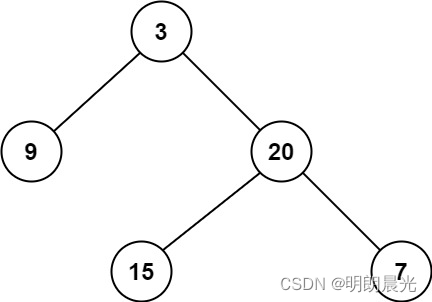
输入:root = [3,9,20,null,null,15,7]
输出:2
示例2:
输入:root = [2,null,3,null,4,null,5,null,6]
输出:5
2、基础框架
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
}
};
3、原题链接
111. 二叉树的最小深度
二、解题报告
1、思路分析
利用Morris遍历的改写的要点:
【麻烦的地方】
Morris遍历有修改指针的情况
【需要解决的问题】
- cur来到哪个节点,正确地记录该节点所在的层level
- 正确地发现叶节点
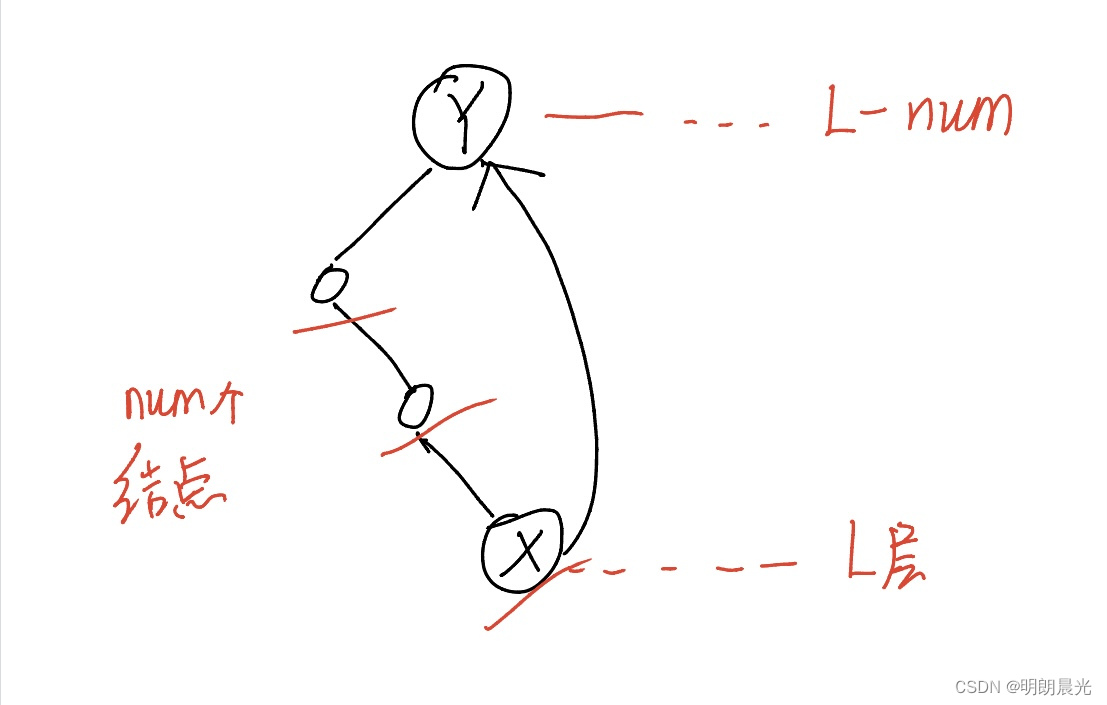
【1、假设刚遍历过的X节点在第 L 层,现在遍历到Y节点,那么Y节点在第几层呢?】
如果Y节点是X的左孩子,则Y在第L + 1层;如果Y是X的右孩子,则Y不一定在L + 1层,因为可能是X修改后的指针指向Y。
所以这样判断:
- 如果Y的左树最右节点不是X,则Y一定在第 L + 1 层;
- 若Y左树的最右节点是X(一定是X的指针修改指向了Y),得到Y左树右边界的节点个数num,然后Y所在的层就是 L - num
【2、如何发现所有的叶节点】
对于能两次访问到的节点,第二次访问结束后,恢复了指针指向后判断是否为叶节点。即不是到某一个节点判断它是否为叶子节点,而是根据上边回到一个节点的时候,反过来看有没有叶子节点。
Morris遍历结束后,最后还要看看整棵树的最右节点是不是叶节点。
【整个流程举例说明】
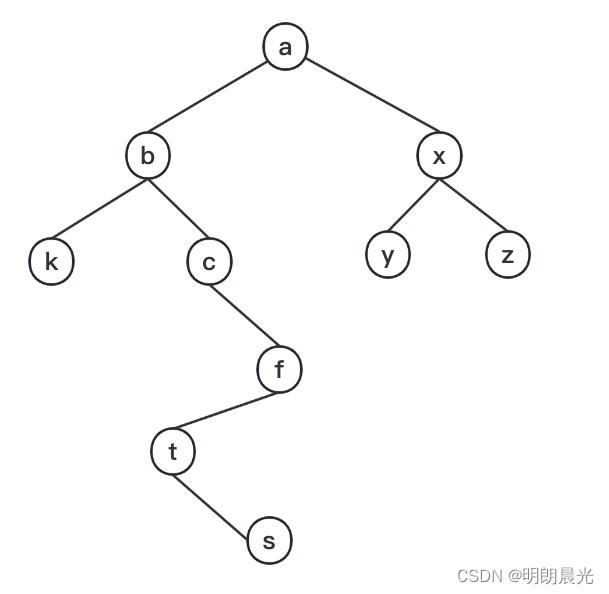
设置变量,一开始:之前遍历到的节点pre = a,所在层数level = 0,最小深度minH = 系统最大。
开始Morris遍历:
- 来到
a节点的时候,a 节点左树的最右节点是 f,f 不等于之前遍历到的节点pre = a,所以 a 在第 1 层;因为是第1次来到 a 节点,所以不去发现叶节点,时机未到,此时 f 右指针指向 a。【pre = a,level = 1, minH = 系统最大】 - 接下来到 b 节点,b 左树最右节点是 k,k ≠ a,所以b一定在第 2 层;又是第1次来到b节点,所以不去发现叶节点,此时修改 k 的右指针指向 b。【pre = b,level = 2, minH = 系统最大】
- 来到 k 节点,k 左树的最右节点为空,不等于 b,所以 k 一定在第3层;且k只能到自己1次,所以也不去发现任何叶节点。【pre = k,level = 3,minH = 系统最大】
- 然后顺着k的右指针回到 b,b的左树最右节点k 等于上一个遍历到的节点pre = k,就知道是从底层上来到,修正 b 所在的层数:level - 左树右边界的长度 = 3 - 1 = 2;又因为是第2次回到b,恢复k的右指针指向空,又因为知道b所在的层数,所以能知道k所在的层数 = b的层数 + 1,且k是叶节点,所以minH = 3。【pre = b,level = 2, minH = 3】
- 来到 c 节点,c 左树的最右节点为空,不等于b,所以 c 一定在第 3 层,且因为是第1次来到c,也不用去结算叶节点;【pre = c,level = 3, minH = 3】
- 来到 f 节点,f 左树的最右节点 s 不等于 c,所以 f 一定在第 4 层,因为是第一次来到 f,不用去结算叶节点,修改 s 的右指针指向 f;【pre = f,level = 4, minH = 3】
- 来到 t 节点,t 左树的最右节点为空,不等于 f,所以 t 一定在第 5 层,且是第一次来到 t,不用结算叶节点;【pre = t,level = 5, minH = 3】
- 来到 s 节点,s 左树的最右节点为空,不等于 t,所以 s 一定在第 6 层,且是第一次来到 s,不用结算叶节点;【pre = s,level = 6, minH = 3】
- 回到 f 节点,f 左树的最右节点 s,等于之前遍历的节点pre,知道是从底层上去的,修正 f 所在的层数 = level - 左树右边界节点数 = 6 - 2 = 4,是第二次来到 f 节点,恢复 s 的右指针指向空,且 s 为叶节点,根据 f 所在的层数算出 s 所在的层数 = f 所在层数+ 2=6,6 >minH = 3,所以minH保持3不变;【pre = f,level = 4, minH = 3】
- 顺着 f 回到 a 节点,a 左树最右节点 f = pre,知道是从底层上去的,修正 a 所在的层数 = level - a左树右边界节 点数 = 4 - 3 = 1,是第二次来到 a 节点,恢复 f 的右指针指向空,而 f 不为叶节点,所以不用更新minH。【pre = a, level = 1,minH = 3】
- …
- 完成Morris遍历后,要看整棵树的最右节点是否为叶节点,如果为叶节点要结算出它的深度,与minH进行比较。
2、时间复杂度
O ( N ) O(N) O(N)
3、代码详解
- 方法一:二叉树的递归套路
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int minDepth(TreeNode* root) {
if (root == nullptr) return 0;
return p(root);
}
//返回以x为头的树的最小深度
//时间复杂度O(N),空间复杂度O(树的高度)
int p(TreeNode *x) {
//左右子树都为空,则为叶子节点
if (x->left == nullptr && x->right == nullptr) {
return 1;
}
//左右子树起码有一个不为空
int leftH = INT_MAX;
if (x->left != nullptr) {
leftH = p(x->left); //得到左树的最小深度
}
int rightH = INT_MAX;
if (x->right != nullptr) {
rightH = p(x->right); //得到右树的最小深度
}
return 1 + min(leftH, rightH);
}
};
- 方法二:根据Morris遍历改写
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
//Morris遍历的解
int minDepth(TreeNode* root) {
if (root == nullptr) return 0;
TreeNode *cur = root;
TreeNode *mostRight = nullptr;
int curLevel = 0;
int minH = INT_MAX;
while (cur != nullptr) {
mostRight = cur->left;
if (mostRight != nullptr) {
int rightBoardSize = 1;
while (mostRight->right != nullptr && mostRight->right != cur) {
rightBoardSize++;
mostRight = mostRight->right;
}
if (mostRight->right == nullptr) { //第一次到达cur
curLevel++;
mostRight->right = cur;
cur = cur->left;
continue;
} else {//第二次到达cur
if (mostRight->left == nullptr) { //cur左树的最右节点为叶节点
minH = min(minH, curLevel);
}
curLevel -= rightBoardSize; //修正cur的层数
mostRight->right = nullptr;
}
} else { //只能到达一次
curLevel++;
}
cur = cur->right;
}
//判断整棵树的最右节点是否为叶节点
int finalRight = 1;
cur = root;
while (cur->right != nullptr) {
finalRight++;
cur = cur->right;
}
if (cur->left == nullptr && cur->right == nullptr) {
minH = min(minH, finalRight);
}
return minH;
}
};
两个方法的Java版代码:
// 本题测试链接 : https://leetcode-cn.com/problems/minimum-depth-of-binary-tree/
public class MinDepth {
// 不提交这个类
public static class TreeNode {
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int x) {
val = x;
}
}
// 下面的方法是一般解
public static int minDepth1(TreeNode head) {
if (head == null) {
return 0;
}
return p(head);
}
// 返回x为头的树,最小深度是多少
public static int p(TreeNode x) {
if (x.left == null && x.right == null) {
return 1;
}
// 左右子树起码有一个不为空
int leftH = Integer.MAX_VALUE;
if (x.left != null) {
leftH = p(x.left);
}
int rightH = Integer.MAX_VALUE;
if (x.right != null) {
rightH = p(x.right);
}
return 1 + Math.min(leftH, rightH);
}
// 下面的方法是morris遍历的解
public static int minDepth2(TreeNode head) {
if (head == null) {
return 0;
}
TreeNode cur = head;
TreeNode mostRight = null;
int curLevel = 0;
int minHeight = Integer.MAX_VALUE;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
int rightBoardSize = 1;
while (mostRight.right != null && mostRight.right != cur) {
rightBoardSize++;
mostRight = mostRight.right;
}
if (mostRight.right == null) { // 第一次到达
curLevel++;
mostRight.right = cur;
cur = cur.left;
continue;
} else { // 第二次到达
if (mostRight.left == null) {
minHeight = Math.min(minHeight, curLevel);
}
curLevel -= rightBoardSize;
mostRight.right = null;
}
} else { // 只有一次到达
curLevel++;
}
cur = cur.right;
}
int finalRight = 1;
cur = head;
while (cur.right != null) {
finalRight++;
cur = cur.right;
}
if (cur.left == null && cur.right == null) {
minHeight = Math.min(minHeight, finalRight);
}
return minHeight;
}
}