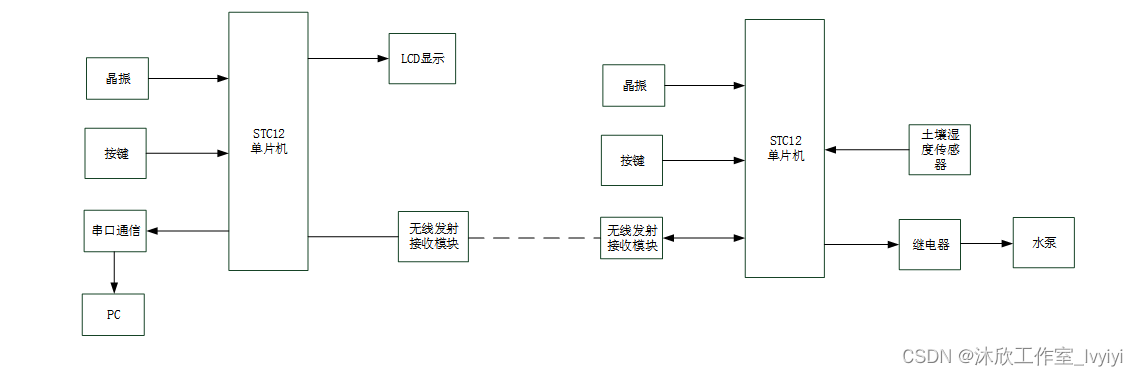
本专栏栏目提供文章与程序复现思路，具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》

这个标题涉及微电网（Microgrid）的双层鲁棒容量规划，考虑了多元不确定性和备用需求。让我们逐步解读这个标题：

1. 微电网（Microgrid）： 微电网是一种小型电力系统，通常由分布式能源资源（如太阳能电池、风力发电机）、储能设备和负载组成。微电网通常是自治的能源系统，可以独立运行或与主电网连接。

2. 双层鲁棒容量规划： 双层鲁棒容量规划是指在规划微电网的能力时考虑到两个层次的不确定性和鲁棒性。鲁棒性表示系统对于外部变化或不确定性的适应能力。这两个层次可能涉及到不同的决策层面，一个可能是整个微电网系统的容量规划，而另一个可能是各个子系统或组件的容量规划。

3. 多元不确定性： 这表示在规划中考虑到了多种不确定性因素。在微电网的情境下，这些因素可能包括天气变化、负载波动、能源资源波动等。考虑到这些因素，制定鲁棒的容量规划能够提高微电网系统的可靠性和稳定性。

4. 备用需求： 这指的是在规划中考虑到了备用能力的需求。备用能力是指系统中的额外能力，可以在主要组件或系统故障时接管。在微电网中，备用需求的考虑可以提高系统的冗余性，使其更能应对突发状况。

因此，整个标题的意义是在微电网规划中，以双层的方式来考虑容量规划，同时关注多元的不确定性因素和备用需求，以确保系统在面临各种不确定性和挑战时仍然能够鲁棒地运行。

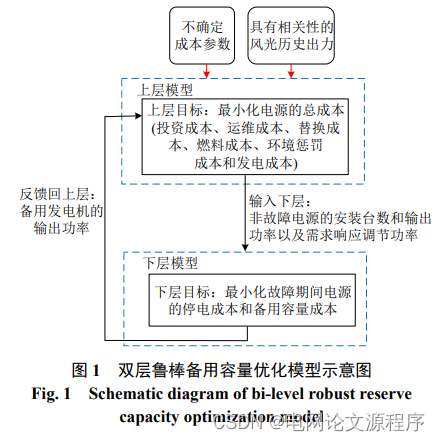
摘要：为了在独立微电网规划过程中综合考虑成本参数、风光资源的不确定性和备用需求，提出了风光储柴双层鲁棒容量规划模型。上层目标为包含投资、替换、运维以及燃料成本、环境惩罚成本和发电成本在内的总净现值成本最小，上层约束中，通过建立成本参数的区间不确定集合考虑了电源成本参数的不确定性以及风光历史出力的凸包不确定集合考虑了风光资源的相关性，同时考虑了需求响应模型对容量规划的影响。下层目标函数为最小化电源故障期间的停电成本和备用成本，下层约束考虑了故障期间备用发电机的出力约束以及备用容量约束。首先，基于库恩塔克(karush-kuhntucker,KKT)条件将下层模型转化为互补约束，利用大M法将下层变成混合整数线性规划(mixedintegerlinear programming,MILP)模型，之后，利用对偶理论将鲁棒单层模型转化为确定性模型。最后，基于实际工程算例，验证所提出的算法能够有效考虑成本参数及风光资源等多元不确定性，同时满足系统备用需求。与遗传算法及其他双层鲁棒组合(直接混合整数二次规划(directmixed-integer quadratic programming,DMIQP)+枚举鲁棒对等(enumeration robust counterpart,ERC)等)算法相比，具有更高的计算效率。 

这段摘要描述了一种用于独立微电网规划的风光储柴双层鲁棒容量规划模型，并详细说明了该模型的设计和求解方法。以下是对摘要的详细解读：

1. 问题背景： 研究的背景是在独立微电网的规划中，考虑成本参数、风光资源的不确定性和备用需求。

2. 提出的模型： 提出了一个风光储柴双层鲁棒容量规划模型。这意味着在规划微电网容量时，同时考虑了风能、光能和储能等多个能源，以及备用发电机的需求。

3. 上层目标和约束： 上层目标是通过最小化总净现值成本来综合考虑投资、替换、运维、燃料成本、环境惩罚成本和发电成本。上层约束包括成本参数的不确定性和风光历史出力的不确定性，同时考虑了需求响应模型对容量规划的影响。

4. 下层目标和约束： 下层目标是最小化电源故障期间的停电成本和备用成本。下层约束包括故障期间备用发电机的出力约束和备用容量约束。

5. 求解方法： 首先，利用库恩塔克(Karush-Kuhn-Tucker, KKT)条件将下层模型转化为互补约束。然后，通过大M法将下层变成混合整数线性规划(MILP)模型。接着，利用对偶理论将鲁棒单层模型转化为确定性模型。

6. 验证： 通过实际工程算例验证了所提出的算法的有效性，证明其能够有效考虑成本参数和风光资源等多元不确定性，并同时满足系统备用需求。

7. 性能比较： 与其他算法（如遗传算法、直接混合整数二次规划+枚举鲁棒对等等）相比，该算法具有更高的计算效率。

总体而言，这个研究提供了一种在微电网规划中综合考虑多个因素的复杂模型和相应的高效求解方法，以实现鲁棒的容量规划。

关键词：    备用容量;凸包不确定集合;时空相关性;双层优化算法;鲁棒优化算法;

解读关键词：

1. 备用容量： 这指的是系统中额外的能力或设备，用于应对主要组件或系统故障的情况。在微电网规划中，考虑备用容量是为了提高系统的可靠性和鲁棒性，以确保在发生故障时依然能够满足电力需求。

2. 凸包不确定集合： 凸包是一个几何概念，表示包含在一组点集合内的最小凸多边形或凸多面体。在这里，凸包不确定集合可能指的是对于某些数据或参数的不确定性，使用凸包来表示这种不确定性的范围或可能性。

3. 时空相关性： 涉及到时序和空间上的相关性，表示系统中不同组件或参数在时间和空间上的相互影响。在微电网规划中，时空相关性的考虑可以更准确地反映系统运行的复杂性和动态性。

4. 双层优化算法： 这是一种优化算法，特指具有两个层次（上层和下层）的优化模型。在微电网规划中，上层通常涉及高层次的决策，而下层则涉及底层的资源配置或操作问题。这种算法能够同时优化这两个层次的目标函数和约束。

5. 鲁棒优化算法： 鲁棒性是指系统对于外部扰动或不确定性的适应能力。因此，鲁棒优化算法旨在考虑不确定性，并设计系统在不确定条件下依然能够保持优化性能。

这些关键词在微电网规划中都具有重要的意义。备用容量、凸包不确定集合和时空相关性的考虑有助于提高系统的鲁棒性。而双层优化算法和鲁棒优化算法则为解决微电网规划中的复杂问题提供了有效的工具和方法。

仿真算例：

本文以某风光储柴独立微电网示范工程为研 究对象，风光全年历史出力数据来自比利时的实际 工程数据，具体数据可参见文献[20]。全年负荷数 据来自美国爱荷华州 240 节点配电网实际数据，具体 数据可参见文献[21]，其中峰值负荷为 2436.199kW。 本文微电网系统从春夏秋冬四季各选取一个 典型日，以典型日 96h 为总规划时间，时间间隔为 1h。常见的折现率主要有 5%[22]、6.7%[23]、8%[6]和 10%[19,24]，本文取 8%。系统运行年限，主要有 10 年[25]、20 年[6,24,26-27]，考虑到技术更新很快且价格 变动大，本文取 10 年。

模型参数包括风光储柴、光伏逆变器和需求响 应负荷的参数。本文选用的风机和光伏类型分别为 陆上风机和分布式光伏，额定容量分别为 11.5kW 和 1kW。采用的储能为铅酸蓄电池，其额定容量为 6kWh，充放电效率均为 86%，蓄电池的自放电率 为 0.01%，初始电量和剩余电量百分比的最大值均 为 100%，最小值为 20%，充放电状态转换次数上 限值为 10 次，储能蓄电池寿命主要有 1.36[28]、 4 [27,29]、5 [30]、6 [22]、10[24,31-32]和 20 年[33]，本文选择 蓄电池寿命为 4 年。

本文采用的柴油发电机燃料曲线的系数 a、b， 分别取 0.280L 和 0.251L/kW，为了减少使用柴油发 电机对环境造成的影响，环境成本应尽可能大，本 文选择 500 元/L。另外，光伏逆变器效率为 97%，总 负荷用于需求响应负荷的比例系数为 10%。 对于单位功率的停电成本和单位容量备用成 本，本文参考文献[34]和文献[35]分别取 0.5832 元/ kW 和 6.3521 元/kW。本文中电源故障率 k 参考 文献[35]的数据，如表 1 所示。

由于大多数文献并未考虑风光柴的替换成本， 本文仅考虑储能的替换成本作为不确定参数，将各 电源的成本参数统一换算，如附录 A 表 A1—A4 所 示。本文共考虑 11 个不确定成本参数，忽略过高 的成本参数，对于风机、光伏和储能的类型有多种， 本文仅选择其中一种进行研究，汇总如表 2 所示。 当不考虑参数的不确定性时，参数取值如表 2 的右 侧所示。

仿真程序复现思路：

对于仿真复现上述文中描述的微电网系统规划问题，可以使用Python编程语言结合相关的优化库（如SciPy、PuLP等）和数据处理库（如Pandas、NumPy等）来实现。下面是一个基本的仿真思路和代码框架，但需要注意的是，这里只是一个示例，具体实现可能需要进一步的细化和优化以满足您的需求。

import pandas as pd
import numpy as np
from scipy.optimize import minimize

# 加载数据
wind_solar_data = pd.read_csv('wind_solar_data.csv')
load_data = pd.read_csv('load_data.csv')

# 模型参数
rated_capacity_wind = 11.5  # kW
rated_capacity_solar = 1  # kW
rated_capacity_storage = 6  # kWh
efficiency_storage = 0.86
self_discharge_rate = 0.01
max_charge_discharge_cycles = 10
storage_lifetime = 4  # years

fuel_curve_coefficients = {'a': 0.280, 'b': 0.251}
fuel_cost = 500  # 元/L

inverter_efficiency = 0.97
demand_response_ratio = 0.1

power_outage_cost = 0.5832  # 元/kW
capacity_reserve_cost = 6.3521  # 元/kW

# 定义优化问题
def cost_function(x):
    # x是待优化的参数向量，例如各种能源的比例、容量等
    # 在这里进行成本计算，考虑不确定性和各种参数
    # 返回成本值作为优化目标

    # 提取优化参数
    ratio_wind = x[0]
    ratio_solar = x[1]
    ratio_storage = x[2]

    # 计算各个能源的容量
    capacity_wind = ratio_wind * rated_capacity_wind
    capacity_solar = ratio_solar * rated_capacity_solar
    capacity_storage = ratio_storage * rated_capacity_storage

    # 计算成本
    total_cost = (
        capital_cost(capacity_wind, 'wind') +
        capital_cost(capacity_solar, 'solar') +
        capital_cost(capacity_storage, 'storage') +
        operational_cost(capacity_wind, wind_solar_data['wind_output']) +
        operational_cost(capacity_solar, wind_solar_data['solar_output']) +
        operational_cost_storage(capacity_storage, wind_solar_data['load'])
    )

    return total_cost

# 定义约束条件函数
def constraint_function(x):
    # 在这里定义优化问题的约束条件，如容量约束、电力平衡等
    # 返回约束条件的值（应该小于等于0才满足约束）

    # 提取优化参数
    ratio_wind = x[0]
    ratio_solar = x[1]
    ratio_storage = x[2]

    # 容量约束
    capacity_constraint = capacity_wind + capacity_solar + capacity_storage - load_data['peak_load'].max()

    # 电力平衡约束
    balance_constraint = sum(wind_solar_data['wind_output'] * ratio_wind +
                             wind_solar_data['solar_output'] * ratio_solar +
                             wind_solar_data['load'] * ratio_storage) - sum(load_data['load'])

    return [capacity_constraint, balance_constraint]

# 定义成本计算函数
def capital_cost(capacity, source):
    # 根据能源类型和容量计算初始投资成本
    # 这里只是一个示例，请根据实际情况修改
    if source == 'wind':
        return capacity * 1000  # 假设风能装机容量的初始投资成本为1000元/kW
    elif source == 'solar':
        return capacity * 1200  # 假设太阳能装机容量的初始投资成本为1200元/kW
    elif source == 'storage':
        return capacity * 500  # 假设储能装机容量的初始投资成本为500元/kWh

def operational_cost(capacity, output_data):
    # 根据能源输出数据和容量计算运营成本
    # 这里只是一个示例，请根据实际情况修改
    return sum(output_data * capacity * 0.08)  # 假设运营成本为每单位能量的8%

def operational_cost_storage(capacity, load_data):
    # 根据负荷数据和储能容量计算运营成本
    # 这里只是一个示例，请根据实际情况修改
    return sum(load_data * capacity * 0.1)  # 假设运营成本为每单位能量的10%

# 定义初始参数猜测值
initial_guess = np.array([0.4, 0.4, 0.2])  # 示例初始参数，根据实际情况调整

# 定义优化器
result = minimize(cost_function, initial_guess, constraints={'type': 'ineq', 'fun': constraint_function})

# 输出优化结果
print("优化结果:")
print(result)

这个示例中包含了更多的细节，包括成本计算、约束条件的定义等。请根据您的实际情况修改这个代码框架。如果您有特定的约束条件或成本模型，需要根据这些具体要求进一步调整代码。