考点分布目录

中央处理单元CPU
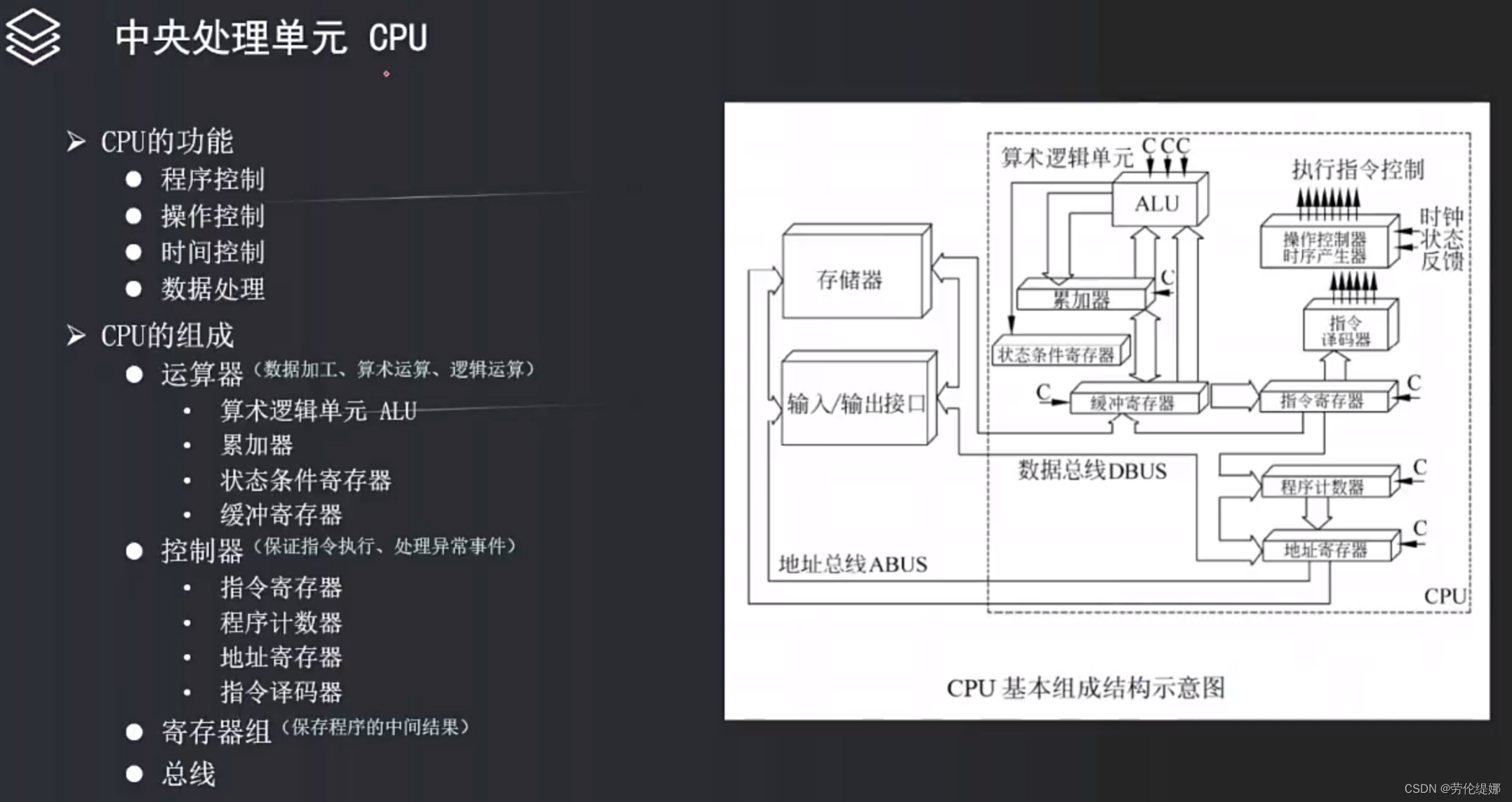
练习题

数据的表示
二进制转十进制

练习题

十进制转二进制

练习题

原码

练习题

反码

练习题
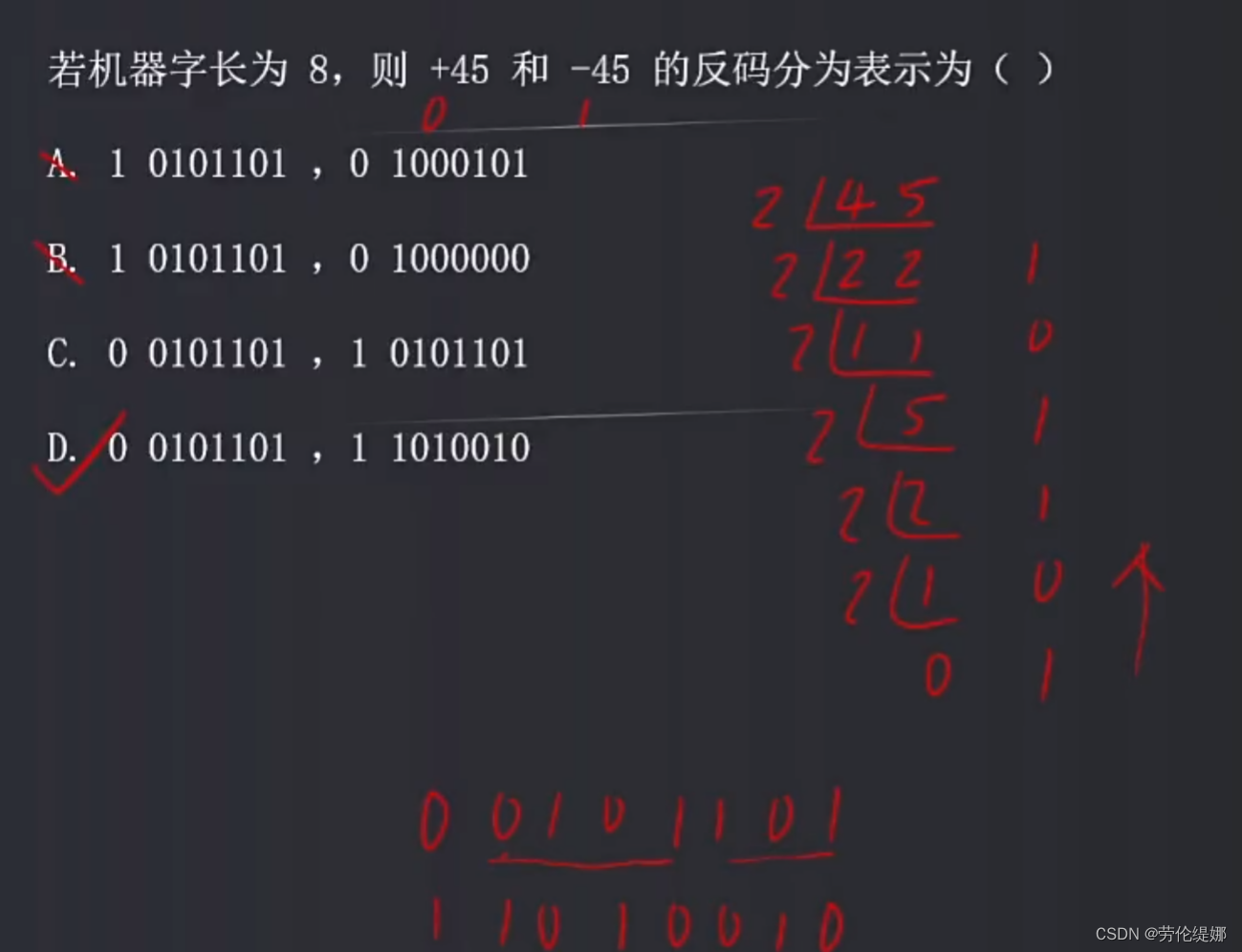
补码

练习题
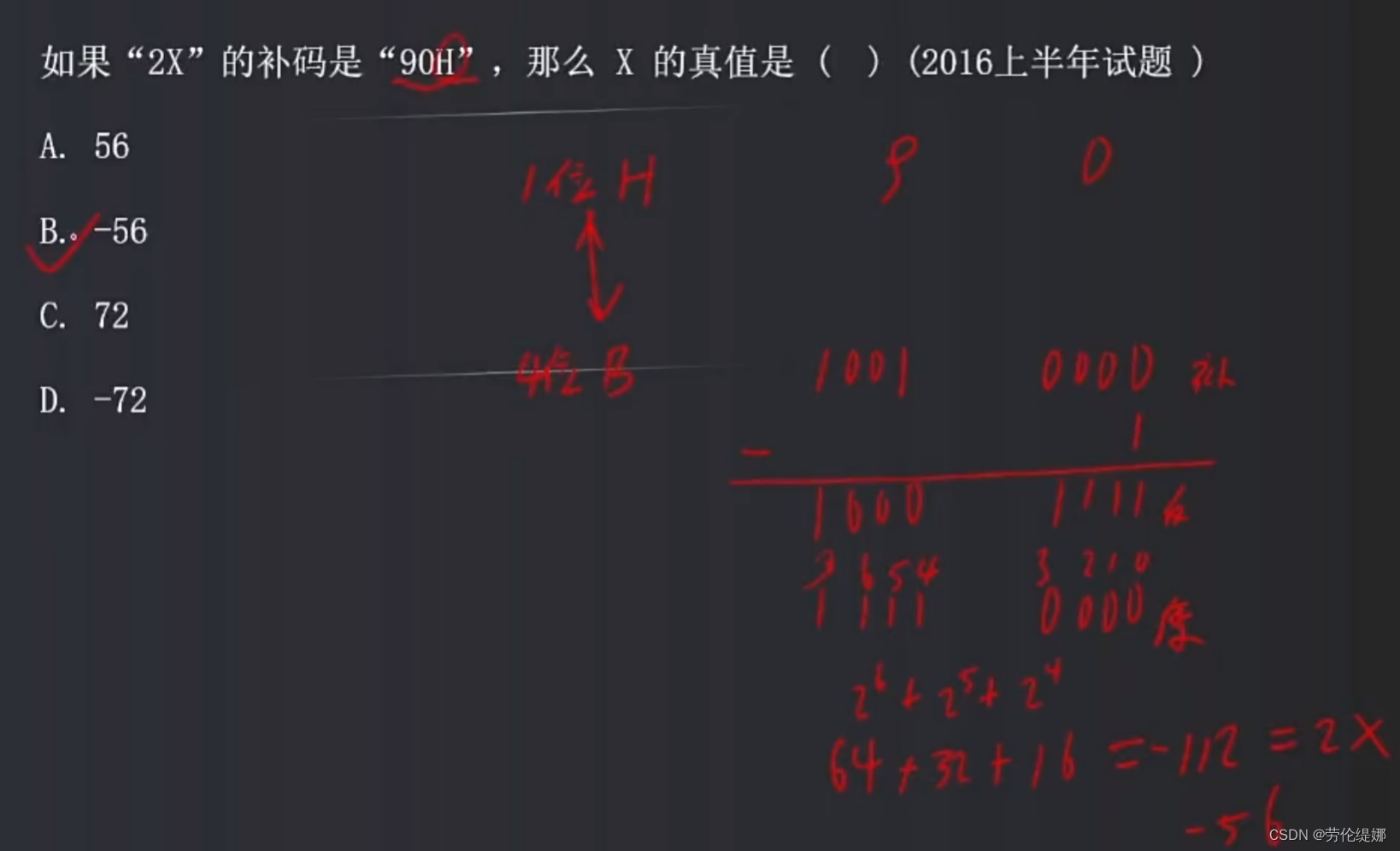
练习题

移码

浮点数

练习题

奇偶校验

练习题
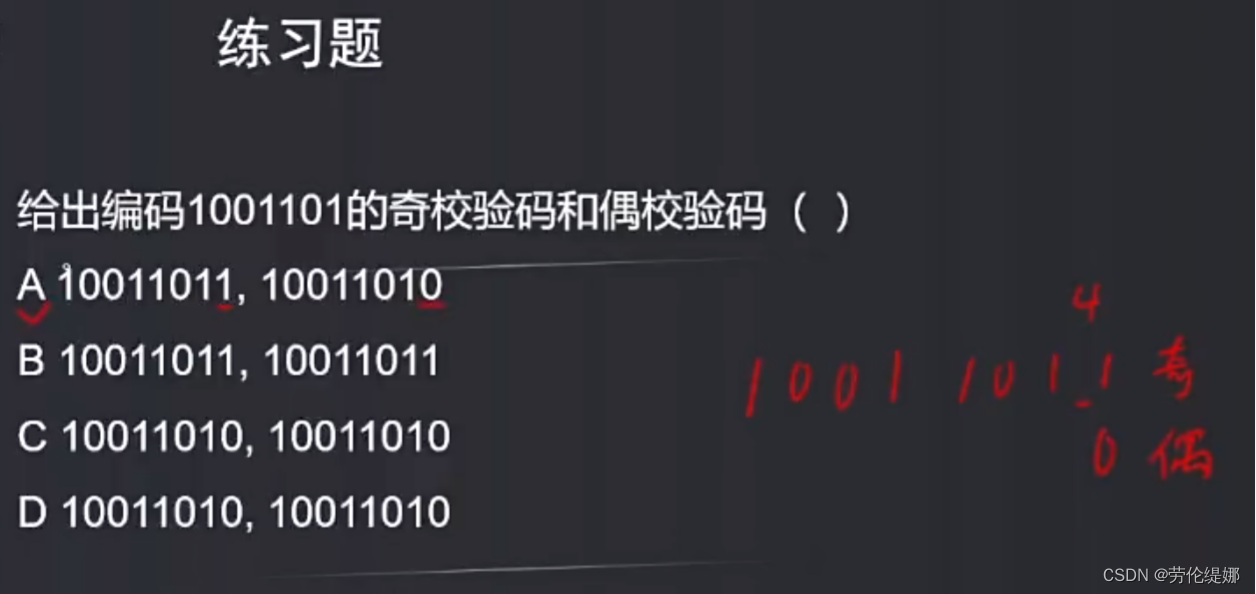
校验码
模2除法
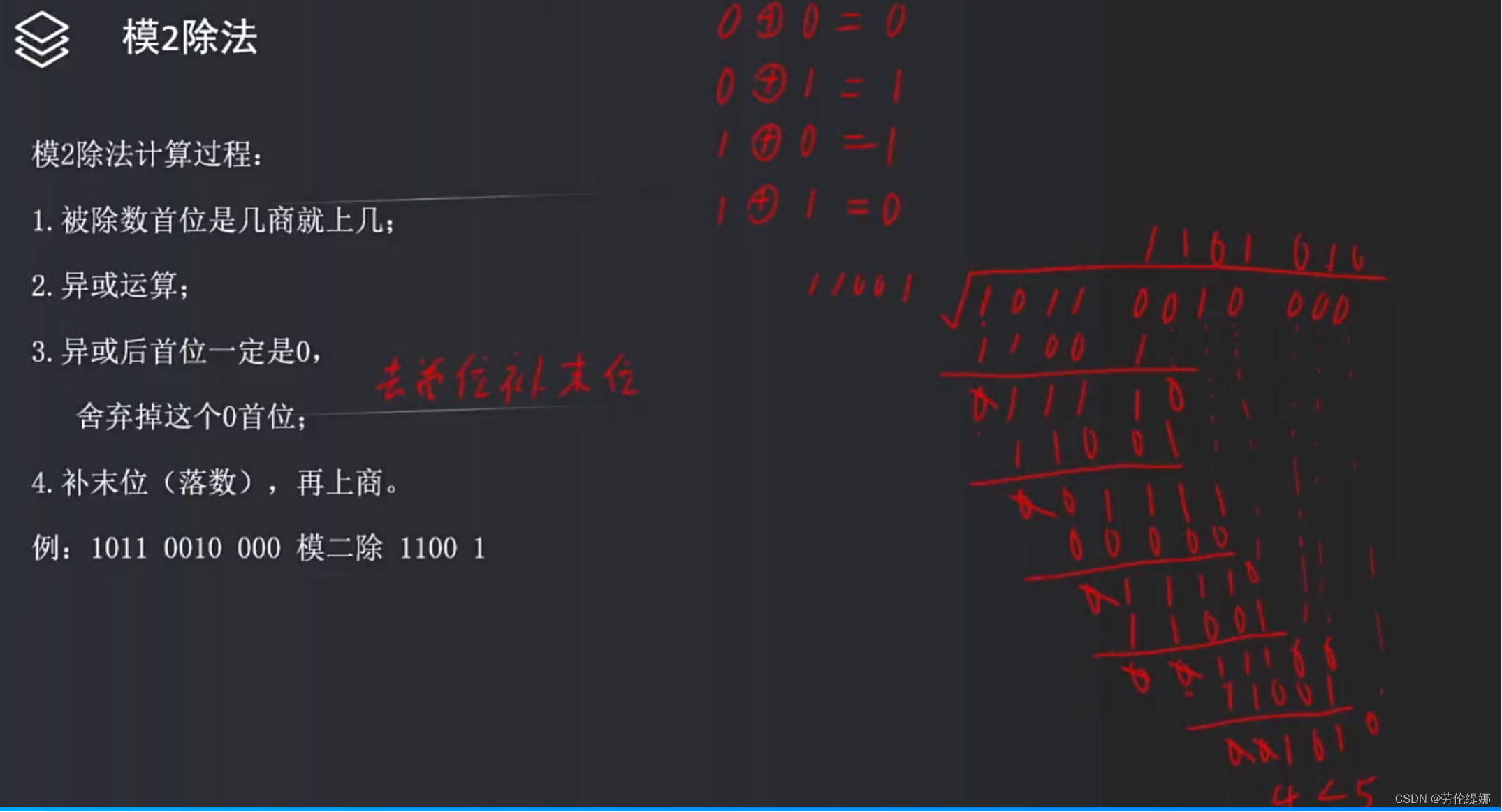
循环冗余校验CRC

练习题

练习题

练习题

奇偶校验码 只能查是否有错误而无法纠错,且要求只能有一位出现错误。
为了能找到发生错误的位置,而有了 海明校验码;
实际上本质来说, 海明码是升级款的奇偶校验码,其采用了一种非常巧妙的方式,把这串数字(即要传输的内容)分了组,通过分组校验来确定哪一位出现了错误,类似KMP算法,描述起来很麻烦,实际上使用起来却很简单
“海明”也被译为”汉明”
海明校验

练习题

实例
数据位为8的数据 D7D6D5D4D3D2D1D0=01101001,求海明码
1.计算校验位的个数
设数据位为n位,校验位P为k位,则n和k必须满足以下关系:
2^k−1≥n+k
此例中有 2k−1≥8+k,可得k最小应为4,即 16 – 1 ≥ 8 + 4。
(奇偶校验称为 Parity Check,Parity Bit即奇偶校验位,故用P表示校验位)
2.计算校验位的位置
2.1 海明码的总位数
设校验位为P,数据位为D,海明码为H,则海明码H的位数为数据的位数和校验码的位数相加,
在此即为 8+4 = 12 位
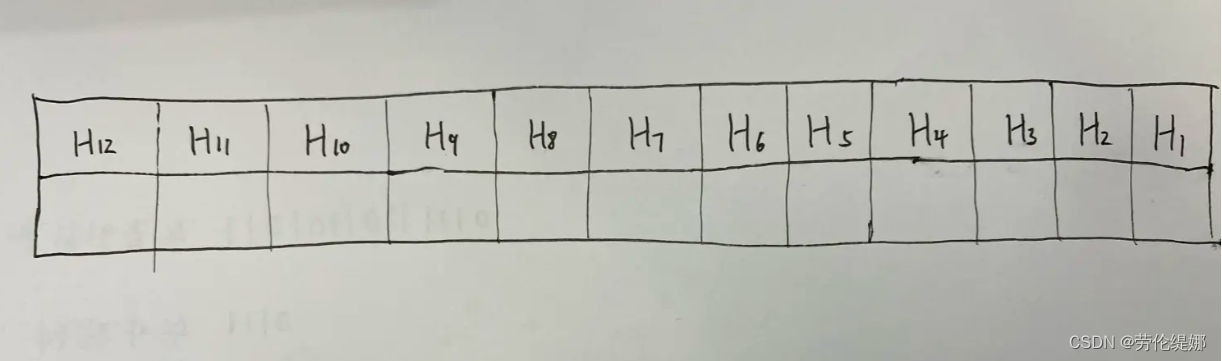
2.2 校验码的位置
校验位P 在海明码的第 2^(i−1)
位,即 Hj=Pi,j=2^(i−1) ,i从1开始计数。
无论是海明码、校验位还是数据位,均从右向左排列,即从低位向高位排列。
可先填入校验码的位置,再将数据位依次从低位到高位填入
如此例,i即为 1,2,3,4, 故有:


3.确定每个数据位 都由哪些校验码进行校验
根据 2^{i-1}的公式,可知 P4、P3、P2、P1的下标分别为8、4、2、1
确定 D0−D7 每个数据位都是由哪些校验码§进行校验的
数据位D的下标,等于其校验位的下标之和

4.计算校验码的值
校验码的值 为有参与校验的数据依次从低到高异或的值。
(异或:相同为0,相异为1)
因为 D7D6D5D4D3D2D1D0=01101001
P1 参与了 D0、D1、D3、D4、D6 等数据位的校验。
P2参与了 D0、D2、D3、D5、D6 等数据位的校验。
P3参与了 D1、D2、D3、D7等数据位的校验。
P4参与了 D4、D5、D6、D7 等数据位的校验。
所以:(D7D6D5D4D3D2D1D0=01101001)
P1=D0⊕D1⊕D3⊕D4⊕D6=1⊕0⊕1⊕0⊕1=1
P2=D0⊕D2⊕D3⊕D5⊕D6=1⊕0⊕1⊕1⊕1=0
P3=D1⊕D2⊕D3⊕D7=0⊕0⊕1⊕0=1
P4=D4⊕D5⊕D6⊕D7=0⊕1⊕1⊕0=0
5.错误校验
确定错误校验 G4G3G2G1,校验码有几位,错误校验就有几位。
如果采用偶校验则结果全为0时没有错误,如果采用奇校验则结果全为1时没有错误
G1=P1D0⊕D1⊕D3⊕D4⊕D6=1⊕1⊕0⊕1⊕0⊕1=0
G2=P2D0、D2、D3、D5、D6=0⊕1⊕0⊕1⊕1⊕1=0
G3=P3D1、D2、D3、D7=1⊕0⊕0⊕1⊕0=0
G4=P4D4、D5、D6、D7=0⊕0⊕1⊕1⊕0=0
则 G4G3G2G1=0000,表示没有异常。假如结果为0100则转为十进制为8,表示第八位存在异常。
海明码是一种纠错码,其方法是为需要校验的数据位增加若干校验位,使得校验位的值决定于某些被校位的数据,当被校数据出错时,可根据校验位的值的变化找到出错位,从而纠正错误。对于32位的数据,至少需要增加( )个校验位才能构成海明码。