本文介绍椭圆曲线密码及其Python实现。
一、实验目的
1、 掌握椭圆曲线上的点间四则运算和常见的椭圆曲线密码算法;
2、 了解基于ECC的伪随机数生成算法和基于椭圆曲线的商用密码算法。
二、算法原理
1、算法简介
椭圆曲线密码学(Elliptic Curve Cryptography,ECC)是一种基于椭圆曲线数学的公开密钥加密算法。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。
ECC的主要优势是在某些情况下它比其他的算法(比如RSA加密算法)使用更小的密钥并提供相当的或更高等级的安全。ECC的另一个优势是可以定义群之间的双线性映射,基于Weil对或是Tate对;双线性映射已经在密码学中发现了大量的应用,例如基于身份的加密。
2、椭圆曲线的数学原理
椭圆曲线(ECC)可以用下述方程表示:
y^^2 = x^^3 + ax + b,其中a、b是实数,椭圆曲线记为E(a,b)。由方程可知,每一条椭圆曲线都关于x轴对称。
1、加法(+):
为了在群上定义加法,参数a和b需要满足不等式4a^^3 + 27b^^2 ≠ 0.加法的运算规则为:若椭圆曲线上的3个点在同一条直线上,则它们的和为O(无穷远点)。
2、减法(-):
点P的负元定义如下:
点P(x,y)的负元是具有相同x坐标和相反的y坐标的点,即若P = (x,y),则-P = (x, -y)。则P和-P可用一条垂直的线连接起来,且P + (-P) = P – P = 0.
P – Q = P + (-Q)。
3、数乘:
n为非负整数,则nP = P + …… + P(n个P相加)。
4、除法:
m为非负整数,则P / m = P * m^^-1,其中m-1为m在模p下的逆元。
3、椭圆曲线加密原理
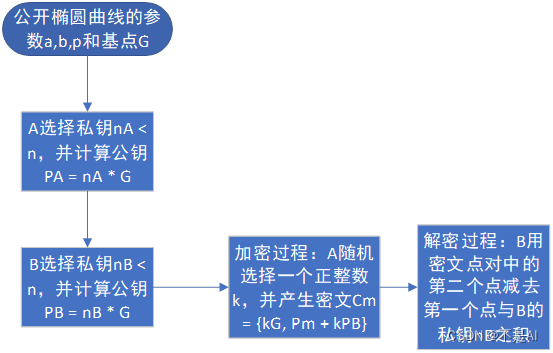
首先,将要发送的消息明文m编码为形为(x,y)的点Pm,并对点Pm进行加密和其后的解密。加/解密系统需要点G和椭圆群参数(p,a,b)。用户A悬念则一个私钥nA,并产生公钥PA = nA * G. A随机选择一个正整数k,并产生密文Cm,该密文时一个点对
Cm = {kG, Pm + kPB},其中PB为B的公钥。B在对密文解密时,则需用第二个点减去第一个点与B的私钥之积,得到消息Pm。
算法流程由下图简要表示:
三、算法实现
1、Python代码
文件1:ecc.py,定义椭圆曲线上的运算
文件内容:
# 加法
def add(xp, yp, xq, yq, a, b, p): # 计算(Zp上的)椭圆曲线上两点P(xp, yp)和Q(xq, yq)的和
if (4 * (a ** 3) + 27 * (b ** 2)) % p == 0:
print('不能形成abel群')
return
else:
if yp + yq == 0:
print('infinity')
return
else:
if (xp == xq) and (yp == yq):
delta = (3 * (xp ** 2) + a) * inverse((2 * yp), p) % p
xr = (delta ** 2 - xp - xq) % p
yr = (-yp + delta * (xp - xr)) % p
return xr, yr
else:
delta = (yq - yp) * inverse((xq - xp), p) % p
xr = (delta ** 2 - xp - xq) % p
yr = (-yp + delta * (xp - xr)) % p
return xr, yr
# 减法
def sub(xp, yp, xq, yq, a, b, p):
return add(xp, yp, xq, -yq, a, b, p)
# 乘法
def mul(n, xp, yp, a, b, p):
ans_x = xp
ans_y = yp
for i in range(0, n - 1):
(ans_x, ans_y) = add(ans_x, ans_y, xp, yp, a, b, p)
return ans_x, ans_y
# 求逆
def inverse(a, p):
for i in range(1, p):
if ((i * a) % p) == 1:
return i
# 除法
def div(n, xp, yp, a, b, p):
m = inverse(n, p)
return mul(m, xp, yp, a, b, p)
# 以下为测试
# print(add(-3, 9, -2, 8, 0, -36, 11))
# print(sub(10, 2, 3, 5, 1, 6, 11))
# print(mul(7, 8, 3, 1, 6, 11))
# print(inverse(2, 3))
# print(div(12, 3, 10, 1, 1, 23))
文件2:dh.py,用于产生公钥和私钥
文件内容:
from ecc import *
def generateKey_a(na, xg, yg, a, b, p):
(x_pa, y_pa) = mul(na, xg, yg, a, b, p)
return x_pa, y_pa
def generateKey_b(nb, xg, yg, a, b, p):
(x_pb, y_pb) = mul(nb, xg, yg, a, b, p)
return x_pb, y_pb
def secret_a(na, x_pb, y_pb, a, b, p):
(xka, yka) = mul(na, x_pb, y_pb, a, b, p)
return xka, yka
def secret_b(nb, x_pa, y_pa, a, b, p):
(xkb, ykb) = mul(nb, x_pa, y_pa, a, b, p)
return xkb, ykb
(xpa, ypa) = generateKey_a(121, 2, 2, 0, -4, 211)
(xpb, ypb) = generateKey_b(203, 2, 2, 0, -4, 211)
(xka, yka) = secret_a(121, xpb, ypb, 0, -4, 211)
(xkb, ykb) = secret_b(203, xpa, ypa, 0, -4, 211)
print('A的私钥:121')
print('B的私钥:203')
print('A的公钥:', xpa, ypa)
print('B的公钥:', xpb, ypb)
print('A产生的秘密钥: ', xka, yka)
print('B产生的秘密钥: ', xkb, ykb)
文件3:crypt.py,用于椭圆曲线加、解密
文件内容:
from dh import *
def encrypt(pm_x, pm_y): # 椭圆曲线加密
(x_pb, y_pb) = generateKey_b(101, 2, 2, 0, -4, 257)
k = 41
(cm1_x, cm1_y) = mul(k, 2, 2, 0, -4, 257) # Cm1 = kG
(temp_x, temp_y) = mul(k, x_pb, y_pb, 0, -4, 257)
(cm2_x, cm2_y) = add(temp_x, temp_y, pm_x, pm_y, 0, -4, 257)
return cm1_x, cm1_y, cm2_x, cm2_y
def decrypt(cm1_x, cm1_y, cm2_x, cm2_y): # 椭圆曲线解密
nb = 101
(tempx, tempy) = mul(nb, cm1_x, cm1_y, 0, -4, 257)
(pmx, pmy) = sub(cm2_x, cm2_y, tempx, tempy, 0, -4, 257)
return pmx, pmy
(cm1x, cm1y, cm2x, cm2y) = encrypt(112, 26)
(pmx, pmy) = decrypt(136, 128, 246, 174)
# (xpb, ypb) = generateKey_b(101, 2, 2, 0, -4, 257)
# print(xpb)
# print(ypb)
# (kpbx, kpby) = mul(41, xpb, ypb, 0, -4, 257)
# print(kpbx)
# print(kpby)
print('加密结果:')
print(cm1x)
print(cm1y)
print(cm2x)
print(cm2y)
print()
print('解密结果:')
print(pmx)
print(pmy)
2、运行测试
经运行,解密结果==明文。
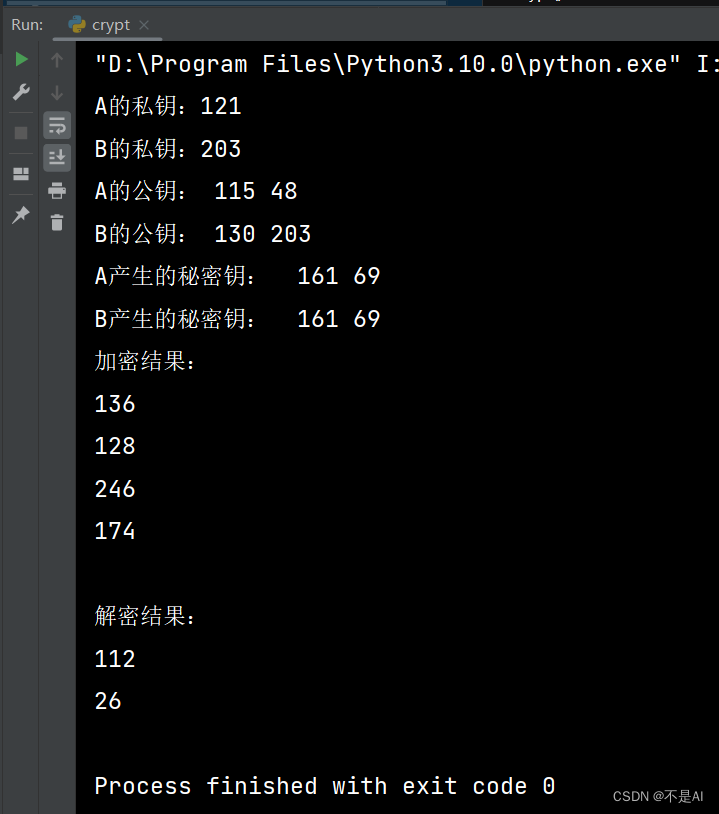
至此,本次实验结束。
四、参考文献
1、《密码编码学与网络安全——原理与实践(第七版)》(Cryptography and Network Security, Principles and Practice, Seventh Edition),【美】威廉 斯托林斯 William Stallings 著,王后珍等 译,北京,电子工业出版社,2017年12月。
2、《密码学实验教程》,郭华 刘建伟等 主编,北京,电子工业出版社,2021年1月。